Реальное течение пара или газа по каналам.

Рассмотренное выше движение газа (пара) по каналам различной формы происходило в условиях адиабатно-изоэнтропийного процесса (см. предпосылки построения термодинамической модели процесса течения). Это возможно в идеальных условиях отсутствия трения и теплообмена с внешней средой. В реальных течениях поток взаимодействует со стенкой канала, а высокая температура потока неизбежно ведет к теплопередаче с окружающей средой.

Последнее обстоятельство является предметом специального курса «Теплообмен», в рамках дисциплины «Процессы и аппараты химической технологии», и мы его касаться не будем.

Трение возникает по причине шероховатости внутренней поверхности канала и вязкости рабочего тела (свойство вещества). При движении по каналу в месте контакта с поверхностью поток полностью теряет скорость (w = 0), возникает профиль скорости по радиусу канала с максимумом на оси симметрии канала. В термодинамике такие детали не рассматриваются, а скорость потока принимается постоянной по радиусу и равной

w = 4Gv/πd² м/с,

где G – массовый расход среды кг/с, d – диаметр канала в данном сечении, м. И вся работа трения условно сносится на поверхность контакта потока со стенкой канала. Тогда схема термодинамической системы для реальных течений сводится к взаимодействию потока с окружающей средой, т.е. стенкой канала + атмосферой.

Для неподвижного канала (δl_технич = 0) применимо уравнение (5.1 – в)

du + d(w²/2) = δq – δl_потока – δl_трения (5.14)

Напомним, что работа трения полностью диссипирует, т.е. обращается в тепловую энергию, которую поток (а он не различает причину) воспринимает как подвод теплоты из окружающей среды: l_трения = q_трения.

Уравнение энергии потока без учета теплообмена получает следующий вид:

dw²/2 + dh + δl_трения = 0, (5.15)

и, если считать начальную скорость потока (на входе в канал) нулевой, то получаем

w = [2(h₁ – h_трения)]^1/2. (5.16)

В этой формуле величина энтальпии h_трения рассчитывается по эмпирическим данным следующим образом:

h_трения = h_s + Δ_трения, (5.17)

где h_s – величина энтальпии в конечной точке идеального процесса течения при s = const, а Δ_трения – потери энтальпии на работу трения. Эта величина рассчитывается как

Δ_трения = w²/2 (1 – φ²) = (h₁ – h₂)(1 – φ²). (5.18)

Здесь φ – коэффициент скорости, φ ≡ w_трения/w_s, является опытной или справочной величиной для данного канала.

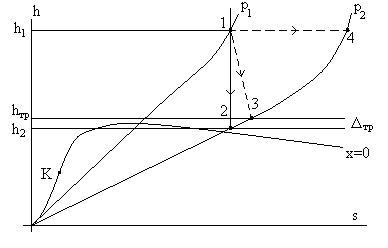
Рис. 5.14. Иллюстрация к расчету скорости в канале с учетом трения.

Из рис. 5.14 следует, что точка 3 находится на изобаре р₂ = const и она расположена правее точки 2 согласно 2 – му закону термодинамики (Δs_диссип = s₃ – s₂ > 0).