РІВНЯННЯ ЕЙНШТЕЙНА
Чітке пояснення фотоефекту дав А. Ейнштейн у 1905 р. на основі припущення, що світло є потоком матеріальних частинок – фотонів, енергія яких

Зазначимо, що на відміну від Планка, який вважав, що системи атомів і молекул мають властивість тільки випромінювати енергію квантами, а самі можуть мати будь-яку енергію і поглинати її в будь-якій кількості безперервно, Ейнштейн пішов далі, зробивши припущення, що світло поглинається такими самими порціями, якими воно випромінюється.
Таким чином, за теорією Ейнштейна, падаючий світловий потік визначається кількістю фотонів, що падають на поверхню тіла за одиницю часу; при цьому кожний фотон може взаємодіяти тільки з одним електроном.
З теорії Ейнштейна безпосередньо випливають закономірності фотоефекту. Безінерційність підтверджує, що електрони сприймають світлову енергію окремими порціями, завдяки чому виходять за межі металу. Чим більший світловий потік, тим більша кількість фотонів у ньому і при тій самій імовірності захоплення фотонів за 1 с буде вивільнятися більша кількість електронів. Зазначимо, що енергія переважної більшості падаючих фотонів розсіюється в тілі, перетворюється у внутрішню, і тільки близько 1% фотонів спричиняють вихід електронів; глибина активного в фотоелектричному відношенні шару на поверхні металу не перевищує сотні атомних діаметрів, тобто порядку 10-6 см.
Застосувавши до взаємодії фотона з електроном закон збереження енергії, Ейнштейн встановив рівняння фотоефекту
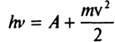 (1)
(1)
де: hv– енергія фотона;
А– робота виходу електрона з освітлюваного тіла;
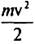 – надана електрону кінетична енергія.
– надана електрону кінетична енергія.
З рівняння Ейнштейна видно, що швидкість вилітаючих фотоелектронів буде тим більшою, чим більша частота падаючого світла, і вона не залежить від інтенсивності світла, бо ні А, ні hне залежать від інтенсивності світла. Цей висновок з рівняння цілком узгоджується з результатами дослідів.
З рівняння (1) також випливає, що зовнішній фотоефект можливий при частоті світла 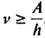 . Це означає, що для кожного тіла повинна існувати певна «червона межа» фотоефекту v0, яка задовольняє умову
. Це означає, що для кожного тіла повинна існувати певна «червона межа» фотоефекту v0, яка задовольняє умову
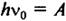 (2)
(2)
За значенням частоти “червоної межі”, виміряної дослідним шляхом, та умовою (2) було знайдено значення роботи виходу електронів з різних металів. Ці роботи виходу збіглися за величиною із значеннями, знайденими при вивченні явища термоелектронної емісії в тих же металах.
Було встановлено, що робота виходу електрона з платини становить 5,3 еВ, з цинку 4,2 еВ, цезію — 1,9 еВ і т. д.
Закони фотоефекту і рівняння Ейнштейна неодноразово перевірялися різними вченими. Найбільш точну експериментальну перевірку рівняння фотоефекту провели в 1928 р. П. І. Лукірський і С. С. Прилежаєв. На відміну від попередніх експериментаторів, які подібно до Столєтова, користувалися плоским конденсатором, вони використали для дослідження фотоефекту сферичний конденсатор. Зовнішнім електродом у ньому була посріблена внутрішня поверхня скляної кулі В(рис. 5), внутрішнім – кулька з досліджуваного металу К; остання освітлювалася через кварцове віконце О
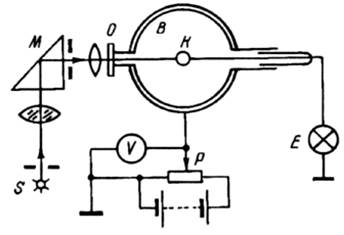
Рис. 5. Установка Лукірського і Прилежаева для дослідження фотоефекту
світлом певної довжини хвилі, яке діставали від ртутної дуги із наступним розкладанням у лінійчастий спектр за допомогою монохроматора М. Кулька Кз'єднувалася з квадрантним електрометром Е; всередині конденсатора створювався високий вакуум. Напруга між електродами конденсатора Ві змінювалася за величиною і знаком потенціометром Р.
Перевагою методу сферичного конденсатора є його висока чутливість. Оскільки електрод Вповністю охоплює кульку К, всі електрони, що вириваються з кульки, досягають електрода Вбез прискорюючої напруги (U = 0).Даний метод дає змогу дуже точно визначити гальмуючу напругу U2(див. рис. 4).
Досліди Лукірського і Прилежаєва підтвердили вірогідність законів фотоефекту і рівняння Ейнштейна.
Приклад.На поверхню цинку падає проміння з довжиною хвилі 
 λ= 2,47 нм. Визначити максимальну швидкість фотоелектронів, що вириваються з металу (робота виходу електрона з цинку А= 4,2 еВ).
λ= 2,47 нм. Визначити максимальну швидкість фотоелектронів, що вириваються з металу (робота виходу електрона з цинку А= 4,2 еВ).
Розв'язання. Скористаємось рівнянням Ейнштейна
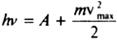
Щоб розв'язати рівняння Ейнштейна, треба з'ясувати, яку масу електрона слід врахувати – спокою чи релятивістську. Про це можна дізнатися, порівнявши енергію фотона з енергією спокою електрона: якщо енергія фотона значно менша від енергії спокою електрона, доцільно скористатися масою спокою, а якщо енергія фотона порівняна і більша за енергію спокою електрона, то – релятивістською масою електрона, тобто скористатися релятивістською формулою кінетичної енергії:
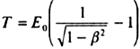
де 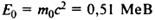 енергія спокою електрона; β = v/c.
енергія спокою електрона; β = v/c.
Обчислимо енергію фотона
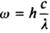 ;
; 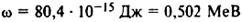 ; 0,502 МеВ = 0,51 МеВ.
; 0,502 МеВ = 0,51 МеВ.
Отже, треба користуватися релятивістською формулою кінетичної енергії електрона; роботою виходу електрона, яка є дуже малою порівняно з енергією фотона, можна знехтувати. Підставивши замість величини кінетичної енергії електрона значення енергії фотона, знаходимо:
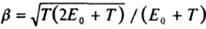
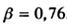
Шукана максимальна швидкість фотоелектронів становитиме:
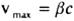
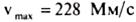
Дата добавления: 2015-08-21; просмотров: 2750;
