Описаний процес насправді не є хвилею, тобто цей процес – однократний, а не поширюється періодичним коливальним процесом.
Поширення у нас є, а от коливань немає . Але цей недолік дуже легко поправити . Змусимо ту ж силу, яка вивела електрон з первинного положення, відразу ж повернути його на місце. Тоді за першою перебудовою радіального електричного поля відразу піде друга, що відновлює початковий розподіл ліній електричного поля. Нехай тепер електрон періодично повторює цей рух, і тоді по радіальних силовим лініям електричного поля в усі сторони побіжать справжні хвилі. Ця картина вже багато краще першої. Втім , вона теж не цілком вірна - хвилі виходять чисто електричними, а не електромагнітними.
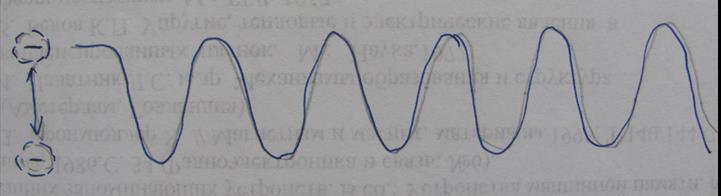
Тут саме час згадати про закон електромагнітної індукції: змінне електричне поле породжує змінне магнітне, а змінюється магнітне – виникає електричне. Ці два поля як би зчеплені один з одним. Як тільки ми створюємо хвилеподібну зміну електричного поля, так відразу ж до нього додається і магнітна хвиля . Розділити цю пару хвиль неможливо - це єдине електромагнітне явище .
Напрям векторів напруженості електричного і магнітного полів, а також напрям поширення електромагнітних хвиль взаємно перпендикулярні. Отже, електромагнітні хвилі – поперечні. На рис. 4.1 схематично зображено плоску електромагнітну хвилю. В цьому разі вектор напруженості електричного поля Εколивається у вертикальній площині zOx, а вектор напруженості магнітного поля Ηв горизонтальній площині yОх.
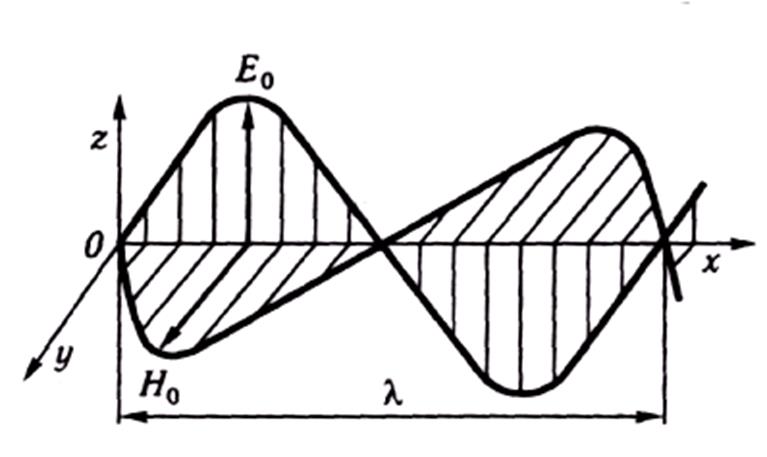 Рис. 4.1
Рис. 4.1
Аналізуючи закон електромагнітної індукції М. Фарадея, Дж. Максвелл висунув гіпотезу, що змінне в часі магнітне поле породжує вихрове електричне, тобто силові лінії електричного поля замкнені й охоплюють силові лінії магнітного поля. Щоб формально узгодити свою теорію із законом збереження заряду, Дж. Максвеллу довелось припустити, що не тільки змінне в часі магнітне поле породжує вихрове електричне, а й навпаки: змінне в часі електричне поле породжує вихрове магнітне поле.
Точний запис сформульованого закону містить додаткове припущення про так званий струм зміщення Із, який Дж. Максвелл визначив як (локальну) похідну по часу від вектора електричної індукції D
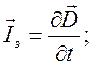
Цю гіпотезу покладено в основу одного з рівнянь Максвелла, що цілком узгоджується з експериментом.
Отже, за Максвеллом, змінне в часі електричне й магнітне поля породжують одне одного, і цей процес може поширюватися від точки до точки в просторі, збуджуючи електромагнітні хвилі.
Основою теорії є рівняння Максвелла. У вченні про електромагнетизм ці рівняння відіграють таку саму роль, як і закони Ньютона в механіці або основні закони (принципи) в термодинаміці. Рівнянням Максвелла підлягає поширення електромагнітних хвиль.
У диференціальній формі рівняння Максвелла набувають вигляду:
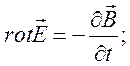
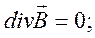
(4.1)
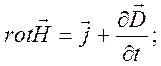
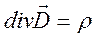
де В = μμ0Η, D = εε0Ε(ε0 і μ0 – електрична і магнітна сталі, ε і μ – відносні діелектрична
і магнітна проникності середовища),
j – густина струму провідності;
ρ – об'ємна густина електричних зарядів.
Для з'ясування основних закономірностей, що характеризують поширення електромагнітних хвиль, розглянемо поширення плоскої електромагнітної хвилі в однорідному непровідному середовищі (ρ = 0, j = 0).
Якщо вісь xнаправити перпендикулярно до хвильових поверхонь, то E і H, а отже, і їхні складові не залежатимуть від координат tта x, тому
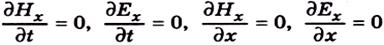
і рівняння (4.1) спрощуються:
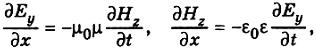 (4.2)
(4.2)
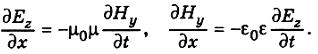 (4.3)
(4.3)
Отже, саме поле хвилі не має складової вздовж осі х, тобто вектори Ε і Ηперпендикулярні до напряму поширення хвилі. Рівняння (4.2) дають зв'язок між складовими Еуі Нz, а рівняння (4.3) зв'язують складові Еzі Ну.
Щоб описати плоску електромагнітну хвилю, досить взяти одну пару, наприклад, Еуі Нz. При цьому можна прийняти другу пару рівною 0: Еz = 0і Ну= 0.
Завдяки прийнятому припущенню можна використовувати тільки одну із систем рівнянь (4.2) та (4.3).
Описуючи хвилю, візьмемо першу групу рівнянь (4.2), поклавши Еz = Ηy = 0.
Якщо продиференціювати перше рівняння (4.2) по x і врахувати, що
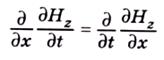
(це випливає із незалежності змінних x і t), то, підставивши потім 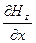 з другого рівняння, дістанемо хвильове рівняння для Εу:
з другого рівняння, дістанемо хвильове рівняння для Εу:
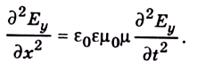 (4.4)
(4.4)
Диференціюючи по xдруге рівняння (4.2), матимемо після аналогічних перетворень хвильове рівняння для Нz:
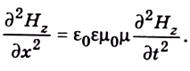 (4.5)
(4.5)
Оскільки інші складові ΕiΗдорівнюють нулю, то Ε = Εy Η = Ηz. Остаточно рівняння для плоскої електромагнітної хвилі матимуть такий вигляд:
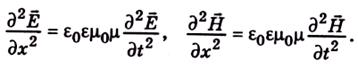 (4.6)
(4.6)
Отже, обидва компоненти електромагнітного поля Ε і Ηописуються однаковим диференціальним рівнянням. Процеси, які описуються рівняннями (4.6), мають хвильовий характер. Зокрема, розв'язком рівняння (4.6) для складової електричного поля є така функція:
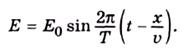 (4.7)
(4.7)
Цей вираз є рівнянням плоскої біжучої хвилі, що поширюється вздовж позитивного напрямку осі xз амплітудою Ео, періодом коливань Τі швидкістю поширення υ.
Якщо позначити
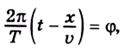
то рівняння (4.7) можна записати так:
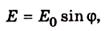 (4.8)
(4.8)
де φ - фаза хвилі.
Якщо розглядати хвильовий процес у будь-якій точці простору в залежності від часу, то ми маємо покласти x= const і вважати змінною лише величину t. Для спрощення покладемо x= 0. Тоді фаза залежатиме від часу:
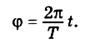 (4.9)
(4.9)
Визначимо проміжок часу 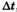 , за який φ змінюється на 2π, а Е повторює своє значення, що відповідає моменту t. Скориставшись співвідношенням (4.9), маємо
, за який φ змінюється на 2π, а Е повторює своє значення, що відповідає моменту t. Скориставшись співвідношенням (4.9), маємо
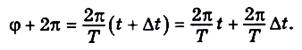 (4.10)
(4.10)
Звідси випливає, що зміна фази на величину 2π відбувається за 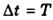 . Отже, напруженість електричного поля повторює свої значення в даній точці простору через проміжки часу Т, тобто Τє періодом коливаньвектора напруженості електричного поля Е.
. Отже, напруженість електричного поля повторює свої значення в даній точці простору через проміжки часу Т, тобто Τє періодом коливаньвектора напруженості електричного поля Е.
На рис. 4.2 зображено залежність вектора напруженості електричного поля Εвід часу.
І 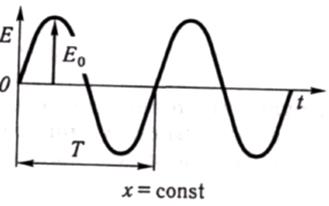
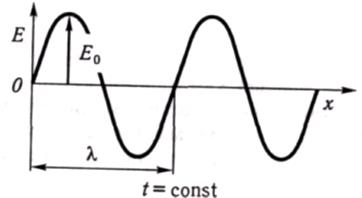
Рис. 4.2 Рис. 4.3
Можна графічно зобразити стан процесу в певний момент часу t = const, наприклад при t = t0, то утворений графік буде подібним до графіка на рис. 4.2, але змінною величиною в цьому разі стане координата х. Графік показує миттєве положення хвиль у момент часу t = t0 (рис. 4.3).
Період (по координаті) зміни напруженості електричного поля Εв просторі можна знайти з таких умов. У точці xпри t = t0 фаза матиме значення 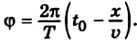 . Більш віддалені точки хвилі відповідатимуть більш раннім моментам проходження їх через точку x= 0. Нехай на відстані
. Більш віддалені точки хвилі відповідатимуть більш раннім моментам проходження їх через точку x= 0. Нехай на відстані 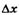 від точки x фаза зміниться на 2π, тобто дорівнюватиме φ-2π. Тоді
від точки x фаза зміниться на 2π, тобто дорівнюватиме φ-2π. Тоді 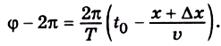 Звідси, враховуючи, що
Звідси, враховуючи, що 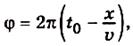 дістанемо
дістанемо
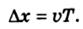 (4.11)
(4.11)
Оскільки при зміні φ на 2π вектор Εздійснює повне коливання, то величина 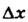 є періодом зміни функції Εв просторі й називається довжиною хвилі. Цю величину позначають літерою λ. Довжину хвилі можна виразити через швидкість її поширення і період коливань:
є періодом зміни функції Εв просторі й називається довжиною хвилі. Цю величину позначають літерою λ. Довжину хвилі можна виразити через швидкість її поширення і період коливань:
λ = uΤ (4.12)
Дата добавления: 2015-08-21; просмотров: 790;
