Первое достаточное условие локального экстремума

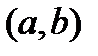Теорема 1 (первое достаточное условие локального экстремума). Пусть функция определена на и дифференцирована на этом интервале везде за исключением, возможно, точки 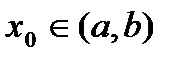, но в этой точке 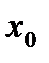функция является непрерывной. Если существуют такие правая и левая полуокрестности точки 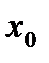, в каждой из которых 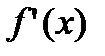сохраняет определенный знак, то

1) функция имеет локальный экстремум в точке 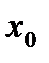, если 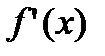принимает значения разных знаков в соответствующих полуокрестностях;

2) функция не имеет локальный экстремум в точке 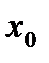, если справа и слева от точки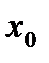 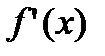имеет одинаковый знак.

Доказательство. 1) Предположим, что в полуокрестности 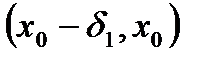производная 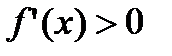, а в .

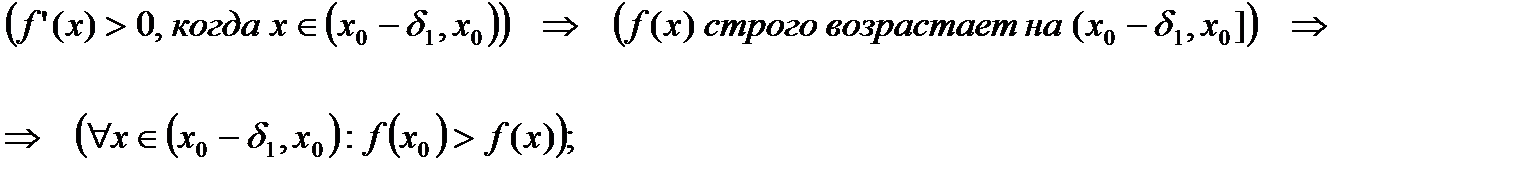
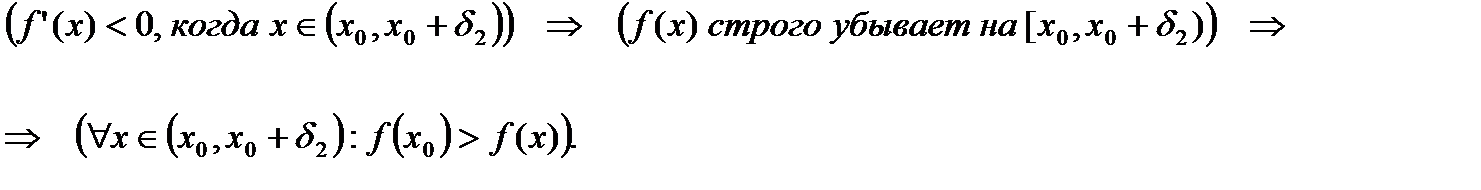
Таким образом в точке 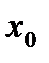функция имеет локальный экстремум, а именно - локальный максимум, что и нужно было доказать.

2) Предположим, что слева и справа от точки 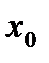производная сохраняет свой знак, например, 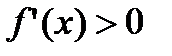. Тогда на 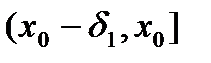и 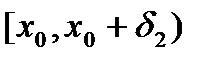функция строго монотонно возрастает, то есть:

,

.

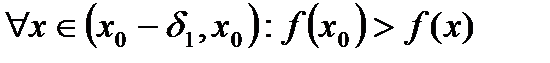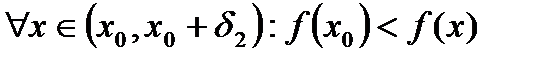Таким образом экстремума в точке 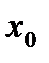функция не имеет, что и нужно было доказать.

Замечание 1. Если производная 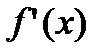при прохождении через точку 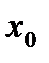меняет знак с «+» на «-», то в точке 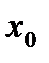функция имеет локальный максимум, а если знак меняется с «-» на «+», то локальный минимум.

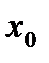Замечание 2. Важным является условие непрерывности функции в точке . Если это условие не выполняется, то теорема 1 может не иметь места.

Пример. Рассматривается функция (рис.1):

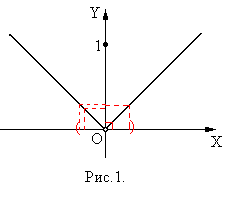
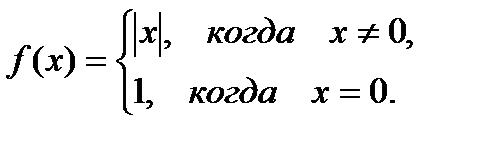
Эта функция определена на 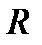и непрерывна везде, кроме точки 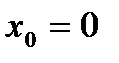, где она имеет устранимый разрыв. При прохождении через точку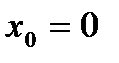 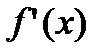меняет знак с «-» на «+», но локального минимума в этой точке функция не имеет, а имеет локальный максимум по определению. Действительно, около точки 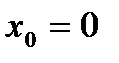можно построить такую окрестность, что для всех аргументов из этой окрестности значения функции будут меньше, чем значение 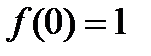. Теорема 1 не сработала потому, что в точке 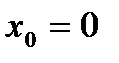функция имела разрыв.

Замечание 3. Первое достаточное условие локального экстремума не может быть использовано, когда производная функции 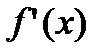меняет свой знак в каждой левой и каждой правой полуокрестности точки .

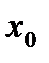Пример. Рассматривается функция:

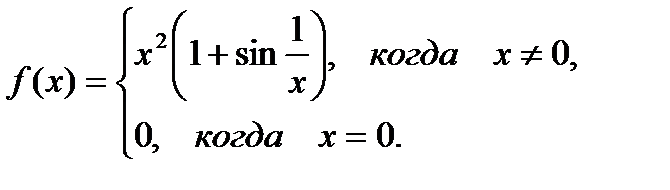
Поскольку 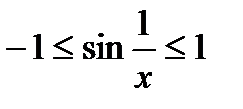, то 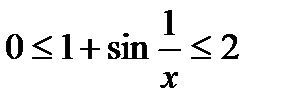, а потому 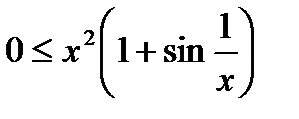, но . Таким образом:

,

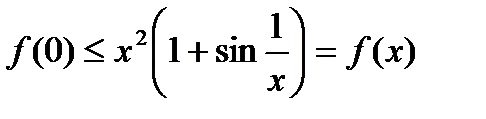т.е. в точке 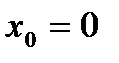функция имеет локальный минимум по определению. Посмотрим, сработает ли здесь первое достаточное условие локального экстремума.

Для :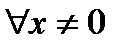

.

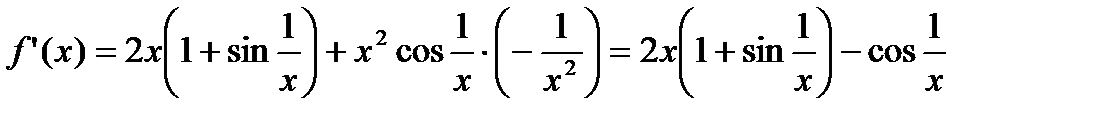Для первого слагаемого правой части полученной формулы имеем:

,

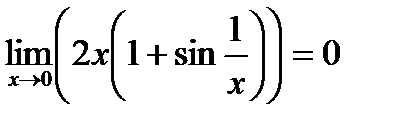а потому в малой окрестности точки 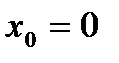знак производной определяется знаком второго слагаемого, то есть:

,

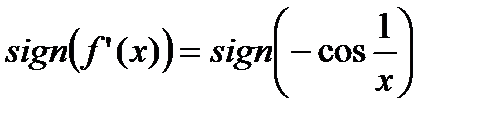а это означает, что в любой окрестности точки 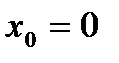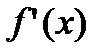будет принимать как положительные, так и отрицательные значения. Действительно, рассмотрим произвольную окрестность точки 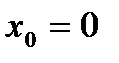: 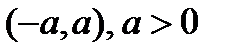. Когда

,

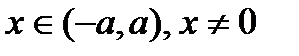то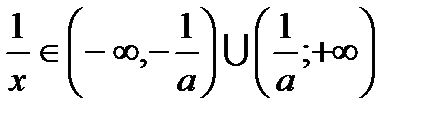

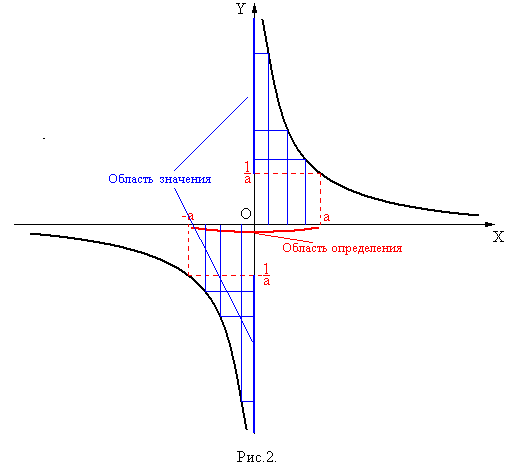
(рис.2), а 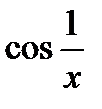меняет свой знак здесь бесконечно много раз. Таким образом, нельзя использовать в приведенном примере первое достаточное условие локального экстремума.