Односторонние производные

Пусть функция определена на полусегменте .

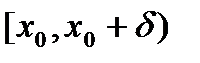Определение 2. Если существует

,

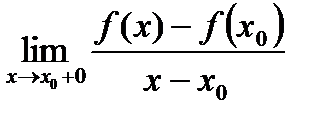он называется правосторонней производной функции в точке 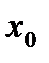и обозначается .

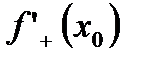Пусть функция определена на полусегменте .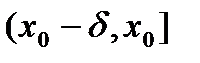

Определение 3. Если существует

,

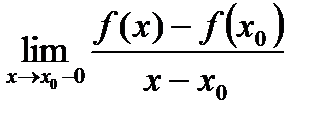он называется левосторонней производной функции в точке 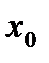и обозначается .

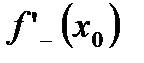Теорема 1 (критерий дифференцированности функции в точке). Для того, чтобы функция была дифференцирована в точке 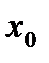необходимо и достаточно, чтобы в этой точке существовал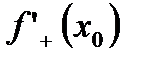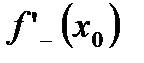и , и

.

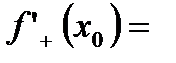
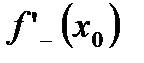Задание. Доказать теорему 1.

Пример. Доказать, что функция 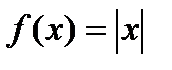не имеет производной в точке .

,

.

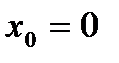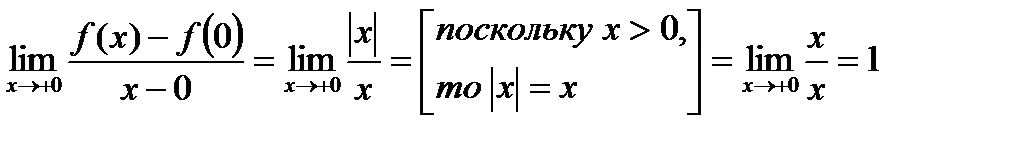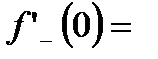
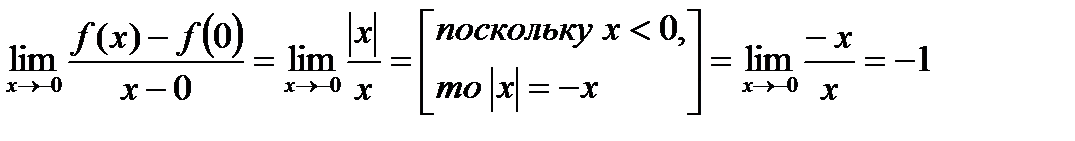Поскольку 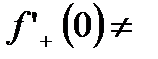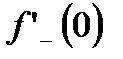, то функция 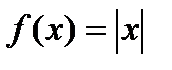не имеет производной в точке .

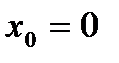Теорема 2. Если функция дифференцирована в точке 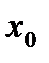, то она непрерывна в этой точке.

Доказательство. Поскольку дифференцирована в точке 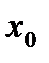, то в достаточно малой окрестности точки 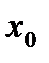для нее имеет место равенство (5):

.

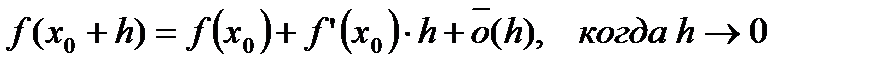Перейдем к пределу в последнем равенстве, когда :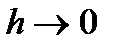

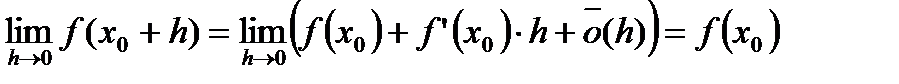. (6)

Вспомним, что 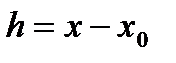, тогда (6) имеет вид:

,

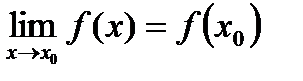что свидетельствует о непрерывности функции в точке .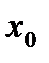

Замечание. Из непрерывности функции в точке 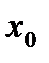вообще не вытекает ее дифференцированность в этой точке. Например, функция 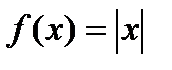непрерывна в точке 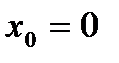, но не имеет в этой точке производной.

Определение 4. Пусть функция определена в некоторой окрестности точки 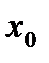. Если

,

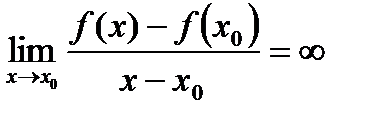то говорят, что имеет бесконечную производную в точке .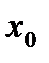

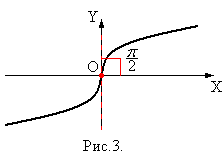
Пример. Рассматривается функция 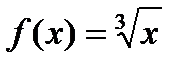(рис.3).

.

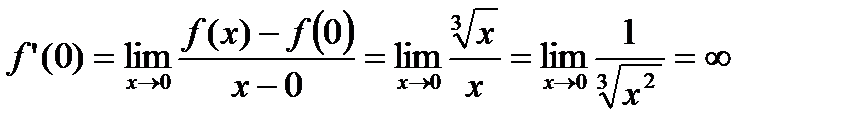Замечание. Существование у функции бесконечной производной не обеспечивает непрерывности функции в этой точке.

Пример. Рассматривается функция .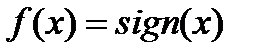

,

.

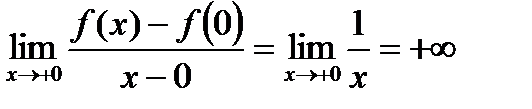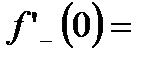
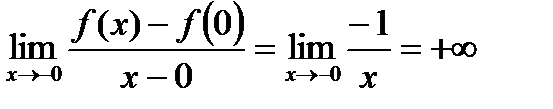Таким образом, , а функция 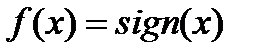имеет в точке 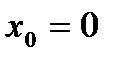разрыв І рода.