Моделирование нормального распределения
Будем обозначать через 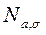 - случайную величину, распределенную по нормальному закону с плотностью
- случайную величину, распределенную по нормальному закону с плотностью
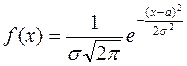
Если а=0, 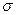 =1, то говорят о стандартной нормальной случайной величине, которую обозначим N. Связь между
=1, то говорят о стандартной нормальной случайной величине, которую обозначим N. Связь между 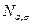 и N простая:
и N простая:
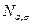 =a+
=a+ 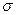 N
N
Поэтому достаточно имитировать N. Разработаны многочисленные способы имитации этой величины. Рассмотрим некоторые из них.
Метод полярных координат.
Утверждение. Пусть Х и У независимые случайные величины со стандартным нормальным распределением. Рассмотрим случайную точку на плоскости - (Х,У) и ее полярные координаты 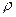 и
и 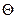 :
:
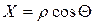
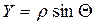 (9.1)
(9.1)
Тогда 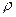 и
и 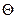 будут независимыми случайными величинами, распределенными по следующим законам:
будут независимыми случайными величинами, распределенными по следующим законам:
- имеет функцию распределения 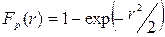
- распределена равномерно на [0,2 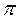 ].
].
Наоборот, если 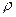 и
и 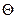 имеют указанные распределения и независимы, то величины Х и У, вычисленные по формулам (9.1), независимы и имеют стандартное нормальное распределение. Доказательство очевидно из следующих преобразований:
имеют указанные распределения и независимы, то величины Х и У, вычисленные по формулам (9.1), независимы и имеют стандартное нормальное распределение. Доказательство очевидно из следующих преобразований:
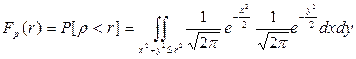 =
= 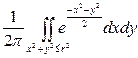 = =
= = 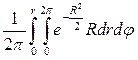 =
= 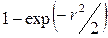
И обратно
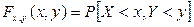 =
= 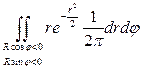 =
= 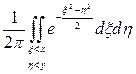 = =
= = 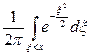
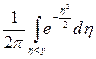
Рассмотрим способ имитации. Используя метод обратной функции, получим
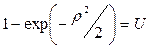 Откуда
Откуда 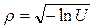
Полярный угол 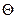 получается по формуле
получается по формуле 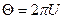 . Окончательно алгоритм имитации будет следующий
. Окончательно алгоритм имитации будет следующий
- от ДСЧ получаем 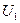 и
и 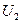 .
.
- вычисляем сразу пару значений N :
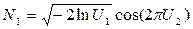 ,
, 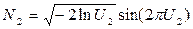 .
.
Приведенный метод имитации N является точным, легко программируется и точно работает. Известен как метод Бокса и Маллера.
Известна модификация этого метода, дающая точные результаты быстрее. По этому методу генерируются два случайных числа 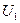 и
и 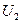 . Далее полагая
. Далее полагая 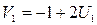 и
и 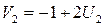 , вычисляют
, вычисляют 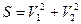 . При
. При 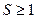 начинают цикл снова. При S<1 вычисляют
начинают цикл снова. При S<1 вычисляют
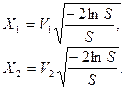
Дата добавления: 2015-08-21; просмотров: 1347;
