Применение интерференции. 1. С помощью колец Ньютона можно определить длину волны, если известен радиус кривизны плосковыпуклой линзы ( ).

1. С помощью колец Ньютона можно определить длину волны, если известен радиус кривизны плосковыпуклой линзы ( ).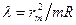

2. Явление интерференции применяется для улучшения качества оптических приборов (просветление оптики). Прохождение света через линзу сопровождается отражением 4% падающего света. Современные объективы содержат до 10 линз, поэтому потери света велики. Отражение от поверхности линз приводит к возникновению бликов, что приводит к демаскировке расположения приборов в военной технике. Для устранения этих недостатков осуществляют просветление оптики. Объектив покрывают пленкой. Ее толщину рассчитывают так, чтобы был интерференционный минимум при наложении лучей (рис. 5).

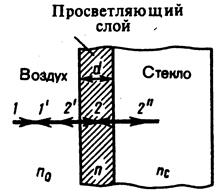Рис.5.

Оптическая разность хода между лучами 1 и 2 равна 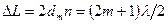. Слагаемое 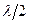отсутствует, так как оба луча отражаются от более плотных поверхностей ( 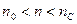). Пленка имеет наименьшую толщину при 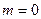. Она равна: 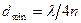. Толщину 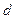подбирают так, чтобы гасить лучи наиболее сильно действующие на глаз (желто-зеленые). Объективы имеют фиолетовый оттенок.

Лекция 4.
Дифракция света

Дифракция света – это явление отклонения волн от прямолинейного распространения, явление огибания волнами препятствий и проникновения волн в область геометрической тени. Дифракция наблюдается, когда длина волны соизмерима с отверстиями или препятствиями. Например, звуковая волна - дифрагирует при прохождении сквозь окна и двери.

1. Принцип Гюйгенса – Френеля.

Явление дифракции объясняется с помощью принципа Гюйгенса, согласно которому каждая точка волновой поверхности становится источником вторичных волн, а огибающая этих волн дает положение волнового фронта в следующий момент времени.

Рис.1

В середине фронт волны будет плоский, на краях - загибается и заходит в область геометрической тени (рис.1).

Принцип Гюйгенса дает только геометрическое построение волны, но ничего не говорит об интенсивности волн, то есть об амплитуде.

Френель дополнил принцип Гюйгенса:

1. вторичные волны, испускаемые фиктивными источниками, когерентны и поэтому интерферируют в любой точке пространства.

2. вторичные волны испускаются только в направлении распространения волны, в обратном направлении не излучаются.

3. равные по площади участки волновой поверхности испускают равные мощности вторичного излучения.

Принцип Гюйгенса – Френеля это не законы, а метод рассмотрения явления дифракции. Этот метод можно проверить на опыте.

Дифракция света сводится к сложной математической задаче об интерференции от многих источников.

Различают два случая дифракции света: дифракцию Френеля, или дифракцию в сходящихся лучах, и дифракцию Фраунгофера, или дифракцию в параллельных лучах.

В случае дифракции Френеля на препятствие падает сферическая или плоская волна, а дифракционная картина на экране, находящемся за препятствием. В случае дифракции Фраунгофера на препятствие падает плоская волна, а дифракционная картина наблюдается на экране, который находится в фокальной плоскости линзы, установленной на пути прошедшего через препятствие света.

При дифракции Френеля на экране получается дифракционное изображение препятствия, а при дифракции Фраунгофера - дифракционное изображение удаленного источника света.

Метод зон Френеля. Прямолинейное распространение света.

С помощью принципа Гюйгенса – Френеля можно обосновать с волновой точки зрения закон прямолинейного распространения света в однородной среде. Френель рассмотрел интерференцию вторичных волн, используя метод зон Френеля.

Пусть свет распространяется от точечного источника 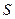в однородной среде. Найдем в произвольной точке 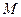амплитуду световой волны (рис.2).

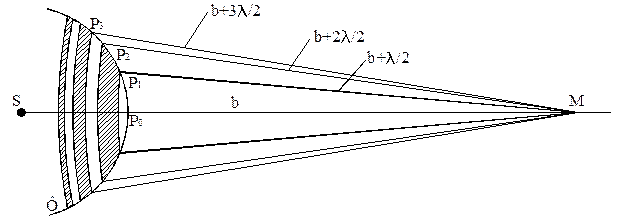Рис.2

Рассмотрим фронт волны 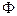, идущий от источника 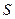. Это сферическая поверхность радиуса 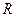с центром в точке 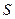. Согласно принципу Гюйгенса – Френеля, каждая точка волновой поверхности становится источником вторичных волн. Френель разбил волновую поверхность на зоны так, что расстояние от двух соседних зон для соответствующих точек до точки 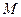отличались на 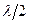. Подобное разбиение фронта волны на зоны можно выполнить, проведя с центром 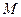окружности радиусами 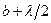, , 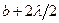, 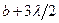…, 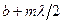. Колебания, возбуждаемые в точке 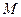двумя соседними зонами противоположны по фазе и при наложении будут ослаблять друг друга. Поэтому амплитуда результирующего колебания в точке 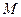будет равна:

.

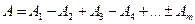(1)

С увеличением расстояния зоны от точки 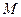амплитуда 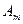уменьшается, поэтому .

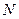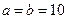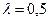Общее число зон Френеля очень велико (при см и мкм 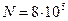). Поэтому амплитуды соседних зон близки по величине. Тогда амплитуда 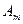от 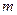зоны Френеля равна среднему арифметическому от амплитуд примыкающих к ней зон:

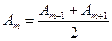
(2)

Тогда выражение (1) можно представить в виде:

.

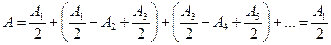Так как в силу (2) выражения в скобках равно нулю. Оставшаяся часть амплитуды от последней зоны 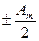ничтожна мала. Итак, амплитуда результирующих колебаний в точке 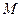определяется действием половины центральной зоны Френеля.

Найдем выражение для радиуса m-ой зоны Френеля.

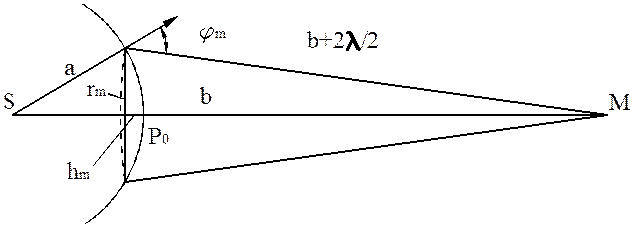Рис.3

Из рисунка 3 видно, что

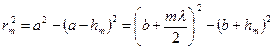
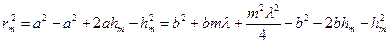
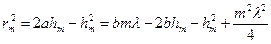
Так как 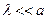и 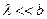, то членом можно пренебречь. В результате получаем:

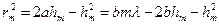
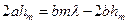
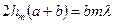
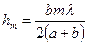
При не слишком больших значениях 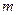высота шарового сегмента 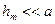, тогда 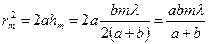, отсюда .

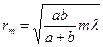Пр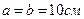и и 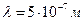радиус первой (центральной) зоны .

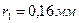Следовательно, в свободном пространстве свет от источника 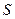в точку 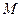распространяется по очень узкому каналу вдоль 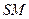, то есть прямолинейно.

Правомерность деления волнового фронта на зоны Френеля подтверждена экспериментально. Для этого используются зонные пластинки – стеклянные пластинки, состоящие из системы чередующихся прозрачных и непрозрачных концентрических колец, построенных по принципу расположению зон Френеля. Такая пластинка перекрывает четные зоны и оставляет свободными нечетные. Результирующая амплитуда 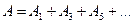будет больше, при полностью открытом фронте 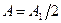. Зонная пластинка увеличивает освещенность в точке , действуя подобно собирающей линзе.