Тонкие линзы. Изображение предметов с помощью собирающей линзы.

Виды линз. Главная оптическая ось линзы.

Линзой называется прозрачное для света стекло, ограниченное двумя сферическими поверхностями (одна из поверхностей может быть плоской). Линзы, у которой середина толще, чем края, называются выпуклыми, а те, у которых края толще середины – вогнутыми. Выпуклая линза является собирающей, а вогнутая – рассеивающей. Различные виды линз показаны на рис.3: 1 – двояковыпуклая, 3 – двояковогнутая, 2 – плосковыпуклая, 4 – плосковогнутая, 5 – выпукловогнутая, 6 – вогнутовыпуклая.

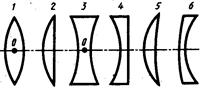Рис. 3.

Прямую 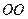, проходящую через центры сферических поверхностей, ограничивающих линзу, называют главной оптической осью линзы.

Оптический центр линзы. Побочные оптические оси.

Линзу, у которой толщина пренебрежимо мала по сравнению с радиусами кривизны поверхностей линзы и расстоянием от предмета до линзы называют тонкой. В тонкой линзе вершины шаровых сегментов расположены на столько близко, что их можно принять за одну точку. Эту лежащую на главной оптической оси точку 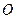, через которую световые лучи проходят не изменяя своего направления, называют оптическим центром тонкой линзы. Любую прямую, проходящую через оптический центр линзы называют оптической осью. Все оптические оси, кроме главной, называют побочными оптическими осями.

Главные фокусы и фокусные расстояния линзы.

Точку 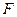на главной оптической оси, в которой пересекаются после преломления лучи, падающие на линзу параллельно главной оптической оси, называют главным фокусом линзы (рис. 4, рис. 5). Любая линза имеет два главных фокуса, расположенные по обе ее стороны симметрично оптическому центру.

У собирающей линзы (рис. 4) фокусы действительны, а у рассеивающей (рис. 5) –мнимые. Расстояние 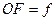от оптического центра линзы до ее главного фокуса называют фокусным. У собирающей линзы фокусное расстояние считают положительным, а у рассеивающей – отрицательным.

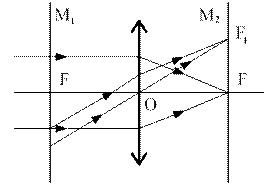Рис.4 Собирающая линза

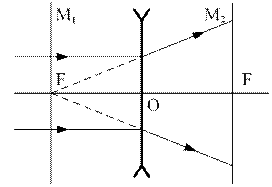Рис.5 Рассеивающая линза

Фокальные плоскости линзы и их свойства.

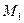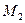Плоскости, проходящие через главный фокус тонкой линзы перпендикулярно главной оптической оси, называются фокальными. У каждой линзы две фокальные плоскости ( и на рис. 4 и 5), расположенные по обе стороны от линзы.

Лучи света, падающие на собирающую линзу параллельно какой-либо ее побочной оптической оси, после преломления в линзе сходятся в точке пересечения этой оси с фокальной плоскостью (в точке 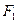на рис.4). Эту точку называют побочным фокусом.

Фокусное расстояние и оптическая сила линзы.

Величина 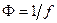называется оптической силой линзы. Чем больше 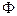, тем меньше фокусное расстояние , и, следовательно, тем сильнее преломляются лучи.

За единицу оптической силы принимают оптическую силу такой линзы, фокусное расстояние которой равно 1м. Эту единицу называют диоптрией ( ).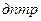

.

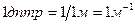Собирающие линзы имеют положительную оптическую силу, рассеивающие – отрицательную.

Вывод формулы тонкой линзы на основе геометрического построения хода лучей.

Пусть перед собирающей линзой находится светящийся предмет 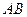(рис. 6). Для построения изображения этого предмета необходимо построить изображения его крайних точек, причем выбирать такие лучи, изображение которых окажется наиболее простым. Таких лучей, в общем случае, может быть три:

1. луч 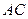, параллельный главной оптической оси, после преломления проходит через главный фокус линзы, то есть идет по прямой .

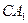2. луч 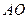, идущий через оптический центр линзы, не преломляется и тоже приходит в точку .

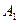3. луч 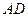, идущий через передний фокус линзы, после преломления идет параллельно главной оптической оси по прямой .

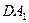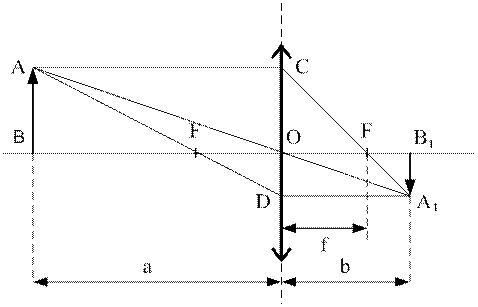Рис.6.

Все три указанных луча пересекаются в точке 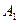, где получается действительное изображение точки 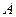. Опустив перпендикуляр на главную оптическую ось, находим точку 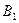, являющуюся изображением точки 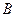. Для построения изображения достаточно двух из перечисленных лучей.

Используя рис. 6 выведем формулу тонкой линзы. Из подобия треугольников 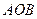и 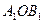следует соотношение 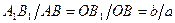. Из подобия треугольников 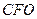и 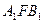следует 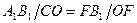. Так как 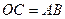, то 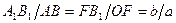. Поскольку 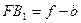, а 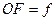, то последнюю формулу можно переписать в следующем виде: 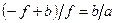. Упрощая это выражение, получаем формулу:

.

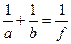Это выражение называется формулой тонкой собирающей линзы. У рассеивающей линзы фокусное расстояние отрицательное 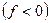, поэтому формула тонкой рассеивающей линзы имеет вид:

.

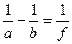Лекция 2
Волновая оптика