Принципи роботи спектрографа: його оптична схема, робота та призначення окремих вузлів
Спектрограф – спектральний прилад, у якому приймач випромінювання одночасно реєструє весь можливий електромагнітний спектр. Приймачами випромінювання можуть бути фотоматеріали, багатоелементні фотоприймачі, електронно-оптичні перетворювачі. Диспергувальна система (система, що поділяє потік випромінювання залежно від довжини хвилі) може бути призмою, дифракційною граткою тощо.
Оптична схема призмового спектрографа. Принципова схема призмового спектрографа наведена на рис. 4.5. Спектрограф має три основні частини: коліматор, що складається з об'єктиву 2 з фокусною відстанню f1 і щілини 1, встановленою у фокусі об'єктиву; диспергуючу систему 3, що складається з однієї або декількох заломлюючих призм; і камеру, що складається з об'єктиву 4 з фокусною відстанню f2 і фотопластини 5, розташованою у фокальній площині об'єктиву. Показник заломлення матеріалу призми не однаковий для різних довжин хвиль: n=n(l). Тому неоднорідний за спектральним складом паралельний пучок променів, що формується коліматором і що падає на призму, розбивається в ній на монохроматичні пучки за різними напрямами. Камерний об'єктив 4 збирає ці пучки у своїй фокальній площині, створюючи на фотопластині 5 послідовність монохроматичних зображень щілини – спектральні лінії. У своїй сукупності останні утворюють спектр досліджуваного джерела світла.
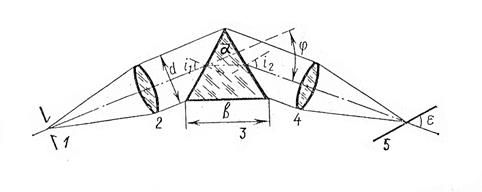
Рис. 4.5. Оптична схема призмового спектрографа: 1 – вхідна щілина,
2 – об'єктив коліматора, 3 – призма, 4 – камерний об'єктив, 5 – фотопластина,
d – діючий отвір приладу, b – довжина основи призми, j – кут відхилення променя призмою
Дисперсія спектрографа.Залежність кута відхилення j призмою монохроматичного променя від кута падіння i1 (рис. 4.5.) наступна: за умови i1=i2 кут j набуває найменшого значення. При постійному куті падіння кут відхилення немонохроматичного променя залежить від довжини хвилі: j=j(l). Величина dj/dl=(dj/dn)(dn/dl), відповідає постійному куту падіння i1, називається кутовою дисперсією призми. При рівності кута падіння куту заломлення (i1=i2), мінімальному значенні j для кутової дисперсії, має місце співвідношення:
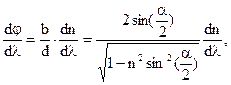 (4.9)
(4.9)
де b – довжина її основи на об'єктив 2 (при повному заповненні призми світлом);
d – проекція її грані на об'єктив 2 (при повному заповненні призми світлом);
l – заломлюючий кут призми.
Залежність n(l) обмеженої ділянці спектру можна розрахувати за наближеною формулою Гартмана:
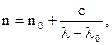 (4.10)
(4.10)
де n0, c, l0 – три константи при умові трьох довжин хвиль l1, l2, l3 відомі показники заломлення n1, n2, n3.
Значення dn/dl в (4.9) визначається диференціюванням (4.10).
Дисперсія показника заломлення (dn/dλ), а значить і дисперсія призми швидко збільшується зі зменшенням довжини хвилі. У короткохвильовій зоні робочого діапазону спектрографа дисперсія найбільша. Проте, інтенсивність спектральних ліній зменшується до нуля внаслідок сильного поглинання випромінювання речовиною призми. Зі збільшенням довжини хвилі дисперсія у видимій області спектру зменшується.
Лінійною дисперсією спектрографа називається величина дисперсії показника заломлення, що визначає лінійну відстань у фокальній площині приладу, яка доводиться на одиничний спектральний інтервал. Лінійна дисперсія пов'язана з кутовою співвідношенням:
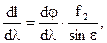 (4.11)
(4.11)
де f2 – фокусна відстань камерного об'єктиву 4 для цієї довжини хвилі;
e – кут нахилу його фокальної площини до оптичної осі об'єктиву (рис. 4.5).
При практичних розрахунках замість (4.11) використовується зворотна лінійна дисперсія dl/dl.
Роздільна здатність спектрографа. Спектральний прилад відображує строго монохроматичне випромінювання, освітлююче вхідну щілину, у вигляді деякого розподілу освітленості. Цей розподіл називають інструментальним контуром спектральної лінії або апаратною функцією. Її тип визначається спільною дією різних чинників. До їх числа належить дифракція на діючому отворі спектрографа (діючим отвором d є найменший з отворів (об'єктиву коліматора, призми або камерного об'єктиву), яке обмежує розміри перерізу паралельного пучка монохроматичних променів, що проходять через оптичну систему спектрографа (рис. 4.5)), різна аберація та інші похибки оптики приладу, ширина вхідної щілини і зерниста структура фотографічної емульсії. Форма інструментального контура лінії в основному визначається його дією.
Окремі ділянки інструментального контура якої-небудь лінії вносять формують контури інших ліній. Таким чином, монохроматичні складові початкового випромінювання утворюють кожний елемент реального контура лінії у спектрі. Таким чином, спектр на виході приладу складають дві функції – істинний розподіл енергії в джерелі та апаратна функція приладу. Спектральний прилад не завжди здатний передати два однакових за довжиною хвилі випромінювання у вигляді окремих спектральних ліній. Інструментальні контури таких ліній перекриваються. При цьому прилад не має дві близькі спектральні лінії.
Для оцінки можливостей приладу створювати окремо спектральні лінії близьких за довжиною хвилі враховують роздільну здатністю (дозволяючу силу):
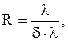 (4.12)
(4.12)
де d×l – межа дозволу приладу, що визначається шириною інструментального контура лінії.
В результаті дифракції монохроматичного паралельного пучка на діючому отворі прямокутної форми (на призмі) спектральна лінія має форму, показану на рис. 4.6, а.
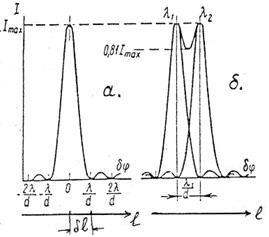
Рис. 4.6. Розподіл інтенсивності світла у фокальній площині приладу, що виникає в результаті дифракції на діючому отворі прямокутної форми для нескінченно вузької щілини спектрографа: а) поодинока монохроматична спектральна лінія; б) дві близькі монохроматичні лінії
Межу дозволу d×l можна розрахувати за критерієм Релея, згідно з яким дві спектральні лінії рівної інтенсивності є дозволеними при головному дифракційному максимумі інтенсивності однієї лінії, що співпадає з першим мінімумом (рис. 4.6, б). Кутова відстань від першого мінімуму до центру дифракційної картини дорівнює 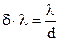 (кут дифракції малий при d>>l). Записавши для d j його вираз через кутову дисперсію
(кут дифракції малий при d>>l). Записавши для d j його вираз через кутову дисперсію 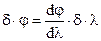 , отримуємо
, отримуємо 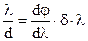 . Тому теоретичне значення для дозволяючої сили призми складає
. Тому теоретичне значення для дозволяючої сили призми складає
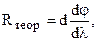 (4.13)
(4.13)
Таким чином, Rтеор пропорційна d, її максимальне значення досягається при заповненні діючого отвору приладу світлом.
При симетричного ході променів через призму для величини Rтеор можна отримати формулу
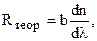 (4.14)
(4.14)
Реальне значення роздільної здатності Rпр менше Rтеор. Воно обмежується вказаними вище чинниками і може бути розраховане за формулою (4.12), де замість d l використовується Dlпр – практична межа дозволу, тобто різниця довжин хвиль двох близьких ліній з провалом інтенсивності між ними 20%.
Дозволяюча сила зменшується із збільшенням ширини вхідної щілини s1. Для дуже вузької щілини, коли її кутовий розмір s1/f1 менше кута dj =l /d, тобто s1<f1l/d, форма інструментального контура ще мало відрізняється від зображеної на рис. 4.6, а. Із зростанням s1 лінія розширюється і при s1>>f1l /d отримують щілини з геометричним зображенням, ширина якого рівна s2=s1f2/(f1sine). Граничною між цими двома випадками є нормальна ширина щілини sн. Визначимо її. Знайдемо таку величину вхідної щілини, коли її геометричне зображення у фокальній площині приладу дорівнює ширині центральної частини головного дифракційного максимуму в цій же площині. Для цього прирівняємо лінійну відстань від центру дифракційної картини до її першого нуля (рис. 4.6, а) величині геометричного зображення щілини sf2/f1. Звідси знаходимо
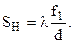 (4.15)
(4.15)
Ширина зображення щілини не може стати менше дифракційної межі. Тому, отримати лінії як можна тонше, марно використовувати вхідну щілину менше за нормальну.
Дифракція на вхідній щілині приладу при освітленні вхідної щілини на відстані 50–100 см від джерела світла невеликих розмірів (пунктир на рис. 4.7). З (4.15) можна отримати, що 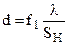 , тобто відстань від центру цієї дифракційної картини до її першого нуля
, тобто відстань від центру цієї дифракційної картини до її першого нуля 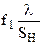 дорівнює величині діючого отвору d. В цьому випадку центральна частина головного максимуму розміщується в діючому отворі.
дорівнює величині діючого отвору d. В цьому випадку центральна частина головного максимуму розміщується в діючому отворі.
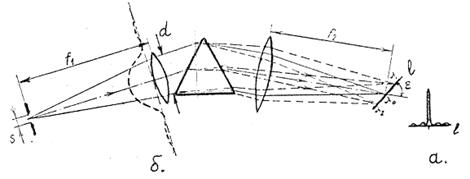
Рис. 4.7. Оптична схема призмового спектрографа: а) результат дифракції на діючому отворі приладу (впливає на роздільну здатність); б) результат дифракції на вхідній щілині приладу при когерентному освітленні щілини (впливає на величину світлового потоку, що досягає фокальної площини)
Зміна світлового потоку, що проходить в прилад, із зміною ширини щілини наведена на рис. 4.8. При s/sн<1 зі зменшенням щілини світловий потік, що проходить в прилад, і освітленість в центрі лінії швидко падають. При s/sн>1 із збільшенням щілини світловий потік (з одиниці площі щілини) слабо зростає за рахунок попадання в діючий отвір найближчих до головного дифракційних максимумів, а потім його зростання припиняється. Спектральна лінія при цьому має вигляд прямокутника, ширина якого зростає пропорційно ширині вхідної щілини.
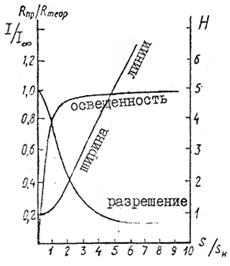
Рис. 4.8. Залежність освітленості в центрі лінії I/I¥, ширина спектральної лінії Н і роздільній здатності Rпр/Rтеор від ширини щілини sн/s
Дата добавления: 2015-08-21; просмотров: 3108;
