Метод сопоставления предельного дохода с предельными издержками
При использовании данного метода определяются и сравниваются две величины:
1) предельный доход (MR), т. е. прирост величины дохода при увеличении объема производства на одну единицу;
2) предельные издержки (МС), т. е. прирост величины валовых издержек при увеличении объема производства на одну единицу.
Любую дополнительную единицу продукции, для которой предельный доход превышает предельные издержки (MR > МС), следует производить, так как на каждой такой единице фирма получает больше дохода от ее продажи, чем она прибавляет к издержкам, производя эту единицу. Разница (прибыль) составляет величину MR - МС.
Очевидно также, что если МС > MR, т. е. предельные издержки выше предельного дохода, фирме следует избегать производства этой единицы, так как она добавляет больше к издержкам, чем к доходу на величину МС - MR; такая единица продукции не будет окупаться.
Таким образом, фирма будет максимизировать прибыль или минимизировать убытки, производя такой объем продукции, при котором предельный доход равен предельным издержкам: MR = МС. Математически это можно доказать следующим образом. Рассчитываем прибыль pr = ТR - ТС. Условие экстремума прибыли: dpr /Dq =0.
Продифференцируем функцию прибыли:
dpr d(TR) d(TС)
------- = ------- - --------= MR – МС=0
dQ Dq dQ
|
|





 Р
Р

 Р D S
Р D S
 P0 P0 АТС
P0 P0 АТС













 D. AR, MR
D. AR, MR
 |
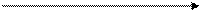
 q 0 Q q0 Q
q 0 Q q0 Q
Рис. 14. Функция переменных издержек фирмы
Отсюда следует, что для значения Q, обеспечивающего экстремум функции прибыли, MR = МС.
Дата добавления: 2015-08-14; просмотров: 903;
