Резонансные частоты и размер пучка излучения.

Резонансные частоты для общего случая сферического резонатора определяется выражением, полученным в результате решения уравнений Максвелла:

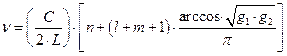(2.12)

где n, l, m – положительные целые числа, n – соответствует стоячей волне (моде), ориентированной остро вдоль оси резонатора l и m – соответствует стоячим волнам (модам), ориентированных под некоторым углом к оси резонатора. Этот угол не может иметь больших значений (иначе не будет усиления излучения) Поэтому на практике n>>l , а l и m <= 2.

Резонансные частоты могут быть представлены (рис. ) частотным спектром мод (зависимость интенсивности излучения I от частоты ν. Каждая резонансная частота, т.е. мода соответствует определенному сочетанию n,m,l – чисел.

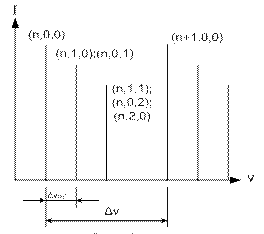
Рис.

Мода с n,0,0 – называют продольной модой.

- разность частот между двумя соседними продольными модами.

Моды, у которых m или l≠0, называют поперечными.

- разность частот между поперечными модами.

Радиусы пучка в оптическом резонаторе (при генерации излучения на продольной моде) можно определить по формулам

,

,

.

.

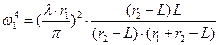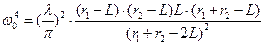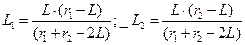При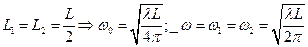

При .

.

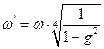На практике, как правило, стараются обеспечить условия резонанса при l=m=0, т.е. получают продольную моду.

Моды оптического резонатора и соответственно модовый состав излучения обозначают TEM _n,l,m, где TEM – transverse electric and magnetic; n,l,m – модовые числа. Так как n>>m и l (например, для СО₂ – лазера L=10² см - n=2*10⁵) обычно n – не указывают.

Пример: TEM₀₀ – продольная мода, TEM₀₁, TEM₀₂, TEM₁₁ и т. д. – различные типы поперечных мод.

Типичные картины распределения интенсивности в лазерном пучке при генерации на различных модах приведены в литературе и рис. .

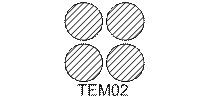
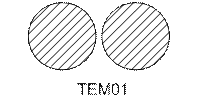
Рис.