Устойчивость динамических систем.

Линейная динамическая система называется устойчивой, если все её собственные колебания затухают во времени. Необходимыми и достаточными условиями устойчивости системы являются отрицательность вещественных частот всех корней характеристического уравнения (4). Эти корни не должны быть и чисто мнимыми. Хотя при этом собственные колебания, есть гармонические функции вида:

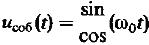(12)

Небольшие случайные изменения параметров системы могут привести к переходу её в неустойчивый режим:

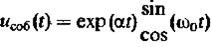(13)

Если порядок динамической системы достаточно высок, то прямая проверка устойчивости, основанная на поиске корней характеристического уравнения может оказаться весьма затруднительной, поэтому были разработаны специальные критерии устойчивости.