Построение вариационного ряда.
Виды вариационных рядов:
1. Ранжированный – это последовательность единиц совокупности, расположенных в порядке возрастания или убывания. (14,9 16,3 21,4 25,2 30,3)
2. Дискретный – это таблица, состоящая из 2-х колонок: 1-я – значение признака, 2-я – частота их появления.
| Число проданных авто | Число дней |
| Итого: |
1.Интервальный ряд – используется, когда признак принимает любые значения или признак является дискретным, но число значений велико.
| Рентабельность, % xj | Число предприятий, fj | Середина интервала, xj | Накопленная частота | |
| fj' | fj'' | |||
| 10-20 | ||||
| 20-30 | ||||
| 30-40 | ||||
| 40-50 | ||||
| 50-60 | ||||
| Итого: |
fj' – количество единиц совокупности, у которых значение признака не больше, чем верхняя граница интервала.
fj'' - количество единиц совокупности, у которых значение признака больше, чем верхняя граница интервала.
Первым этапом анализа вариационного ряда является построение гистограммы и полигона.
I-ый этап – гистограмма и полигон.
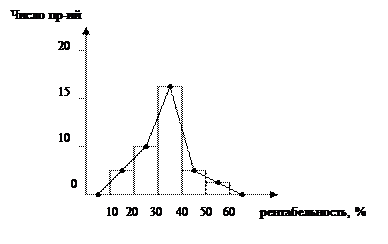 Гистограмма строится для интервального ряда.
Гистограмма строится для интервального ряда.
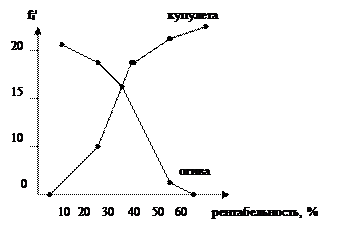
Полигон строится для интервального и дискретного ряда.
II-ой этап – расчет структурных средних
(медианы, квартилий и мозы).
Медиана
Медиана – величина анализируемого признака, которая делит совокупность на 2 части, равные по числу единиц.
В ранжированном ряду, медиана – это средняя в ряду единиц совокупности.
14,9 16,3 21,4 25,2 30,3 (Ме = 21,4)
В дискретном ряду:
| xi | fi | fi' |
 21 21
| ||
| Итого: |
Для определения медианы сначала определяются накопленные частоты.
Определяется номер единицы, которая делит совокупность на 2 части.
180/2 = 90
Медианой является значение признака, для которой накопленная частота больше или равна половине численности совокупности. Ме = 2
В интервальном ряду:
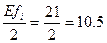
Определяем интервал, в котором находится эта единица, по накопленной частоте.
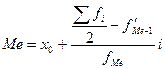 , где x0 – нижняя граница медианного интервала, f 'Me–1 – частота попадания в интервал, предшествующий медианному, fMe–1 – частота попадания в медианный интервал, i – ширина медианного интервала.
, где x0 – нижняя граница медианного интервала, f 'Me–1 – частота попадания в интервал, предшествующий медианному, fMe–1 – частота попадания в медианный интервал, i – ширина медианного интервала.
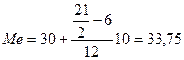
Квартили
Квартиль – это значения анализируемого признака, которые делят совокупность на 4 части, равные по … единицу.
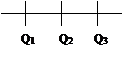 Q2 – это медиана.
Q2 – это медиана.
Для интервального ряда:
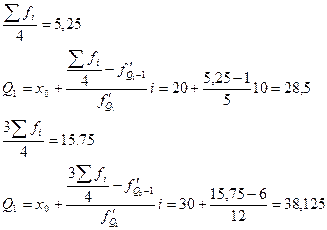
Мода
Мода – это значение признака, которое встречается чаще всего.
В ранжированном ряду моды нет.
В дискретном ряду: М0 = {1, 2}.
В интервальном ряду:
Что бы найти моду в интервальном ряду, надо выделить интервал с максимальной частотой попадания.
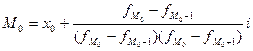 , где
, где 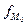 – частота попадания в модальный интервал,
– частота попадания в модальный интервал, 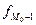 – частота попадания в предшествующий интервал,
– частота попадания в предшествующий интервал, 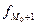 – частота попадания в следующий интервал.
– частота попадания в следующий интервал.
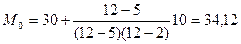
Если группировка выполнена с неравными интервалами, то моза определяется не по частоте, а по плотности распределения (частота, деленная на ширину интервала).
III-ий этап – расчет среднего анализирующего признака.
x – среднее взвешенное.
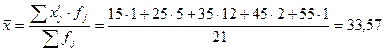
Правило:
Если распределение близко к нормальному, то медиана находится между мозой и среднем значением, причем ближе к среднему.
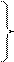
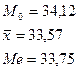 Þ нормальное распределение.
Þ нормальное распределение.
Дата добавления: 2015-08-14; просмотров: 1379;
