Многомерные группировки.
Группировочные признаки в многомерной группировке обобщаются в единый показатель, который называется мера сходства.
Чаще всего, в качестве меры сходства используются:
· Функции расстояния.
· Многомерные средние.
Многомерные средние рассчитываются по следующей формуле:
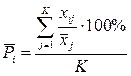 , где K – число группировочные признаков, xij – значение j-го признака у i-той единицы совокупности,
, где K – число группировочные признаков, xij – значение j-го признака у i-той единицы совокупности, 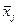 – среднее значение j-го признака.
– среднее значение j-го признака.
Пример:
| Предприятие | Рентабельность, % | Основные фонды, млн. руб. | 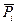
| ||
| xi1 | 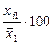
| xi2 | 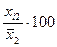
| ||
| 13,95 | 160,4 | 70,4 | 115,4 | ||
| 5,55 | 63,9 | 141,9 | 102,9 | ||
| 6,57 | 75,6 | 87,7 | 84,65 | ||
| В среднем: | 8,69 | 5,771 |
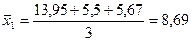 ;
;
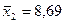
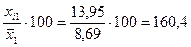
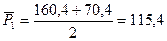
Группировка:
kприн = 2
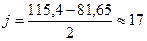
| Многомерное среднее | Количество предприятий |
| 81,65-98,65 | |
| 98,65-115,65 | |
| Итого: |
Дата добавления: 2015-08-14; просмотров: 673;
