Приведение общей ЗЛП к канонической форме
Чтобы перейти от общей формы записи ЗЛП к канонической, нужно в общем случае уметь, во-первых, сводить задачу минимизации к задаче максимизации, во-вторых, переходить от ограничений-неравенств к ограничениям равенствам, в-третьих, заменять переменные, которые не подчинены условию неотрицательности.
В том случае, когда требуется найти минимум функции  , можно перейти к нахождению максимума функции
, можно перейти к нахождению максимума функции 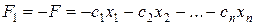 , поскольку
, поскольку 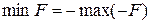 .
.
Ограничения-неравенства исходной ЗЛП можно преобразовать в ограничения-равенства добавлением к их левой части дополнительнойнеотрицательной переменной со знаком "+" в случае неравенства вида " 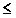 " и со знаком "-" - в случае неравенства вида "
" и со знаком "-" - в случае неравенства вида " 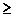 ". Таким образом, ограничение-неравенство
". Таким образом, ограничение-неравенство
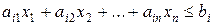
преобразуется в ограничение-равенство
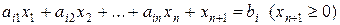 ,
,
а ограничение-неравенство
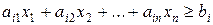
- в ограничение-равенство
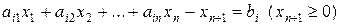 .
.
Если на переменную  не наложено условие неотрицательности, то эту переменную надо представить в виде разности двух новых неотрицательных переменных:
не наложено условие неотрицательности, то эту переменную надо представить в виде разности двух новых неотрицательных переменных: 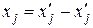 ,
, 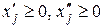 .
.
Пример 9.1. Записать в канонический форме следующую задачу линейного программирования: найти минимум функции 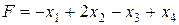 , при условиях
, при условиях
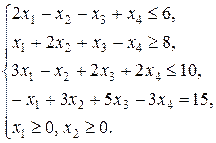
Вместо нахождения минимума функции F можно найти максимум функции 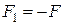 при ограничениях, получающихся из ограничений-неравенств исходной задачи с помощью дополнительных неотрицательных переменных с соответствующим знаком. В первое ограничение системы добавим переменную
при ограничениях, получающихся из ограничений-неравенств исходной задачи с помощью дополнительных неотрицательных переменных с соответствующим знаком. В первое ограничение системы добавим переменную 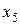 со знаком «+», во второе ограничение – переменную
со знаком «+», во второе ограничение – переменную 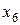 со знаком «-» и в третье ограничение системы – переменную
со знаком «-» и в третье ограничение системы – переменную 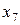 со знаком «+». Так как на переменные
со знаком «+». Так как на переменные 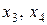 не наложено условие неотрицательности, то необходимо произвести следующую замену переменных:
не наложено условие неотрицательности, то необходимо произвести следующую замену переменных:
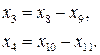
Следовательно, исходная задача может быть записана в канонической форме так: найти максимум функции 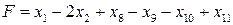 при условиях:
при условиях:
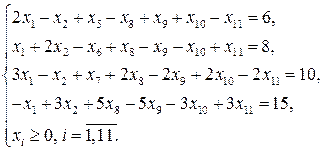
Множество планов ЗЛП и его свойства
Определение 9.2. Множество векторов X, удовлетворяющих ограничениям задачи составляет множество допустимых планов данной задачи M= 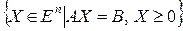 .
.
Тогда каноническую ЗЛП в матричной форме можно переписать следующим образом: 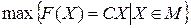 .
.
Решить данную ЗЛП, значит найти оптимальный план задачи, т.е. такой план задачи, значение линейной формы в котором максимально: 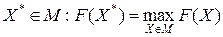 .
.
Теорема 9.1. Множество 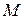 планов ЗЛП является выпуклым множеством.
планов ЗЛП является выпуклым множеством.
Д о к а з а т е л ь с т в о. Множество называется выпуклым, если любые две его точки входят в него вместе с отрезком их соединяющим. Таким образом, чтобы доказать выпуклость М, надо доказать, то что для любых 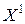 и
и 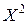 принадлежащих множеству М справедливо
принадлежащих множеству М справедливо 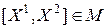 .
.
Пусть 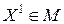 и
и 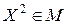 . Это значит, что координаты этих точек удовлетворяют условиям задачи, т.е.
. Это значит, что координаты этих точек удовлетворяют условиям задачи, т.е.  ,
, 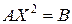 .
.
Выберем некоторый параметр 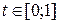 и умножим равенство
и умножим равенство  на
на 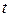 , а
, а 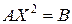 - на
- на 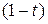 . Складывая результаты получим:
. Складывая результаты получим:
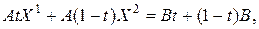
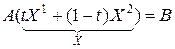
т.е. точка  , являющаяся произвольной точкой отрезка
, являющаяся произвольной точкой отрезка 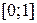 , удовлетворяет условиям задачи, а значит принадлежит множеству
, удовлетворяет условиям задачи, а значит принадлежит множеству 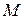 . Значит и весь отрезок
. Значит и весь отрезок 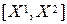 также принадлежит множеству
также принадлежит множеству 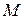 . Следовательно, множество М выпукло.
. Следовательно, множество М выпукло.
Теорема 9.2.Множество 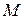 планов ЗЛП является замкнутым множеством.
планов ЗЛП является замкнутым множеством.
Д о к а з а т е л ь с т в о. Замкнутым называется множество, содержащее все свои граничные точки. Точка называется граничной точкой множества, если в любой окрестности этой точки есть как точки множества, так и точки ему не принадлежащие. Если 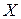 - граничная точка
- граничная точка 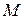 , то существует последовательность
, то существует последовательность 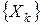 принадлежащая
принадлежащая 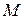 такая, что
такая, что
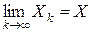 ,
,
а сама точка 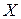 называется предельной. Поэтому все граничные точки являются предельными точками множества М. Все внутренние точки тем более
называется предельной. Поэтому все граничные точки являются предельными точками множества М. Все внутренние точки тем более
являются предельными.
Пусть Х- произвольная предельная точка множества М и пусть последовательность 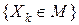 , такая что
, такая что 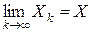 . Так как все
. Так как все 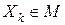 , то для любого
, то для любого 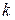 выполняется условие
выполняется условие 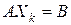 . Тогда
. Тогда
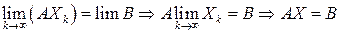
То есть, все предельные точки 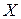 принадлежат множеству
принадлежат множеству 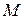 . Следовательно, множество М замкнуто.
. Следовательно, множество М замкнуто.
Теорема 9.3. Множество 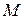 планов ЗЛП является многогранным множеством.
планов ЗЛП является многогранным множеством.
Д о к а з а т е л ь с т в о. Гиперплоскостью в 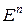 называется множество
называется множество 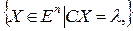 . Гиперплоскость
. Гиперплоскость 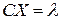 делит все пространство на два полупространства: нижнее
делит все пространство на два полупространства: нижнее 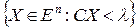 и верхнее
и верхнее 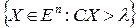 . Множество, являющееся пересечением конечного числа гиперплоскостей и подпространств называется многогранным множеством.
. Множество, являющееся пересечением конечного числа гиперплоскостей и подпространств называется многогранным множеством.
Следовательно, множество планов ЗЛП, являющееся множеством точек 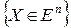 , удовлетворяющих системе конечного числа линейных уравнений и неравенств, есть многогранное множество
, удовлетворяющих системе конечного числа линейных уравнений и неравенств, есть многогранное множество
Определение 9.3. Точка 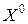 называется угловой точкой множества M, если никакой отрезок, содержащий
называется угловой точкой множества M, если никакой отрезок, содержащий 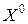 в качестве своей внутренней точки, не содержится целиком во множестве M.
в качестве своей внутренней точки, не содержится целиком во множестве M.
Теорема 9.4. Чтобы точка 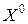 множества M планов ЗЛП, имеющая хотя бы одну положительную координату, являлась угловой точкой, необходимо и достаточно, чтобы вектора условий, соответствующие положительным координатам были линейно независимы.
множества M планов ЗЛП, имеющая хотя бы одну положительную координату, являлась угловой точкой, необходимо и достаточно, чтобы вектора условий, соответствующие положительным координатам были линейно независимы.
Д о к а з а т е л ь с т в о. Необходимость. Пусть 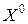 - угловая точка множества планов ЗЛП такая что координаты
- угловая точка множества планов ЗЛП такая что координаты 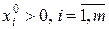 , а остальные координаты
, а остальные координаты 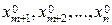 равны нулю.
равны нулю.
Предположим противное: система векторов 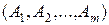 - линейно зависима. Тогда существуют числа
- линейно зависима. Тогда существуют числа 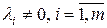 не все равные нулю, такие что
не все равные нулю, такие что
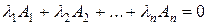 (9.8)
(9.8)
С другой стороны, так как 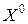 принадлежит
принадлежит 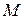 , то должно выполняться равенство
, то должно выполняться равенство
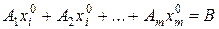 (9.9)
(9.9)
Умножим обе части равенства (9.8) на произвольное положительноечисло 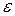 малое настолько, что все числа
малое настолько, что все числа 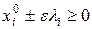 . Прибавляя и вычитая результат из соотношения (9.9), получим
. Прибавляя и вычитая результат из соотношения (9.9), получим
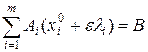 , т.е.
, т.е. 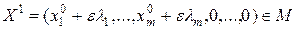
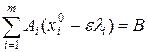 , т.е.
, т.е. 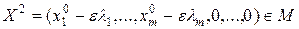
Очевидно, 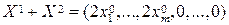 , то есть
, то есть 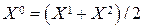
Это означает, что 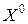 является внутренней точкой отрезка с концами
является внутренней точкой отрезка с концами 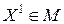 и
и 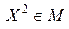 . Получили противоречие, ибо условие, что
. Получили противоречие, ибо условие, что 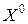 является угловой точкой множества
является угловой точкой множества 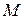 , исключает существование такого отрезка. Итак, допущение о линейной зависимости векторов
, исключает существование такого отрезка. Итак, допущение о линейной зависимости векторов 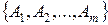 не верно, следовательно, они линейно независимы.
не верно, следовательно, они линейно независимы.
Достаточность. Пусть вектора 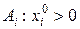 - линейно независимы и наряду с этим
- линейно независимы и наряду с этим 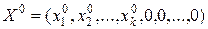 - не является угловой точкой. Тогда, существует отрезок с концами в точках
- не является угловой точкой. Тогда, существует отрезок с концами в точках 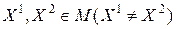 , содержащий
, содержащий 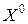 в качестве внутренней точки, т.е.
в качестве внутренней точки, т.е.
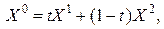
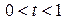 .
.
Из этого равенства, с учетом условий 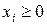 , следует, что если некоторые числа
, следует, что если некоторые числа 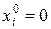 , то и числа
, то и числа 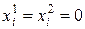 .
.
Далее в силу принадлежности точек 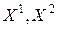 множеству
множеству 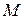 имеем
имеем
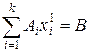 ,
, 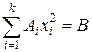 .
.
Вычитая из одного равенства другое, получим
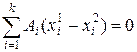 .
.
Точки 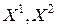 различны, поэтому хотя бы одна из разностей, стоящих коэффициентами при
различны, поэтому хотя бы одна из разностей, стоящих коэффициентами при 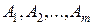 , отлична от нуля. Отсюда следует, что столбцы
, отлична от нуля. Отсюда следует, что столбцы 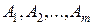 линейно зависимы. Полученное противоречие доказывает, что точка
линейно зависимы. Полученное противоречие доказывает, что точка 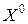 является угловой точкой множества планов
является угловой точкой множества планов 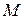 .
.
Следствие 1. Любая угловая точка 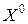 множества планов ЗЛП может иметь не более r положительных компонент, где r - ранг матрицы условий (
множества планов ЗЛП может иметь не более r положительных компонент, где r - ранг матрицы условий ( 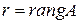 ).
).
Следствие 2. Для любой угловой точки множества планов ЗЛП количество линейно независимых векторов, соответствующих положительным координатам, не может быть больше ранга матрицы условий.
Пользуясь данными утверждениями об угловых точках можно:
· проверить, является ли некоторая заданная точка угловой или нет;
· построить угловую точку данного множества.
Для ответа на первый вопрос нужно проверить являются ли вектора условий, соответствующие положительным координатам данной точки, линейно независимыми.
Построить угловую точку заданного множества планов можно по следующему алгоритму:
1. Вычислить ранг 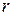 матрицы условий
матрицы условий 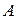 . При этом, в матрице
. При этом, в матрице 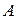 найдется система
найдется система 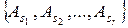 линейно независимых векторов.
линейно независимых векторов.
2. Всем координатам, номера которых не совпадают с номерами выделенных векторов условий присвоить нулевое значение, т.е. 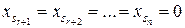 .
.
3. Тогда оставшиеся 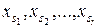 могут быть найдены в результате решения системы, полученной из исходной, приравниванием нулю координат
могут быть найдены в результате решения системы, полученной из исходной, приравниванием нулю координат 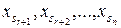 . Определитель полученной системы отличен от нуля по построению, а значит, система имеет единственное решение. При этом если все найденные в результате решения числа неотрицательные (
. Определитель полученной системы отличен от нуля по построению, а значит, система имеет единственное решение. При этом если все найденные в результате решения числа неотрицательные ( 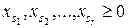 ), то найденная точка
), то найденная точка 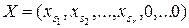 является угловой. Если же хотя бы одна координата оказалась отрицательной, то точка
является угловой. Если же хотя бы одна координата оказалась отрицательной, то точка 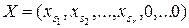 не является угловой и не является даже планом задачи. Тогда нужно выбрать другую систему линейно независимых векторов и перейти к пункту 2.
не является угловой и не является даже планом задачи. Тогда нужно выбрать другую систему линейно независимых векторов и перейти к пункту 2.
Число столбцов в матрице 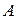 конечно, а значит и число всевозможных линейно независимых систем
конечно, а значит и число всевозможных линейно независимых систем  тоже конечно, т.е. число опорных планов множества планов ЗЛП конечно.
тоже конечно, т.е. число опорных планов множества планов ЗЛП конечно.
Определение 9.4. План ЗЛП, соответствующий угловой точке множества планов называется опорным планом.
Определение 9.5. Базисом опорного плана называется любая система из r (где 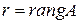 ) линейно независимых столбцов
) линейно независимых столбцов 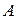 , включающая все столбцы, соответствующие положительным координатам
, включающая все столбцы, соответствующие положительным координатам 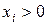 . Столбцы, входящие в базис, называются базисными. Составляющие опорного плана, соответствующие базисным столбцам называются базисными компонентами.
. Столбцы, входящие в базис, называются базисными. Составляющие опорного плана, соответствующие базисным столбцам называются базисными компонентами.
Определение 9.6. Опорный план называется невырожденным, если число положительных компонент равно рангу матрицы условий. Опорный план называется вырожденным, если число положительных координат меньше ранга матрицы условий.
Невырожденный опорный план имеет единственный базис, а вырожденный опорный план может иметь несколько базисов, т.к. столбцы, соответствующие положительным компонентам, а их меньше r, могут быть дополнены до системы из r линейно независимых столбцов присоединением различных столбцов. Все небазисные компоненты любого опорного плана (вырожденного или невырожденного) равны нулю. Все базисные компоненты невырожденного опорного плана строго больше нуля.
Пример 9.2. Пусть множество допустимых планов M задано системой уравнений:
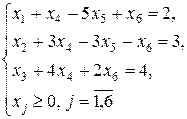
Найдем угловую точку данного множества.
Выпишем матрицу условий 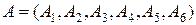 :
:
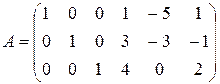
Нетрудно заметить, что столбцы 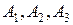 - составляют минор 3-го порядка отличный от нуля, следовательно, ранг матрицы A равен 3. Тогда координаты
- составляют минор 3-го порядка отличный от нуля, следовательно, ранг матрицы A равен 3. Тогда координаты 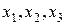 являются базисными компонентами, а
являются базисными компонентами, а 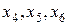 - небазисными. Приравнивая в исходной системе небазисные переменные нулю, получим систему:
- небазисными. Приравнивая в исходной системе небазисные переменные нулю, получим систему:
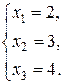
Таким образом, мы нашли угловую точку 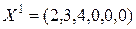 множества M т.к. все ее координаты неотрицательны, а вектора условий, соответствующие положительным координатам линейно независимы. Базис полученного опорного плана
множества M т.к. все ее координаты неотрицательны, а вектора условий, соответствующие положительным координатам линейно независимы. Базис полученного опорного плана 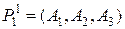 единственный, т.к. план является невырожденным.
единственный, т.к. план является невырожденным.
Проверим, является ли вектор 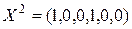 угловой точкой множества M.
угловой точкой множества M.
Подставим координаты точки в исходную систему ограничений:
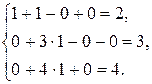
Таким образом, координаты 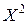 удовлетворяют ограничениям задачи, следовательно,
удовлетворяют ограничениям задачи, следовательно, 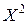 является планом задачи.
является планом задачи.
Легко проверить, что ранг матрицы 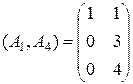 равен 2, следовательно, вектора
равен 2, следовательно, вектора 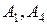 - линейно независимы, а значит, план
- линейно независимы, а значит, план 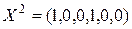 является опорным. Т.к. ранг матрицы A равен 3, а количество неотрицательных компонент данного опорного плана - 2, то план является вырожденным. Данный опорный план может иметь несколько базисов, которые можно получить присоединением различных векторов.
является опорным. Т.к. ранг матрицы A равен 3, а количество неотрицательных компонент данного опорного плана - 2, то план является вырожденным. Данный опорный план может иметь несколько базисов, которые можно получить присоединением различных векторов.
Рассмотрим систему из трех векторов 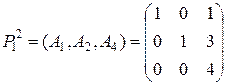
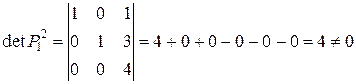
Система векторов 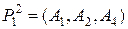 - линейно независима, т.к.
- линейно независима, т.к. 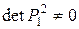 , следовательно
, следовательно 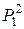 - базис опорного плана
- базис опорного плана 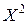 . Аналогично можно проверить, что
. Аналогично можно проверить, что 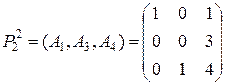 также является базисом опорного плана
также является базисом опорного плана 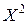 .
.
Теоремы о представлении множества планов ЗЛП
Теорема 9.5 (теорема о представлении множества планов ЗЛП). Пусть множество планов ЗЛП 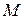 - выпуклое замкнутое ограниченное множество,
- выпуклое замкнутое ограниченное множество, 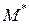 - совокупность всех угловых точек
- совокупность всех угловых точек 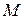 . В таком случае множество
. В таком случае множество 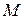 является выпуклой оболочкой множества
является выпуклой оболочкой множества 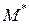 , т.е.
, т.е.
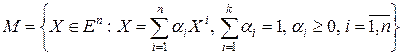
Эта теорема позволяет представить все многообразие точек многогранника через конечное число его угловых точек. Коэффициенты  определяются однозначно только в том случае, если множество
определяются однозначно только в том случае, если множество  имеет ровно
имеет ровно  угловых точек. Такой многогранник называется симплексом.
угловых точек. Такой многогранник называется симплексом.
Пример 9.3. Симплекс в пространстве 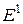 . Убедимся, что
. Убедимся, что 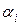 определяются однозначно для любого
определяются однозначно для любого 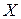 из
из 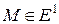 (рис. 9.1).
(рис. 9.1).

Рис 9.1. Множество 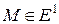 .
.
Любую внутреннюю точку отрезка 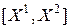 можно представить как
можно представить как  ,
, 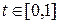 . Введем следующие обозначения
. Введем следующие обозначения
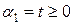 ,
, 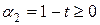
Таким образом, существуют 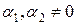 :
: 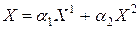 ,
, 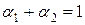 ,
, 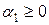 ,
, 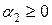 .
.
Пример 9.4. Симплекс в пространстве 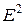 . Убедимся, что
. Убедимся, что 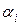 определяются однозначно для любого
определяются однозначно для любого 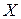 из
из 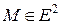 (рис 9.4).
(рис 9.4).

Рис 9.4. Множество 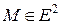 .
.
Для симплекса в 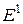 выше показана однозначность представления. Значит
выше показана однозначность представления. Значит
· для 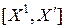 имеем
имеем 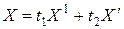 ,
, 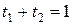 ,
,  ,
, 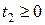 ;
;
· для 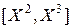 имеем
имеем 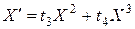 ,
, 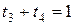 ,
, 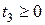 ,
, 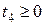 .
.
Объединяя, получим
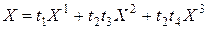 .
.
Если обозначить 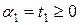 ,
, 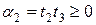 ,
, 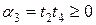 , то
, то
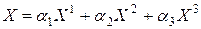 ,
,
причем
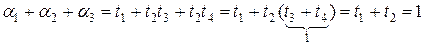 ,
,
т.е. однозначно нашли коэффициенты 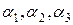 такие, что
такие, что
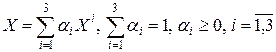 ,
,
для любого 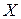 из
из 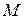 .
.
Теорема 9.6 (теорема о представлении неограниченного многогранного множества планов ЗЛП). Пусть множество планов ЗЛП 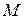 - выпуклое неограниченное замкнутое множество. Точки
- выпуклое неограниченное замкнутое множество. Точки 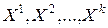 - все угловые точки множества
- все угловые точки множества 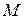 ,
, 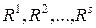 - направляющие вектора его неограниченных ребер. Тогда множество
- направляющие вектора его неограниченных ребер. Тогда множество 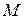 совпадает с совокупностью точек
совпадает с совокупностью точек 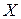 вида
вида
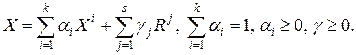
Дата добавления: 2015-08-14; просмотров: 2524;
