Главные площадки и главные напряжения

ЛЕКЦИЯ №6

Нарисуем треугольную призму и действующими силами из предыдущей лекции.

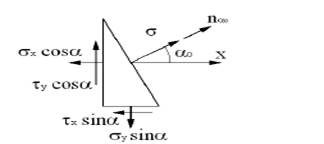
Пусть наклонная площадка треугольной призмы является главной площадкой. угол наклона главной площадки. Так как площадка главная, то на ней нет касательных напряжений. Нормальные напряжения на ней обозначим как .

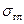Обозначим 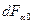площадь наклонной площадки. 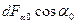- площадь вертикальной площадки.

Спроектируем все силы на оси x и y

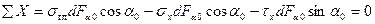
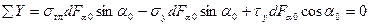
Сократим , заменим 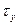на 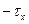, поделим на 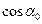и исключим из уравнения tgα₀. В результате получим квадратное уравнение относительно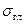

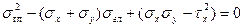
Решая квадратное уравнение, получим формулу для главных напряжений при плоском напряженном состоянии

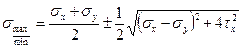(10)

Всегда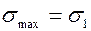

Так как на главной площадке , то выражение (7)=0 если α=α₀

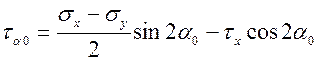:cos2α₀

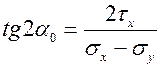(11) формула для определения угла наклона главных площадок

Позволяет определить углы наклона 2-х взаимно-перпендикулярных главных площадок.

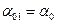
Но в каком направлении не знаем.

Для определения направления главных напряжений используем знак двойной производной от σ_α по α. .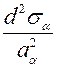

Исследовать не будем, а приведем результаты

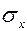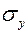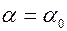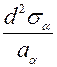При > и → < 0 , то функция 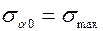принимает максимальное значение.

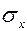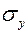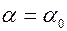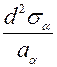При < и → > 0 , то функция 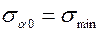принимает минимальное значение.

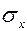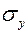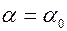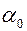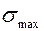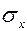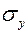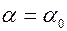Вывод: если > и , то под углом действует и наоборот если < и то под углом 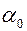действует .

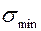Проверка. Главное напряжение 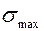всегда пересекает те четверти осей координат, где стрелки касательных напряжений сходятся.

Покажем направления главных площадок на элементе используемом для вывода.

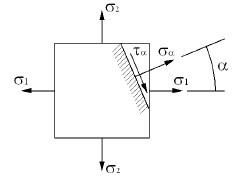
Пусть >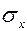

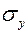
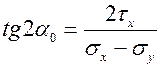>0

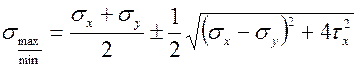
Может быть неправильно построили? Используем проверку дальше (см. выше).