Свободные затухающие электромагнитные колебания.
Т.к. всякий проводник обладает сопротивлением, в процессе прохождения тока в колебательном контуре выделяется джоулево тепло, т.е. теряется энергия, поэтому свободные электромагнитные колебания в реальном контуре (рис. 5) всегда затухающие. Для такого контура
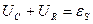 , где
, где 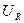 - падение напряжения на активном сопротивлении контура.
- падение напряжения на активном сопротивлении контура.
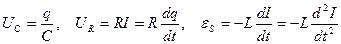 ,
,
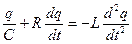 или
или 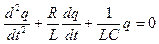 .
.
Обозначим 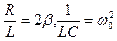 .
.
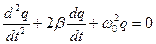 - дифференциальное уравнение свободных затухающих электромагнитных колебаний.
- дифференциальное уравнение свободных затухающих электромагнитных колебаний.
Решением этого уравнения является выражение 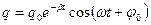 .
.
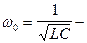 циклическая частота собственных незатухающих колебаний;
циклическая частота собственных незатухающих колебаний;
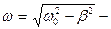 циклическая частота собственных затухающих колебаний;
циклическая частота собственных затухающих колебаний;
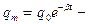 закон убывания амплитуды (рис.6), где
закон убывания амплитуды (рис.6), где 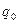 - амплитуда при t=0.
- амплитуда при t=0.
 |
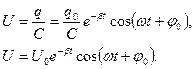
Выясним физический смысл b. Введем понятие времени реакции t - времени, за которое амплитуда уменьшается в е раз.
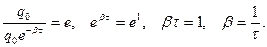
Таким образом, b есть величина, обратная t.
Логарифмический декремент затухания - натуральный логарифм отношения 2-х амплитуд, отличающихся по времени на период.
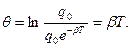
За время t система совершит 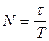 колебаний.
колебаний.
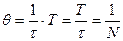 ,
,
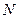 - число колебаний, за которые амплитуда уменьшается в е раз.
- число колебаний, за которые амплитуда уменьшается в е раз.
Добротность характеризует способность колебательного контура к затуханию колебаний:
Q 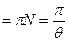 .
.
Добротность пропорциональна числу колебаний, за которые амплитуда уменьшается в е раз.
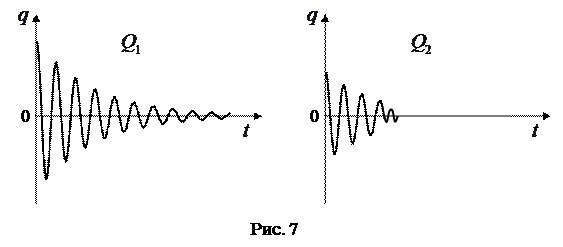
Если Q велико, колебания затухают медленно (рис.7, 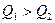 ).
).
 |
Дата добавления: 2015-08-14; просмотров: 1556;
