Свободные незатухающие колебания в колебательном контуре.
Среди электрических явлений особое место занимают электромагнитные колебания, при которых электрические величины (заряды, токи, электрические и магнитные поля) изменяются периодически. Для возбуждения и поддерживания электромагнитных колебаний требуются определенные системы, простейшей из которых является колебательный контур.
Колебательный контур - это цепь, состоящая из последовательно соединенных катушки индуктивностью 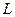 и конденсатора емкостью
и конденсатора емкостью 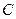 .
.
Рассмотрим процесс возникновения электромагнитных колебаний в идеализированном колебательном контуре, в котором можно пренебречь сопротивлением соединительных проводов. Для возбуждения в контуре колебаний конденсатор предварительно заряжают, сообщая его обкладкам заряд q0 от внешнего источника (рис.1).
 |
В заряженном колебательном контуре устанавливаются свободные колебания, называемые электромагнитными. При этом колеблются значения всех электрических и магнитных величин.
В контуре возникают электромагнитные колебания, при которых происходит превращение энергии электрического поля в энергию магнитного поля и наоборот. Рисунок 2 представляет собой график зависимости заряда конденсатора 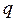 от времени
от времени 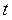 ,
, 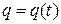 , на котором значениям заряда в моменты времени
, на котором значениям заряда в моменты времени 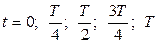 сопоставлены соответствующие состояния колебательного контура (а; б; в; г; д).
сопоставлены соответствующие состояния колебательного контура (а; б; в; г; д).
Электромагнитные колебания во многом подобны механическим колебаниям, т.е. подобны описывающие их уравнения и их решения.
Запишем для контура 2-е правило Кирхгофа для произвольного момента времени: сумма падений напряжений равна сумме действующих в контуре эдс. В контуре действует только одна эдс - эдс самоиндукции 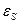 , а падение напряжения происходит на конденсаторе, поэтому
, а падение напряжения происходит на конденсаторе, поэтому 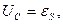
где 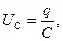
 - мгновенное значение заряда на обкладках конденсатора.
- мгновенное значение заряда на обкладках конденсатора.
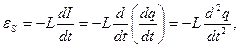
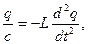
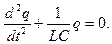
Обозначим 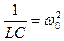 ;
;
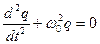 - дифференциальное уравнение свободных электромагнитных колебаний.
- дифференциальное уравнение свободных электромагнитных колебаний.
Решением этого уравнения является выражение 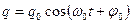 .
.
Таким образом, в идеальном колебательном контуре (рис.3) колебания заряда происходят по гармоническому закону (рис.4).
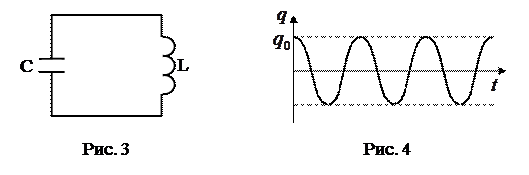

 ,
,
т.е. колебания тока опережают колебания заряда по фазе на 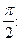 когда ток достигает максимального значения, заряд и напряжение обращаются в нуль (и наоборот).
когда ток достигает максимального значения, заряд и напряжение обращаются в нуль (и наоборот).
Т.к. 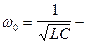 собственная циклическая частота контура,
собственная циклическая частота контура,
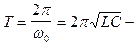 формула Томсона.
формула Томсона.
Превращение энергии в колебательном контуре:
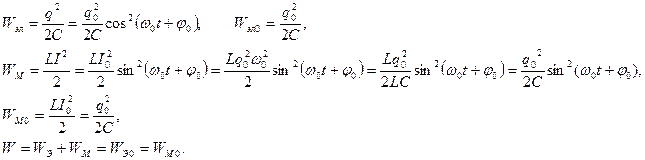
Дата добавления: 2015-08-14; просмотров: 5101;
