Математических моделей.
С помощью преобразования Лапласа дифференциальные уравнения могут быть преобразованы в алгебраические, которые гораздо легче анализировать и решать. Преобразование некоторой функции времени по Лапласу заключается во взятии интеграла от этой функции следующего вида:
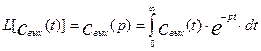
 (3.1.12)
(3.1.12)
где L –символ преобразования Лапласа; 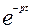 - ядро преобразования;
- ядро преобразования; 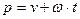 – оператор Лапласа (комплексное число); v, w - действительная и мнимая части комплексного числа. Преобразуемая функция
– оператор Лапласа (комплексное число); v, w - действительная и мнимая части комплексного числа. Преобразуемая функция 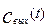 называется в этом случае оригиналом, а преобразованная
называется в этом случае оригиналом, а преобразованная 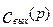 - изображением. Рассмотрим несколько примеров применения преобразования Лапласа к некоторым функциям.
- изображением. Рассмотрим несколько примеров применения преобразования Лапласа к некоторым функциям.
Пример 1. Требуется преобразовать по Лапласу функцию вида - 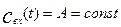 Тогда изображение будет иметь вид:
Тогда изображение будет иметь вид:
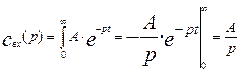 (3.1.13)
(3.1.13)
Пример 2.Требуется преобразовать по Лапласу функцию вида 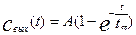 при
при 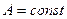 . Подставив данную функцию в равнение(3.1.12), получим:
. Подставив данную функцию в равнение(3.1.12), получим:
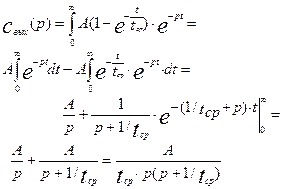 (3.1.14)
(3.1.14)
Для перехода от изображения 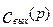 к оригиналу
к оригиналу 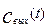 используется обратное преобразование Лапласа. Символ обратного преобразования Лапласа L-1. Провести обратное преобразование Лапласа над функцией
используется обратное преобразование Лапласа. Символ обратного преобразования Лапласа L-1. Провести обратное преобразование Лапласа над функцией 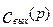 – это значит взять интеграл вида:
– это значит взять интеграл вида: 
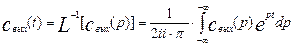 (3.1.15)
(3.1.15)
Для большинства функций значения прямого и обратного преобразования Лапласа известны и приведены в справочных таблицах.
Рассмотрим некоторые свойства преобразования Лапласа:
1. Каждый член уравнения преобразуется отдельно (свойство линейности преобразования)
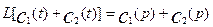 (3.1.16)
(3.1.16)
2. Дифференцированию оригинала в области действительного переменного t соответствует умножению на р в степени, равной порядку производной (при нулевых начальных условиях)
 (3.1.17)
(3.1.17)
2. Интегрированию оригинала соответствует деление изображения на переменную р в степени, равной порядку интегрирования (при нулевых начальных условиях).
3. Запаздыванию в области действительного переменного на величину 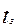 соответствует умножение изображение на величину
соответствует умножение изображение на величину 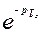 :
:
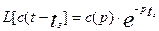 (3.1.18)
(3.1.18)
Преобразование Лапласа тесно связано с понятием передаточной функции W(p). Передаточной функцией объекта называют отношение преобразованной по Лапласу выходной характеристики объекта к преобразованной по Лапласу входной характеристике при нулевых начальных условиях:
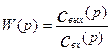 (3.1.19)
(3.1.19)
Из выражения (3.1.19) легко найти связь между выходной и входной характеристиками объекта через передаточную функцию:
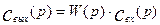 (3.1.20)
(3.1.20)
Для нахождения оригинала функции по ее изображению необходимо выполнить обратное преобразование Лапласа:
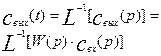 (3.1.21)
(3.1.21)
Если входная величина есть 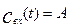 , то, учитывая выражение (3.1.21) и формулу (3.1.13), получим:
, то, учитывая выражение (3.1.21) и формулу (3.1.13), получим:
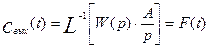 (3.1.22)
(3.1.22)
Изменение во времени выходной характеристики объекта при нанесении на вход ступенчатого возмущения 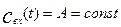 , если до нанесения возмущения объект находился в состоянии равновесия, называется кривой разгона, или F – кривой. Следовательно, уравнение (3.1.22) выражает связь кривой разгона с передаточной функцией объекта. Если в качестве входного возмущения используется импульсное возмущение типа функции Дирака d(t), то, учитывая выражение (3.1.21) а также значение преобразованной по Лапласу функции Дирака
, если до нанесения возмущения объект находился в состоянии равновесия, называется кривой разгона, или F – кривой. Следовательно, уравнение (3.1.22) выражает связь кривой разгона с передаточной функцией объекта. Если в качестве входного возмущения используется импульсное возмущение типа функции Дирака d(t), то, учитывая выражение (3.1.21) а также значение преобразованной по Лапласу функции Дирака 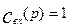 , получим для выходной характеристики следующее выражение:
, получим для выходной характеристики следующее выражение:
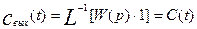 (3.1.23)
(3.1.23)
Изменение выходного параметра объекта во времени при нанесении на вход импульсного возмущения, называется импульсной характеристикой объекта, или С - кривой. Найдем передаточную функцию, а также кривую разгона и импульсную характеристику для объекта, описываемого моделью идеального перемешивания.
Математическая модель идеального перемешивания, в соответствии с ранее полученным уравнением имеет вид:
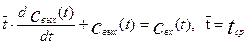
Преобразуем это уравнение по Лапласу:
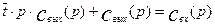 (3.1.24)
(3.1.24)
Из уравнения (3.1.24) найдем передаточную функцию:
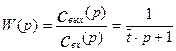 (3.1.25)
(3.1.25)
Учитывая выражение (3.22), найдем выражение для F-кривой:
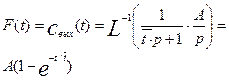 (3.1.26)
(3.1.26)
Уравнение (3.1.26) полностью соответствует уравнению (3.1.10) полученному прямым интегрированием уравнения математической модели при ступенчатой функции изменения входной концентрации. График изменения этой функции во времени приведен на рис.3.1.2.
Аналогично найдем импульсную характеристику объекта полного перемешивания:
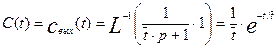 (3.1.27)
(3.1.27)
При 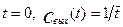 t=0, при
t=0, при 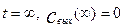
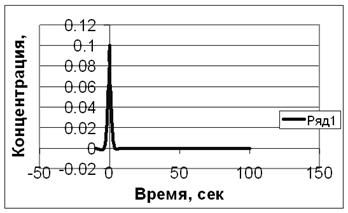
График изменения С – кривой показан на рис.3.1.3.
 |
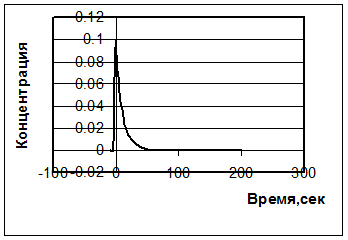 |
Рис.3.1.3а. Зависимость входной концентрации от времени
Рис3.1.3.б. Зависимость выходной концентрации от времени.
Дата добавления: 2015-08-14; просмотров: 970;
