Санкт-Петербург. Санкт-Петербургский государственный горный институт
Санкт-Петербургский государственный горный институт
(технический университет)
Кафедра автоматизации технологических процессов
И производств
Моделирование систем.
Часть 1
Учебное пособие
Специальностей 150103
«Автоматизация технологических процессов»
«Оборудование процессов переработки нефти
и газа"
Составители: Шариков Ю.В., Белоглазов И.Н.
Санкт-Петербург
СПбГГИ(ТУ)
Учебное пособие по моделированию систем
Составители: Шариков Ю.В., Белоглазов
1. Введение. Основные понятия систем.. 4
1.1.Очень большая система. 7
1.2.Общая структура сложных объектов систем.. 15
и основные этапы моделирования. 15
1.2.1.Формализованное описание. 15
1.2.2.Математическое описание. 18
1.2.3.Моделирующий алгоритм. 19
2. Общие принципы и этапы построения математических моделей систем. 21
2.2. Обобщенная структурная модель. 24
металлургического процесса. 24
3. Модели структуры потоков для технологических. 28
объектов. 28
3.1 Модель идеального перемешивания. 28
Раздел 3.2 .Модель идеального вытеснения. 39
3.3. Ячеечная модель аппарата. 43
Раздел 3.4. Диффузионная модель. 45
Стационарный метод определения критерия Пекле. 53
3.5.Комбинированные модели. 57
3.5.1.Модель с застойной зоной. 58
3.5.2.Модель с байпасным потоком. 61
3.5.3.Последовательное соединение ячеек идеального вытеснения и идеального смешения. 63
3.5.4.Гидродинамические модели многофазных. 65
потоков. 65
3.6.Методы определения параметров моделей. 67
структуры потоков. 67
3.6.1. Характеристики кривых отклика аппаратов на возмущения с помощью моментов. 67
3.6.2. Связь передаточных функций с моментами кривых. 69
3.6.3.Ячеечная модель. 72
4. Кинетические модели для описания химических превращений. 85
4.1.Основные закономерности химической кинетики. 85
4.2. Методы определения параметров кинетических моделей. 89
4.2.1.Определение констант скорости параллельных реакций: 100
4.3.Определение кинетических констант сложных реакций методами нелинейного программирования. 102
4.4. Кинетика гетерогенных процессов. 110
4.4.1 Типы гетерогенных процессов. 110
4.4.2.Основные стадии гетерогенных процессов. 110
4.4.3.Определение области протекания. 113
гетерогенного процесса. 113
Влияние формы межфазной поверхности раздела фаз на скорость гетерогенных процессов. 115
Раздел 5. Синтез моделей технологических объектов на базе их гидродинамических моделей и уравнений химической кинетики. 120
5.1. Модель идеального смешения. 120
5.2.Модель идеального вытеснения: 123
5.3. Диффузионная модель. 124
Литература. 126
1. Введение. Основные понятия систем
Сложные природные явления и технические системы исследуются на основе системного подхода. Существует множество определений систем. Мы приведем здесь одно из определений, наиболее подходящее для анализа сложных технических систем как объектов управления, а также рассмотрим некоторые определения их свойств.
Система- это организованное множество элементов (произвольной природы), обладающее относительной целостностью и полифункциональностью, иерархической организацией, включающей в себя составы и структуры. При этом эти структуры включают в себя различные характеристики, Это могут быть логические структуры, пространственно-временные, стохастические и т.д. Система характеризуется также динамикой, охватывающей функционирование и развитие с учетом характера взаимодействия с другими системами.
Важнейшими характеристиками системы является функция, цель и структура. Под функциейсистемы понимают такие действия системы, которые выражаются в изменении ее возможных состояний. Во время функционирования совершается переход системы из одного возможного состояния в другие. Множество всех возможных состояний системы определяется числом ее элементов, их свойствами и разнообразием связей между ними. Допустим, что мы выделили систему из окружающей среды и определили, что в ней находится n элементов. Между n элементами существует n(n-1) связей. Если для примера взять систему из 7 элементов, то в ней существует 42 связи. Если определить состояние системы в виде цепи, в которой каждая из этих связей реализована или отсутствует, то число различных состояний, в которых может находиться система составит 242. Это фантастически большое число, превышающее 4×1012.
Это обстоятельство является основной причиной, обуславливающей сложность и необычность задачи строгого и полного исследования систем.
Функция системы характеризует ее как единое целое, как результат взаимодействия ее элементов между собой и с внешними системами.
Цельюсистемы называется определенное (заданное извне или устанавливаемое самой системой) наиболее предпочитаемое конечное состояние ( например некоторая функция ее выходных характеристик), т.е. некоторое подмножество значений функций системы.
Структура системы определяется расположением и взаимосвязями между составляющими элементами системы, которые образованы для выполнения системой своей функции. Величина системы характеризуется числом ее элементов и количеством связей, а сложность – многообразием элементов, неоднородностью их свойств и разным качеством связей.
Функционирование системы характеризуется обычно некоторым критерием качества функционирования системы, который наиболее часто выражается следующим образом:
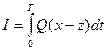 (1.1)
(1.1)
Где x –вектор, характеризующий состояние системы,
z – вектор заданного состояния системы,
Q – вектор-функция, определяемая особенностямии целью функционирования системы
Формирование критерия качества функционирования динамических систем напрямую зависит от свойства системы, называемого наблюдаемостью системы.
Наблюдаемость системы - это возможность отслеживать в процессе движения основные переменные состояния, характеризующие процессе, в количестве, достаточном для вычисления критерия качества функционирования системы.
Система является детерминированной, если при заданном начальном состоянии системы х(0)=с и заданном векторе управляющих функций.u(t) состояние системы в любой момент времени будет определено однозначно. Свойство системы следовать по предписанному движению под воздействием выбранного управления, называется управляемостью системы
Система, которая может двигаться при наложении управления из заданного начального состояния и одновременном действии возмущений, называется недетерминированной системой. Такая система может приходить в предписанное состояние только с некоторой долей вероятности
Большинство сложных технических систем, к которым относятся системы получения и обработки металлов в металлургии, процессы добычи и переработки нефти газа и угля относятся к так называемым большим система или очень большим системам. Рассмотрим подробнее отличительные признаки больших систем
1.1.Очень большая система
Основные закономерности систем, их структуры и свойств мы рассматривают обычно на простых системах для облегчения их понимания. Кибернетика, однако, предусматривает возможность работы с системами значительно большей сложности - вычислительными машинами, сложными производствами, управляемыми вычислительными машинами, нервными системами, обществами. Прежде всего, определим, что мы понимаем под размерами системы. Главное, здесь не масса. Например, Солнце и Земля обладают очень большой массой, но с точки зрения систем, являются для нас достаточно малой системой, у них только двенадцать степеней свободы. Мы имеем в виду, скорее сложность системы. Но что означает сложность. Если рассматривать просто семью из пяти человек, то рассматривать ли ее как состоящую из пяти частей, т.е. довольно простую, или рассматривать как совокупность атомов в объеме 1023, т.е. очень сложную? В кибернетике «размеры» системы связываются с числом устанавливаемых различий; при этом имеется в виду либо число состояний системы, либо, если состояния системы определяются векторами, число составляющих вектора (т.е. число переменных системы или число ее степеней свободы). Эти две меры сложности взаимозависимы, ибо при прочих равных условиях введение новых, дополнительных переменных, делает возможными новые, дополнительные состояния. С функциональной точки зрения можно также увеличивать систему, если при неизменном числе переменных измерять каждую из них более точно, тем самым, обнаруживая у переменной больше различимых состояний.
Под сложностью системы мы будем понимать соотношение между системой и наблюдателем, изучающим ее свойства. Система будет считаться «очень большой» если она в каком-либо смысле слишком велика для детального изучения или управления ее состоянием, т.е. она превосходит возможности наблюдателя. Например, если систему молекул газа пытаться рассчитывать и различать ее состояния с помощью ньютоновской механики XIX века, число частиц в обычном объеме газа оказалось столь большим, что никакие практические наблюдения не смогли бы зафиксировать состояние системы и никакие практические вычисления не смогли бы предсказать ее будущее. Такая система была «очень большой» по отношению к физику XIX века. Животновод встречается с очень большой системой в генах, структуру которых он старается перестроить по новому образцу. Число генов и сложность их взаимодействия делают для него практически невозможным детальное управление ими. Металлург встречается с очень большой системой, когда он стремится наблюдать за протеканием всех элементарных реакций, имеющих место при выделении металлов из руды в процессе окислительной или восстановительной плавки.
Такие системы, слишком большие по отношению к современным средствам наблюдения и управления, весьма обычны в биологическом мире и его социально-экономических параллелях. Примером может служить и центральная нервная система.
Число нейронов в центральной нервной системе имеет порядок примерно 1010. И почти каждый из них возбуждается при многих воспоминаниях и мыслях. Во всех созданных человеком автоматах число частей колеблется в пределах от 103 до 107.
Однако следует заметить, что число элементов и размеры систем не нарушают тех общих принципов и свойств, которые были получены при рассмотрении систем с небольшим числом состояний. Особое преимущество метода, использующего состояния, а не обычные переменные, состоит в том, что он не требует явного упоминания о числе частей системы. Благодаря этому, доказанные однажды теоремы справедливы для систем любого размера. Применимость этих теорем к какой-либо реальной материальной системе может изменяться по мере того, как система становится очень большой. Однако о применимости можно говорить только по отношению к частным, конкретным случаям. Таким образом, размеры системы не лишают справедливости теорем и постулатов, доказанных при анализе небольших систем. Системный подход позволяет проводить изучение особенностей поведения большой системы с помощью анализа ее некоторой упрощенной модели.
Метод изучения природных явлений и процессов с использованием их моделей широко используется человечеством с древнейших времен. Моделью называют некий объект, отражающий основные, наиболее характерные черты изучаемого объекта, которые интересуют исследователя в данный момент времени. Например, если мы интересуемся особенностями движения объекта, то его моделью для этой цели может быть некая точка, характеризующая движение центра тяжести объекта под действием приложенной силы. Если мы хотим исследовать закономерности протекания нефти в магистральном нефтепроводе, то моделью такого объекта может быть трубка небольшого диаметра, по которой протекает жидкость, имеющая свойства, аналогичные свойствам нефти.
Таким образом, для исследования поведения объекта путем исследования его модели, необходимо, прежде всего, создать модель объекта. Модель должна отражать не все свойства объекта, а только те, которые интересуют исследователя в данный момент времени. Поэтому для одного и того же объекта могут быть разные модели, в зависимости от целей исследования.
Различают два основных вида моделирования:
1. Физическое моделирование.В этом случае физическая природа процессов, происходящих в модели и в объекте, одинакова и они отличаются только размерами или темпом процессов, происходящих в модели в объекте.
Например, если мы хотим исследовать закономерности протекания жидкости в трубопроводах большого диаметра, мы можем исследовать особенности течения жидкости в трубопроводах малого диаметра и обобщить полученные результаты на основе использования теории подобия.
Центральным положением этой теории является понятие подобия объектов, возникшее в геометрии и перенесенное в физику. По аналогии с геометрическим подобием вводится понятие физического подобия. Это может быть, например, гидродинамическое подобие (подобие потоков текучей жидкости), тепловое (подобие полей температур), механическое (подобие распределения сил, скоростей, энергетических характеристик), а позже кибернетическое (подобие процессов переработки информации в саморегулирующихся кибернетических системах). Основной постулат теории подобия гласит: правильные результаты при моделировании можно получить, обеспечив физическое подобие модели изучаемому объекту.
Первоначально понятие физического подобия рассматривалось лишь в отношении явлений и объектов одной физической природы. Например, потоки жидкости в моделируемом аппарате считалось обязательным воспроизводить лишь текучей жидкостью в малой геометрической копии аппарата. При этом часто возникала проблема подбора жидкости для модели. Пропорциональное изменение размеров необходимо было компенсировать в модели соответствующим изменением свойств жидкости. Затем понятие физического подобия было расширено. В это подобие стало возможным вовлекать и явления разной природы. А.А. Гухман предложил называть первый случай подобия физически однородных явлений – подобием в узком смысле, а второй, более общий случай - подобия для явлений различной физической природы – физической аналогией.
Фундаментальной является так называемая тройная аналогия процессов переноса: распространения тепла (теплопроводность), переноса массы (диффузия, фильтрация), перемещение электрического заряда (электрический ток). Законы переноса удается записать для перечисленных процессов единым уравнением, связывающим поток текучей субстанции (вещество, энергия) и проводимость среды. Все эти три явления, хотя имеют совершенно различную природу процессов, имеют одинаковое уравнение, описывающее эти процессы. Таким образом, это уравнение является математической моделью для этих процессов. Поэтому, изучая закономерности процесса переноса электричества, можно изучать явления переноса массы в аналогичных условиях. Таким образом, мы подошли к определению математического моделирования.
2. Математическое моделирование.В этом случае физическая
природа процессов, происходящих в модели и в объекте, может быть совершенно различна, но оказываются одинаковыми уравнения, описывающие изменение процессов в модели и в объекте.
Например, перенос вещества описывается законом Фика:
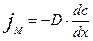 (1.2)
(1.2)
Перенос тепла описывается уравнением Фурье:
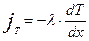 (1.3)
(1.3)
Перенос электричества описывается законом Ома:
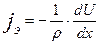 (1.4)
(1.4)
Все эти три уравнения имеют одинаковую структуру, они состоят из двух сомножителей, первый из которых является коэффициентом пропорциональности данного процесса, а второй является величиной градиента концентрации (с) температуры (Т), или напряжения (U) в направлении потока. Уравнения (1.2 – (1.4) являются математической моделью этих трех процессов, описывают их основные свойства – а именно, способность к переносу различных субстанций в поле распределения соответствующей величины в пространстве. Эти три процесса имеют одинаковую математическую модель и являются изоморфными. Каждое из трех рассмотренных явлений может быть моделью для исследований процессов переноса, описываемых моделью типа (1.2.)-(1.4). На этом основании можно, например, исследовать закономерности распространения вещества путем диффузии, исследуя закономерности распространения электрического тока в электропроводящей среде. Такой метод называется методом прямой аналогии. Он использовался при моделировании процессов на аналоговых вычислительных машинах. Метод прямой аналогии несет в себе черты подобия в узком смысле. При моделировании сложных объектов создание таких аналоговых моделей становится сложным, а сами модели становятся громоздкими и трудно реализуемыми, особенно для нелинейных систем.
Основополагающим принципом в моделировании является принцип изоморфизма: если две системы изоморфны, то каждую из них можно считать моделью другой. Однако так как модели отражают не все стороны явления или процесса, а только наиболее существенные с точки зрения исследователя, то и системы являются не полностью изоморфными, а только частично, по ограниченному объему свойств и характеристик. Такое неполное соответствие называют гомоморфизмом. Гомоморфизм также предполагает однозначное соответствие между объектами, но это соответствие не взаимно. Из гомоморфных объектов один обязательно моделируемый («натура»), а второй – модель. Их нельзя поменять местами, в отличие от изоморфных объектов.
При моделировании кибернетических систем можно соблюдать два вида подобия:
1) функциональное – совпадение функций систем в одинаковых условиях.
2) динамическое – совпадение между движением модели и объекта, т.е. между последовательно изменяющимися состояниями модели и объекта. Для различных целей моделирования объекту можно поставить в соответствие разные гомоморфные модели.
Пусть мы имеем две системы:
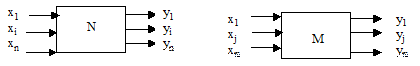 |
Рис.1.1. Сопоставление изоморфных систем.
Пусть
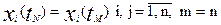 (1.5)
(1.5)
значения компонентов вектора входных переменных систем N и M, соответственно, а tN и tM темп протекания процессов в системах N и M
Если реакции этих систем также одинаковы:
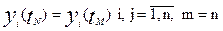 (1.6)
(1.6)
а течение времени в модели совпадает с натуральным:
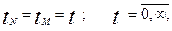 (1.7)
(1.7)
то системы M и N изоморфны. Но условия (1.5)-(1.7) очень «жесткие». Для их выполнения требуется, чтобы множества переменных состояния X и Y, совпадали в модели и в натуре, т.е. они должны включать все возможные в реальной системе воздействия и реакции на них. Темпы развития процессов в системах N и M должны совпадать. Поэтому всякий реальный объект является строго изоморфным только самому себе. Моделирование возможно только при упрощении условий (1.5)-(1.7). Прежде всего, необходимо уменьшить число компонентов у векторов XM и YM в модели по сравнению с моделируемым объектом. Это достигается тем, что в модели воспроизводятся не все свойства объекта, а только основные. Учитываются разные темпы протекания процессов в модели и в объекте. Это приводит к тому, что условия (1.5)-(1.7) могут быть записаны следующим образом:
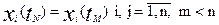 (1.8)
(1.8)
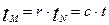 (1.9)
(1.9)
где r и с – коэффициенты пересчета масштаба времени. Введение масштабных коэффициентов времени позволяет изменить в модели темпы протекания процессов и сделать их более удобными для детального исследования. Наконец, условие (1.6) иногда целесообразно изменить следующим образом для удобства измерений на модели:
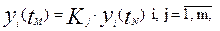 (1.10)
(1.10)
где 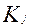 – множители изменения масштаба реакций системы на модели по сравнению с реакциями натуры; аналогичные изменения можно ввести в условие (1.8). Системы N и M, соответствующие условиям (1.8)-(1.10) , однозначно соответствуют друг другу, но это соответствие не взаимно. Система N (натура) всегда богаче по содержанию, чем система М (модель). Поэтому эти системы не изоморфны, но гомоморфны друг другу. Отсюда следуют следствия:
– множители изменения масштаба реакций системы на модели по сравнению с реакциями натуры; аналогичные изменения можно ввести в условие (1.8). Системы N и M, соответствующие условиям (1.8)-(1.10) , однозначно соответствуют друг другу, но это соответствие не взаимно. Система N (натура) всегда богаче по содержанию, чем система М (модель). Поэтому эти системы не изоморфны, но гомоморфны друг другу. Отсюда следуют следствия:
Следствие 1. Из того, что М есть модель N, не следует, что N моделирует М. .
Следствие 2. Сходство модели с оригиналом всегда неполное.
Следствие 3. Реальной системе на разных этапах ее исследования можно поставить в соответствие разные гомоморфные модели.
Используя полученные следствия и полученные выше соотношения, можно проводить разработку модели объекта и использовать ее для исследования поведения объекта на модели. В этом случае полученные результаты будут описывать поведение объекта с точностью, обеспечиваемой правильностью сделанных допущений.
Дата добавления: 2015-08-14; просмотров: 995;
