Минимизация по правильному симплексу

Поиск точки минимума функции 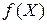с помощью правильных симплексов производится следующим образом. На каждой итерации поиска сравниваются значения функции 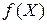в вершинах симплекса и выполняется процедура отражения для той вершины, в которой 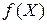принимает наибольшее значение. Если в отраженной вершине получается меньшее значение функции, то переходят к новому симплексу. Иначе выполняют ещё одну попытку отражения для вершины со следующим по величине значением 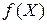. Если и она не приводит к уменьшению функции, то сокращают длину ребра и строят новый симплекс с этим ребром. При этом в качестве базовой выбирают ту вершину 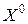старого симплекса, в которой функция принимает наименьшее значение. Поиск точки минимума 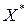заканчивают, когда либо ребро симплекса, либо разность между значениями функции в вершинах симплекса становятся достаточно малыми.

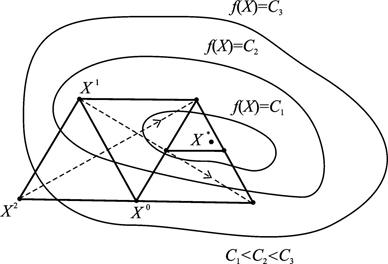
Геометрическая иллюстрация работы алгоритма в пространстве 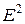показана на рис. 5.1, где точки 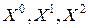- вершины начального симплекса, а пунктиром указаны операции отражения.

Рис. 5.1. Поиск точки минимума функции 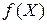с помощью правильных симплексов в пространстве .

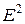Замечание 1. Следует иметь в виду, что если функция 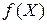многомодальна, то описанным методом может быть найдена точка локального, а не глобального минимума .

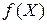Замечание 2.Если ограниченность целевой функции не очевидна, то в алгоритм метода следует включить дополнительную процедуру останова.