Прямые линии, параллельные одной из плоскостей проекций, называются прямыми уровня.

Среди них различают: прямую параллельную горизонтальной плоскости проекций (горизонтальная прямая уровня - горизонталь), которую обозначают буквой h (рис. 2.3);

прямую параллельную фронтальной плоскости проекций (фронтальная прямая уровня - фронталь), которую обозначают буквой f (рис. 2.4);

Прямую, параллельную профильной плоскости проекций (профильная прямая уровня), которую обозначают буквойр. (рис. 2.5).

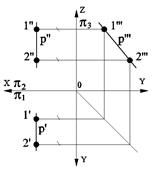
Рис. 2.3 Рис. 2.4 Рис. 2.5

Среди прямых, перпендикулярных к плоскостям проекций, выделяют:

горизонтально проецирующие прямые - прямые, перпендикулярные к горизонтальной плоскости проекций (рис. 2.6);

фронтально проецирующие прямые – прямые, перпендикулярные к фронтальной плоскости проекций (рис. 2.7);

профильно проецирующие прямые – прямые, перпендикулярные к профильной плоскости проекций (рис. 2.8).

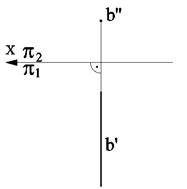
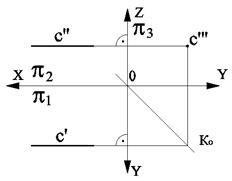
Рис. 2.6 Рис. 2.7 Рис. 2.8

2.2. ОПРЕДЕЛЕНИЕ НАТУРАЛЬНОЙ ВЕЛИЧИНЫ И УГЛОВ НАКЛОНА ОТРЕЗКА ПРЯМОЙ К ПЛОСКОСТЯМ ПРОЕКЦИЙ.

Натуральная величина отрезка прямой есть гипотенуза прямоугольного треугольника, катетами которого являются одна из его проекций и разность координат другой проекции отрезка относительно оси проекций (рис.2.9; 2.10). Этот прием называют “способом прямоугольного треугольника”.

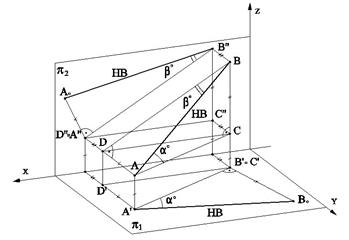
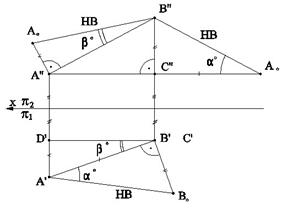
Рис. 2.9 Рис. 2.10

Измерение натуральной величины отрезка прямой можно выполнить одним циркулем-измерителем, если воспользоваться прямым углом между осью проекций и линией связи и отложить по сторонам этого угла проекцию отрезка, а по другой - разность координат концов другой проекции отрезка.