СИСТЕМЫ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ

§ 1.ОБЩИЕ СВЕДЕНИЯ

Последние десятилетия характеризуются колоссаль­ным ростом производительных и созидательных возможностей техники (использование атомной энергии в мирных целях, освоение космического пространства и т. д.). Такой пора­зительный прогресс человеческого интеллекта явился результа­том содружества человека с электронной вычислительной ма­шиной (ЭВМ), которое, сочетая в себе лучшие качества каж­дого из «партнеров», изменило облик науки и техники и ныне оказывает на них все возрастающее влияние.

Сказанное относится в первую очередь к использованию электронных вычислительных систем для проектирования слож­ных объектов. Это позволит не только сократить сроки разработки и снизить трудоемкость проектирования, но и найти более выгодные технические и экономические решения.

Автоматизация проектирования началась с наиболее просто­го—с чертежных, графических работ, а также с2耀ыполнения на ЭВМ стандартных инженерных расчетов.

Хотя автоматизация этих операций и важна, но она не дала качественного улучшения и существенного ускорения всего процесса проектирования сложных конструкций.

Если мы проанализируем проект какой-нибудь машины или устройства, то увидим, что наиболее труден первый шаг — завязка проекта, исходный замысел, эскиз. Чтобы выб­рать лучший вариант, проектировщик должен представить себе будущий объект в целом, увидеть, как он функциони­рует, оценить его слабые и сильные стороны.

Раньше конструктор мог справиться с этим самостоя­тельно. По мере усложнения создаваемых изделий станови­лось все труднее оценивать конкретный вариант проекта, его соответствие исходным требованиям; увеличивалось и число вариантов проекта, которые необходимо анализировать. Но производительность конструктора осталась практически неиз­менной и время проектирования возросло.

Выход из создавшегося положения дает изменение и упо­рядочение технологии проектирования. Усложнению конструк­ции и, как следствие, увеличению объема используемой кон­структором информации противопоставляют новые методы ее обработки, т. е. автоматизацию проектирования. В этом случае конструктор ставит задачу для ЭВМ и принимает окончательное решение, а машина обрабатывает весь объем информации и делает первичный отбор.

Для такого «общения» человека с машиной созданы и соз­даются системы автоматизированного проектирования (САПР), представляющие собой комплекс вычислительных устройств, средств связи, средств отображения, а также комплекс ма­тематических моделей, специальные языки программиро­вания и др.

Автоматизированное проектирование позволяет инженеру:

а) быстро проверить гипотезу и соответствующую ей модель (теоретическое или аналитическое представление проекта);

б) увидеть и немедленно исправить любые грубые ошибки в чертеже или в исходных утверждениях; в) оценить (путем сравнения с заданием) характеристики модели и модифици­ровать ее в многошаговом процессе совершенствования (оп­тимизации) конструкции; г) принять решение в критических точках ветвления и выбрать путь, по которому ЭВМ про­должит решение; д) управлять продвижением в решении задачи (окончить прогон, изменить входные данные и др.) и т. д.

Автоматизированноепроектирование избавляет проектиров­щика от трудоемких расчетов, позволяет больше времени от­давать творчеству, отысканию новых инженерных и научных решений.

В результате автоматизированного проектирования создает­ся эскизный проект изделия, содержащий его основные па­раметры, характеристики, схему конструкции и математическую модель изделия.

Автоматизированное конструирование осуществляет опти­мальный синтез конструктивных элементов с помощью ЭВМ.

При конструировании за основу принимается схема кон­струкции, полученная на этапе автоматизированного проекти­рования. Схема дополняется конструктивной разработкой от­дельных элементов (соединительных и переходных элементов, уплотнений и т. п.), проводится определение размеров, до­пусков и посадок и т. п.

В результате автоматизированного конструирования выпускается техническая документация, необходимая для технологи­ческой подготовки производства. Техническая документация содержит чертежи, получаемые на чертежных автоматах по раз­работанным программам, и технические условия (условия сбор­ки, контроля и т. п.). Вместе с тем в производство передается «машинный образ» конструкции в виде перфолент, содержащих программы для станков с ЧПУ (числовым программным управлением) для изготовления элементов конструкции.

Таким образом, новая технология проектирования — это система, которая начинается от замысла и кончается вы­дачей проектной документации или опытного образца.

В заключение отметим, что широкое применение ЭВМ при изготовлении и испытании изделий приведет со временем к автоматизированному производству, включающему в себя и первые его стадии: автоматизированное проектирование и автоматизированное конструирование.

§ 2. ОБЩИЕ ПРИНЦИПЫ ПОСТРОЕНИЯ СИСТЕМ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ

При создании систем автоматизированного проек­тирования (САПР) целесообразно использовать следующие об­щие принципы: 1) блочно-модульный; 2) иерархии; 3) адап­тации и развития; 4) информационного единства; 5) итерации.

Блочно-модульный принцип построения состоит в том, что система создается из отдельных самостоятельных частей блоков и модулей. Это существенно упрощает программи­рование.

Блоком системы проектирования называют ее часть, имею­щую функциональную определенность (например, блок огра­ничений, блок управления и т. д.).

Модули — наименьшие структурные элементы блока (мо­дуль определения контактных напряжений, расчета вращающего момента и т. п.).

Каждый из блоков системы выполняет определенные за­дачи, имеет свою входную и выходную информацию, сос­тавляется и доводится отдельно и только после этого вклю­чается в систему машинного проектирования. Блоки системы могут быть стандартными (например, блок решения системы уравнений и т. д.). Стандартные блоки инвариантны по от­ношению к элементам и узлам изделия и включаются в автоматические модели как стандартные элементы. При формировании таких блоков широко используется библиотека стандартных программ. Принцип иерархии моделей состоит в том, что каждая ма­тематическая модель включается как составная часть в модель более высокого класса.

Математическая модель детали входит в модель узла, которая, в свою очередь, включается в модель изделия.

Принцип иерархии отображает соотношения «старшинства», имеющиеся в любой сложной технической системе.

Принцип адаптации и развития требует, чтобы система машинного проектирования была согласованной со сложив­шейся практикой проектирования. Действующие методы рас­чета и проектирования, их программное обеспечение должны стать основной при разработке упрощенных и уточненных моделей.

Целесообразно, чтобы модели и их блоки, создаваемые для САПР, могли использоваться и независимо при прове­дении инженерных расчетов. Это ускорит и облегчит синтез сложных систем, разработку САПР.

Создаваемая система должна предусматривать возможность развития путем включения новых моделей и более широкого взаимодействия с другими системами.

Принцип информационного единства означает, что все пото­ки информации в системе должны быть совместимыми. Про­граммирование должно осуществляться на одном из универсаль­ных языков (например, на языке ПЛ-1 и ФОРТРАН). Тер­мины, условные обозначения, размерности физических вели­чин должны быть одинаковыми для всех систем.

При большом количестве действующих программ оказы­вается необходимым иметь управляющие программы. Для формирования таких программ и работы с ними удобно использовать проблемно ориентированные языки, специально приспособленные для системы автоматизированного проекти­рования. Они могут строиться двумя способами — с помощью дискрипторов (ключевых слов) и командных процедур или путем добавления специальных процедур в универсальные алгоритмические языки.

По принципу итерации система автоматизированного про­ектирования работает итеративно, т. е. путем последователь­ных приближений, постепенно уточняя и конкретизируя резуль­таты.

Общая схема функционирования системы показана на рис. 35.1. Сначала, исходя из потребностей старшей системы и предварительной оптимизации, формируются технические предложения для основных параметров изделия. Эти пара­метры поступают в линию анализа, где перерабатываются в более детальном виде технические характеристики раз­личных типов изделий и их конструктивных вариантов. Тех­нические условия для всего изделия позволяют указать тре­буемые параметры узлов и элементов, что дает возможность выбрать их конструктивные схемы, определить размеры, мас­су, габариты, провести их локальную оптимизацию. К этому следует добавить экономические оценки — стоимость проекти­рования, производства и эксплуатации будущего изделия.

После того как выяснен «облик» отдельных элементов, начинается синтез проекта, предусматривающий создание в па­мяти ЭВМ математической модели вариантов будущего изде­лия (в виде табличных зависимостей, соотношений и цифро­вой информации о размерах, массе и рабочих характеристи­ках отдельных элементов изделия). В процессе синтеза по тех­ническим характеристикам элементов уточняются параметры узлов и всего изделия и эти параметры поступают в блок оптимизации старшей системы. В блоке оптимизации вы­рабатываются указания по изменению параметров и харак­теристик изделия и их новые значения поступают в линию анализа для второй итерации (второго цикла) и процесс итерации продолжается. Такой подход к проектированию су­ществует лишь потому, что конструктору не известно заранее, как должен выполняться сразу синтез конструкции или проекта.

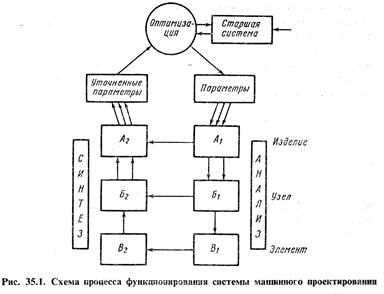
Конструктор умеет только анализировать пробный вариант проекта, изменять его параметры и таким образом строить процесс, сходящийся к решению.

Отметим следующую важную особенность итерационного процесса автоматизированного проектирования. Первые циклы процесса выполняются, как правило, только для упрощенных моделей. Уточненные модели используются при разработке проекта на стадиях технического задания и проектирования (когда выбран основной вариант конструкции).

§ 3. СТРУКТУРА МАТЕМАТИЧЕСКОЙ МОДЕЛИ

Математической моделью называют совокупность уравнений, условий и ограничений, описывающих функциони­рование элемента, узла или машины в целом.

Общая модель должна отражать следующие основные факторы: 1) работоспособность (взаимодействие с внешней средой и другими элементами); 2) энергетический баланс, коэффициенты полезного действия; 3) надежность (запасы прочности, долговечность); 4) экономическую эффективность (технологичность, стоимость производства и эксплуатации).

Например, при создании математической модели зубчатой передачи фактор работоспособности включает уравнение упру­гого контакта зубьев, уравнение равновесия и т. д.

Энергетический фактор содержит определение коэффициента полезного действия передачи.

Факторы надежности и экономической эффективности не требуют дополнительных пояснений.

Общая модель обычно содержит частные подмодели, от­ражающие отдельные факторы функционирования системы.

Структура математической модели в системе автоматизи­рованного проектирования показана на рис. 35.2.

Модель осуществляет преобразование входных параметров, отражающих условия нагружения, среды и т. д., в параметры выхода, характеризующие процессы и состояние самой системы.

Для пояснения блоков этой математической модели про­ектирования используем редуктор.

Для его модели входными параметрами могут быть:

1) требования к конструкции (сведения о потребности, прототип, усовершенствования действующих конструкций);

2) заданные параметры, в том числе параметры, прихо­дящие из модели более высокой системы — модели механизма (мощность, частота вращения, надежность, долговечность подшипников, материалы, средства обслуживания и др.); эти параметры являются не варьируемыми;

3) управляющие (внутренние) параметры, позволяющие осу­ществлять процесс оптимизации (число зубьев колес, ширина колес, передаточное отношение и др.).

Оптимизация осуществляется с помощью блока внутренней оптимизации. В этом блоке содержатся метод оптимизации, а также наиболее простые условия оптимизации (максимум КПД, минимум меж осевого расстояния или массы); эти па­раметры являются варьируемыми.

Важную роль играет блок ограничений, устанавливающий начальные значения варьируемых параметров, ширину шага варьирования, область поиска.

Блоки преобразования содержат блоки и модули, каждый /из которых осуществляет отдельную физически определенную часть преобразования (например, расчет усилий в зацеплении, расчет геометрических параметров передачи, учет упругой де­формации колес и валов, жесткость валов и шпоночных соединений, расчет подшипников, расчет стоимости с учетом машинного времени и стоимости материалов и др.).

Модель содержит банк данных, хранящий необходимую информацию (например, подшипники, материалы и их харак­теристики, заготовки, крышки и кольца, винты и болты, шпонки и т. д.).

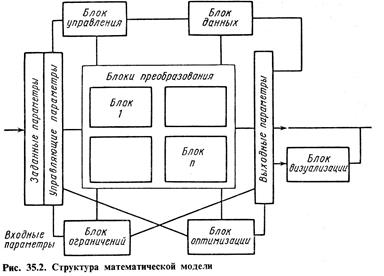
Имеется блок управления, воздействующий на управляющие параметры и осуществляющий переключение вариантов.

Модель включает блок выходных параметров, выдающий информацию (например, параметры зацепления, нагрузки, дав­ления, напряжения, рабочие чертежи, технологические карты, ведомость покупных изделий: подшипники, уплотнения и т. д., предварительная калькуляция: время обработки, стоимость, цифровая перфолента).

Модель содержит также блок визуализации, с помощью которого формируются изображения и графическая информация.

Все блоки модели связаны между собой, сама модель может являться частью более сложной модели.

Работа модели осуществляется по принципу последователь­ных приближений (итеративно). Сначала принимаются на­чальные значения управляющих параметров. Они вместе с за­данным параметром поступают в блок преобразований, где формируются параметры выхода. Выходные параметры на­правляются в блоки оптимизации и- ограничений, в которых вырабатываются указания об изменении исходных значений управляющих параметров. Далее переходят к следующему приближению, причем циклы продолжаются до завершения процесса оптимизации, о котором судят по критериям достаточности.

Окончательные результаты поступают в банк данных и на вход следующих моделей системы.

В заключение отметим, что в процессе проектирования создается большое число математических моделей отдельных процессов, элементов, узлов и т. п.

Для удобства программирования и общения модели услов­но делят на классы и уровни.

Класс моделиопределяется ее объемом (класс А — мо­дель изделия, класс Б — модель узла, класс В — модель де­тали).

Уровень моделихарактеризует глубину и полноту отобра­жения связей, существующих между параметрами входа и вы­хода. Для формирования моделей нулевого и первого уров­ней используется предшествующий опыт эксплуатации или простейшие теории (например, сопротивление материалов и др.). Модели более высоких уровней формируются на основе точных теорий (например, теории упругости, пластичности и др.).

В системе машинного проектирования целесообразно ис­пользовать модели нескольких уровней: более простые модели для предварительного отбора вариантов, более сложные — для формирования окончательной математической модели.

§ 4. ЦЕЛИ И МЕТОДЫ ОПТИМИЗАЦИИ

В задание на конструкторскую разработку включа­ют требование о том, чтобы при выборе проектных пара­метров некоторые главные характеристики изделия были оп­тимизированы.

Понятие оптимального решения подразумевает выбор ва­рианта конструкции с наибольшим числом преимуществ (на­пример, высокую надежность и быстродействие, малая масса а т. д.) и минимумом недостатков (например, низкий КПД, эольшие габариты и т. д.), т. е. речь идет о выборе наилучшего варианта среди множества возможных.

Уже при двух варьируемых параметрах бывает трудно уловить влияние каждого из них на главные характеристики. Возникает многомерная проблема. Чтобы такую проблему описать математически, задание должно быть соответственно обработано расчетчиком. Полный обсчет всех возможных ва­риантов проектных параметров часто произвести не удается. В этом случае эффективно использование методов оптимиза­ции, сокращающих время расчета, так как они выбирают кратчайшие пути оптимизации.

Укажем основной принцип оптимизации: оценка целесообраз­ности («качества») системы данного класса определяется эф­фективностью ее функционирования в системе более высо­кого класса. Например, качество ступени редуктора грузоподъ­емной машины следует оценивать по ее влиянию на Работу всего редуктора. В свою очередь, эффективность ре­дуктора должна оцениваться в системе более высокого клас­са (например, грузоподъемной машины и т. д.). Естественно, что по мере расширения класса цели оптимизации стано­вятся более общими, приобретая для очень больших систем социальный характер (условия оптимизации комплекса машин, транспортной системы и т. д.). Однако в практических рас­четах в большинстве случаев можно использовать локаль­ную или внутреннюю оптимизацию элементов, узлов и всего изделия, которая, как правило, оказывается полезной и для глобальной оптимизации. К числу целей локальной оптимиза­ции относятся: максимум экономичности (коэффициента по­лезного действия), минимум массы, минимум трудоемкости изготовления и др.

Допустим, что выбрана система обобщенных характеристик или параметров, характеризующих «качество» системы: g₁. g_2, g₃ …g

Условие оптимальности варианта можно записать в видеусловия экстремума некоторой целевой функции

w(: g₁. g_2, g₃ …g_r) = extremum.

В простейшем случае качество системы характеризуется одним параметром g₁. Тогда можно принять

w = g₁,