Напряженность поля прямолинейного проводника с током

Обозначим через R расстояние от проводника с током I до точки О, в которой определяется напряженность поля (рис. 6).

Выделим в проводнике элементарный участок dl на рассто­янии r от точки О. Так как для всех элементарных участков проводника сила тока I имеет одно значение, то полная напря­женность магнитного поля в точке О, согласно формуле (4) равна

Из точки О проведем радиусом г отрезок дуги АВ = r ∙ da. Вви­ду малости участка dl, а следовательно, и угла da, можно счи­тать, что отрезок АВ прямолинеен, а углы равны соответственно углу ABC = 90° и углу BCA = а. Тогда из ∆ ABC получим r ∙ da = dl-sin a, откуда

Вводя последнее выражение в формулу (6) и переходя от инте­грирования по длине к интегрированию по углу а в пределах от a₁ до а₂, получим

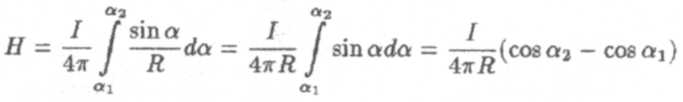
или окончательно

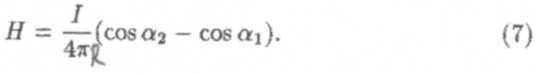
Формула (7) позволяет рассчитывать магнитное поле прямоли­нейного проводника с током конечной длины. Если проводник бесконечен, то a₁ → 0, а a₂ → 180°; тогда cos a₁ = 1, а cos a₂= -1. Подставим эти значения в формулу (7):

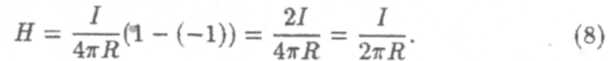
Полученная формула (8) выражает напряженность магнитного поля бесконечного прямолинейного проводника с током на рассто­янии R от проводника.