ЯЕО і молекулярний рух

Якщо взяти константи швидкості рівнянь (1.36) і підставити їх у рівняння (1.34), то можна побудувати криву, що наведена на Рис. 1.53. Вона являє собою залежність величини гомоядерного ЯЕО від швидкості молекулярного руху w_ot_c (де w_o – частота спектрометра, що приблизно дорівнює w_I і w_S). Варто нагадати, що це справедливо тільки для двохспінової системи з винятково диполь-дипольним механізмом релаксації, коли величина ЯЕО є максимальною. Крива містить три ділянки, які можна назвати областями швидкої, проміжної та повільної швидкості руху. Для молекул з великою швидкістю руху (короткі t_c і умова граничного звуження) ЯЕО має максимально можливе значення +0,5 або 50%. Такими молекулами є малі органічні молекули в нев'язких розчинниках, тому саме вони найчастіше вивчаються за допомогою стаціонарного ЯЕО. Інший граничний випадок - молекули з досить повільним рухом. Для них, як це було показано вище, характерним є негативний ЯЕО.

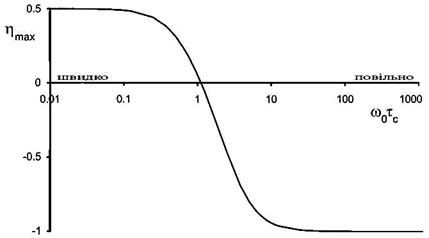
Рис. 1.53.Зміни максимального теоретичного гомоядерного стаціонарного ЯЕО у двохспіновій системі як функція швидкості молекулярного руху (задається безрозмірним параметром w_ot_c). Область швидкого руху відповідає граничному звуженню ліній. Область повільного руху відповідає межі спінової дифузії

Максимальна зміна інтенсивності сигналу для них відбувається у випадку, коли W₂ і W_I^I дорівнюють нулю. Якщо підставити ці значення в рівняння (1.34), то для ЯЕО одержимо величину –1 або –100%. Для вимірювання ЯЕО таких молекул слід використовувати нестаціонарні умови, оскільки за стаціонарних умов спектри виявляються неінформативними (див. нижче). У дану область попадають біологічні макромолекули. Їх традиційно вивчають у нестаціонарних умовах із застосуванням таких експериментів як NOESY. Між цими граничними випадками існує область проміжних швидкостей молекулярного руху. Тут ЯЕО змінює знак або навіть може дорівнювати нулю, коли W₀ = W₂. У цій області величина та знак ЯЕО виявляються досить чутливими до швидкості молекулярного руху, однак їхні величини можуть бути занадто слабкими для надійних структурних кореляцій. Розташування області проміжних швидкостей руху залежить від багатьох факторів - розміру та форми молекул, властивостей розчину (в'язкість, температура, іноді рН) і сили поля спектрометра. Найчастіше в даний діапазон попадають молекули з молекулярною масою 1000-2000 Дальтон. З підвищенням інтересу хіміків до великих молекул, зокрема до супрамолекулярної хімії все більша кількість молекул попадає до діапазону проміжних швидкостей руху, для якого виникають складності при використанні ЯЕО. Графік на Рис. 1.53 проходить через нуль у випадку, коли швидкість молекулярного руху приблизно дорівнює частоті спектрометра.

Таким чином, величини ЯЕО в значній мірі залежать від частоти спектрометра. Це ілюструє Рис. 1.64, де залежність величини ЯЕО від часу кореляції наведена для трьох різних магнітних полів. Використання сильних магнітних полів підвищує ймовірність попадання малих молекул в область проміжних швидкостей руху, а молекул середнього розміру в область повільних рухів. Тому використання магнітів із сильними полями завжди сприяє дослідженню великих молекул, оскільки для них зростає вірогідність переходу в область негативних ЯЕО, але вивчення малих молекул в сильних магнітних полях методом ЯЕО може виявитися неефективним через перехід цих молекул в область нульових ЯЕО.

Швидкість руху молекул можна до деякої міри регулювати за допомогою зміни умов експерименту. Найбільш просто із цією метою вимірювати спектри при різних температурах. Ще один можливий підхід - вимірювати спектри в системі координат, що обертається. Даний підхід буде описаний пізніше, відзначимо тільки, що в цьому випадку всі ЯЕО виявляються позитивними для будь-яких швидкостей молекулярного руху, тому знімається проблема нульової крос-релаксації.

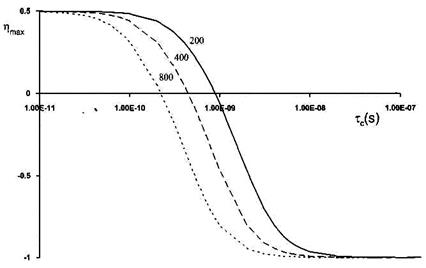
Рис. 1.54.Зміни максимального теоретичного гомоядерного стаціонарного ЯЕО у двохспіновій системі як функція швидкості молекулярного руху, показані для трьох частот спектрометра (MГц)