ЯЕО у двохспіновій системі.

Нехай речовини містить тільки два однакових ядра зі спіном ½, I і S, які перебувають у жорсткій молекулі, що розчинена в ізотропному розчині. У такому випадку не існує якоїсь переважної осі обертання і молекула обертається ізотропно, тобто відсутня вісь переважного обертання молекули. За таких умов між ядрами відсутня скалярна спін-спінова взаємодія через простір (J_IS=0), однак вони розташовуються достатньо близько одне від одного для наявності взаємодії між їхніми магнітними моментами, тобто для диполярної взаємодії. При цьому кожний зі спінів відчуває орієнтацію партнера по взаємодії. Тут ситуація цілком аналогічна до тієї, що спостерігається для двох точкових магнітів, які розташовані один біля одного. Описати таку систему, якщо вважати, що зразок містить 4N молекул можна за допомогою енергетичної діаграми.

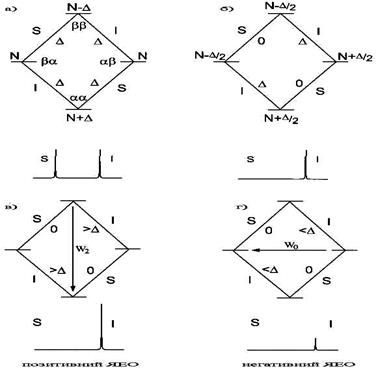
Рис. 1.51.Діаграми енергетичних рівнів і різниці населеностей для двох спінів, S і I, між якими є диполярна взаємодія; (a) у рівновазі, (б) після насичення спіна S, (в) після релаксації за допомогою процесу W2 і (г) після релаксації через шлях Wo Внизу показані спектри, що відповідають кожному варіанту.

Діаграма енергетичних рівнів для ансамблю 4N молекул показана на Рис. 1.51. Оскільки ми розглядаємо гомоядерну систему, то енергії переходів спінів I і S будуть практично ідентичними (різниця хімічних зсувів в порівнянні з Ларморовою частотою є настільки малою, що нею можна знехтувати) і можна вважати, що стани ab і ba у рівновазі однакові за енергією. Відповідно до розподілу Больцмана, є надлишок ядер на нижньому енергетичному рівні (aa) і деякий дефіцит на більш високому рівні (bb). Оскільки нас цікавить тільки зміна населеностей енергетичних рівнів, то позначимо надлишок ядер на нижньому рівні як D. Тоді дефіцит ядер на верхньому рівні буде –D. (у порівнянні з рівнями ab і ba). Відзначимо, що диполярні взаємодії не приводять до виникнення видимих розщеплень сигналів у розчинах, тому обидва переходи, що пов'язані з одним спіном, ідентичні за енергією. Тому за відсутності додаткового опромінення, спектр містить два синглети однакової інтенсивності (Рис. 1.51а).

Тепер припустимо, що ми насичуємо сигнал S. Це означає, що спіни S здійснюють швидкий перехід між можливими для них енергетичними станами. При цьому різниця населеностей для переходів ядра S дорівнюватиме нулю. Отриманий при цьому розподіл населеностей показаний на Рис. 1.51б. Видно, що система вийшла зі стану рівноваги і різниця населеностей між рівнями змінилася. Тому система буде прагнути відновити рівноважну населеність. Зміна спінових станів може відбувається під впливом процесів поздовжньої релаксації. У зв'язку із цим слід вирішити, які саме релаксаційні процеси сприятимуть встановленню рівноваги. Якщо ігнорувати механізми релаксації, можна передбачати 6 можливих шляхів релаксації двохспінової системи (Рис. 1.52).

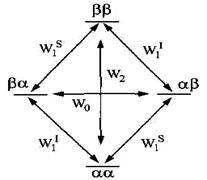
Рис. 1.52.Шість можливих переходів для двохспінової системи.

Чотири з них відповідають одноквантовим переходам, у яких відбувається перескок тільки одного спіна, наприклад aa-ba. Імовірність кожного переходу або швидкість, з якою здійснюється перескок спіна по даному шляху позначимо W. Два шляхи, що залишилися відповідають перескоку двох спінів одночасно, ab-ba і aa-bb. Хоча ці переходи і існують, їх, на відміну від одноквантових переходів, неможливо побачити прямо в експерименті ЯМР, оскільки в цьому випадку загальна зміна магнітного квантового числа (DM) не дорівнює одиниці. Говорять, що ці переходи заборонені квантово-механічними правилами відбору. Процес ab-ba з імовірністю W_o відповідає нуль-квантовому переходу (DM=0), а процес aa-bb з ймовірністю W₂ - двохквантовому переходу (DM=2). Але, хоча такі переходи не відбуваються при поглинанні енергії, при релаксації обидва шляхи можуть бути реалізованими. Для ЯЕО вони виявляються найбільш важливими. Їх називають шляхами крос-релаксації. Термін підкреслює участь у релаксації одночасно обох спінів.

Вертаючись до діаграми, що наведена на Рис. 1.52, ми зараз зупинимося на питанні про те, як різні релаксаційні процеси можуть сприяти відновленню рівноваги, якщо врахувати, що перехід W₁^S ми продовжуємо насичувати постійним радіочастотним опроміненням. Різниця населеностей між переходами спіна I, як і раніше, дорівнює D, оскільки для цього спіна рівноважні умови зберігаються. Тому шлях W₁^I не відіграє ролі у відновленні рівноваги і, відповідно, у виникненні ЯЕО. Процес W₂ переводить спіни зі стану bb у стан aa і тим самим відновлює різницю населеностей між переходами спіна S. При цьому різниця населеностей між рівнями спіна I зростає (Рис. 1.51в). Таким чином, результатом здійснення релаксації через шлях W₂ є загальне зростання інтенсивності в спектрі сигналу I. Таким чином, при цьому з'являється позитивний ЯЕО. Аналогічно, процес W_o приводить до переходу спінів зі стану ba у стан ab. При цьому відбувається відновлення населеностей спіна S. Результатом є зменшення різниці населеностей спіна I (Рис. 1.51г). Тому релаксація за шляхом W_o приводить до загального зменшення інтенсивності сигналу спіна I. Це негативний ЯЕО.

Виходячи з наведених вище якісних описів, ми можемо зрозуміти, чому виникає явище ЯЕО. В загальному випадку, процеси крос-релаксації W₂ та W_o відбуваються одночасно і спостережуваний знак ЯЕО визначається тим, який шлях для даної системи є більш ефективним.

Крім того, шлях W₁^I після того, як виникне ЯЕО, починає сприяти відновленню рівноважної населеності переходів спіна I, тому він зменшує величину ЯЕО. Внаслідок цього, якщо механізм W₁^I виявляється більш ефективним, ніж механізми крос-релаксації, то ЯЕО може стати настільки малим, що може не спостерігатися. Таким чином, виміряний ЯЕО є результатом балансу декількох конкуруючих шляхів релаксації. Насичення спіна S протягом періоду часу, більшого за час його релаксації, приводить до нових стаціонарних населеностей рівнів, які визначають інтенсивності сигналів в отриманому спектрі. Повний аналіз всіх шляхів релаксації і змін населеностей, що виникають при цьому, дозволяє розрахувати величину ЯЕО. Це т.зв. рівняння Соломона:

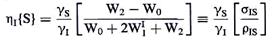(1.34)

Множник s_IS являє собою швидкість крос-релаксації двох спінів, а r_IS відповідає загальній швидкості диполярної поздовжньої релаксації спіна I. Для врахування впливу на населеності гіромагнітних відношень взаємодіючих ядер, в рівняння включені їх величини (g_S і g_I). Для гомоядерної системи, що обговорювалася вище, ці величини однакові і можуть бути виключеними з рівняння. Це загальне рівняння включає і якісні критерії, що описані вище, наприклад, W₂ – W₀ визначає знак ЯЕО, а W₁^I відповідає конкуруючому процесу релаксації, що зменшує величину ЯЕО. Для того, щоб знайти величину та знак ЯЕО необхідно знати, як впливають на швидкість різних релаксаційних процесів молекулярна рухливість і відстані між спінами. Саме цим питанням буде присвячене наступне обговорення.

Для нуль-квантового процесу W_o різниця енергій спінових станів досить мала. Вона відповідає різниці частот поглинання спінів I і S. Тому w_t = (w_I – w_S). Такі частоти виникають винятково у випадку повільного обертання молекул. Двохквантові переходи W₂ відповідають сумі частот поглинання спінів I і S. Тому w_t = (w_I + w_S). Такі частоти стимулюються швидким обертанням молекул. Для приклада розглянемо гомоядерну спінову систему при частоті спостереження в 400 МГц. Частоти одноквантових переходів W_I^I і W_I^S будуть дорівнювати приблизно 400 МГц. Частота переходу W_o відповідає різниці частот поглинання спінів I і S, тобто різниці їхніх хімічних зсувів. Вона лежить у діапазоні від Гц до кГц. Частоти переходів W₂ відповідають сумі частот переходів спінів і близькі до 800 МГц. Зрозуміло, що швидкість молекулярного руху, яка може стимулювати такі переходи повинна бути досить великою. Таким чином, для молекул з високою швидкістю обертання слід очікувати позитивних ЯЕО, що обумовлені крос-релаксацією за шляхом W₂, а для молекул, що обертаються повільно, повинні реалізовуватися негативні ЯЕО за рахунок підвищення ефективності шляху W_o. Це й відбувається на практиці.

Кількісні співвідношення для швидкостей диполярної релаксації у двохспіновій системі мають вигляд:

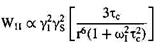(1.35а)

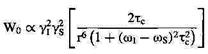(1.35б)

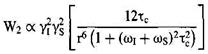(1.35в)

Константи пропорційності у всіх випадках однакові.

Відзначте, що на додаток до залежності від часу кореляції, ці рівняння містять величину між’ядерної відстані, r між спінами I і S. Оскільки у формулу цей параметр входить у шостому ступені, то кількісні розрахунки на підставі ЯЕО слід робити з великою обережністю. Множник між’ядерних відстаней описує величину диполярної взаємодії між спінами. Важливим тут є те, що всі шляхи релаксації однаково залежать від між’ядерних відстаней. Це, як буде показано нижче, дозволяє проводити кореляцію величин ЯЕО зі структурою молекул. Те, що величина ЯЕО є обернено-пропорційною до шостого ступеня між’ядерної відстані, свідчить про швидкий спад ефекту. Помітні ЯЕО спостерігаються між протонами, що відокремлені один від іншого не більше ніж на 0,5 нм (звичайно, це залежить від чутливості спектрометра і від того, наскільки точно можна вимірювати інтенсивності сигналів). Слід також пам'ятати про наявність у рівняннях (1.35) величин гіромагнітних відношень взаємодіючих спінів. Тому в гетероядерній системі величини швидкостей релаксації і, відповідно, ЯЕО можуть бути суттєво різними.

Якщо молекула в розчині обертається настільки швидко, що wt_c<<1, то всіма множниками, що містять w, можна знехтувати. Вирази для швидкостей релаксації при цьому спрощуються:

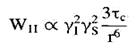(1.36а)

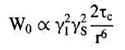(1.36б)

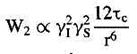(1.36в)

Ця ситуація називається умовою граничного звуження ліній, оскільки при цьому всі уширення сигналів, що пов'язані з диполярною взаємодією, усереднюються до нуля. Така ситуація має місце тільки при вимірюванні спектрів малих молекул у нев'язких розчинниках. Дотримання умов граничного звуження залежить від часу кореляції молекули та від напруженості магнітного поля спектрометра.