В СТАРШЕМ ДОШКОЛЬНОМ ВОЗРАСТЕ

В старшем дошкольном возрасте и в первом классе с целью развития у детей углубленных, обобщенных представлений о натуральных числах и натуральной последовательности на специальных занятиях решаются следующие образовательные задачи:

1. Учить сравнивать числа на основе использования предметных (игрушки, предметы быта), графических (линии, стрелки, круги Эйлера) и символических (цифры, знаки) моделей, постепенно переходя к сравнению чисел без опоры на наглядный материал.

2. Формировать на этой основе представления о постоянстве связей между рядом стоящими числами: 5 всегда больше 4, 4 всегда меньше 5.

3. Учить видеть постоянство разности между рядом стоящими числами: 5 больше, чем 4 на 1; 4 меньше, чем 5 на 1.

4. Познакомить с взаимно обратным характером отношений между рядом стоящими числами: 4 больше 3 на 1, но если к 3 прибавить 1, то получится 4; 5 меньше 6 на 1, но если из 6 убрать 1, то получится 5.

5. Показать относительность понятий «больше», «меньше» (5 меньше 6, но больше 4) и транзитивность отношений «больше», «меньше» (1 меньше 2, 2 меньше 3, значит, 1 меньше 3).

6. Сформировать представление о последовательности чисел натурального ряда.

7. Продолжать учить обозначать результат действий с помощью слов «больше (на)», «меньше (на)» и знаков < , > , =.

Работа с детьми проводится по двум образовательным направлениям одновременно. Первое направление – расширение и уточнение представлений детей о связях и отношениях между числами на основе сравнения чисел, второе – знакомство с принципом образования чисел первого десятка, формирование представлений о натуральном ряде чисел.

Первое направление – сравнение чисел первого десятка

Сравнить рядом стоящие числа – это значит определить, какое из них больше, а какое меньше. Установить разностные отношения – значит определить, на сколько одно число больше или меньше другого. При сравнении двух чисел меньшим считается то, которое при счёте называется раньше, а в натуральном ряду стоит левее.

Сравнивать числа с опорой на наглядный материал дети начинают уже в средней группе в процессе освоения механизма счётной деятельности. В старшей группе эта образовательная задача становится самостоятельной.

При изучении чисел второго пятка, кроме работы с двумя рядами пособий, направленной на выявление принципа образования следующего и предыдущего числа, необходимо включать дополнительные упражнения.

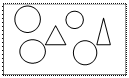
Воспитатель демонстрирует две группы фигур: 4 круга и 2 треугольника. Спрашивает у детей: «Каких фигур больше?». Этот вопрос не вызывает затруднений, поскольку ответ визуально ясен.

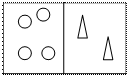Затем показываем на моделях другую ситуацию: «Где – справа или слева – фигур больше?». Ответ визуально не ясен, нужно выяснить это (или подтвердить предположение о соотношении по количеству). Дети предлагают различные варианты для сравнения: посчитать, составить пары, соединить линиями и на этой основе сравнить числа. Выясняем, что 7 больше 6, а 6 меньше 7.

Числа 7 и 6 рассматриваются ещё на трех-четырех видах наглядного материала, на этой основе делается обобщение: 6 всегда меньше 7, а 7 всегда больше 6. Такая работа проводится со всеми рядом стоящими числами в пределах 10.

Далее вводится символическая модель:

Gt; 6

Постепенно подводим детей к сравнению чисел без опоры на наглядный материал, предметные модели используются для проверки, подтверждения выявленных отношений. Дети сравнивают множества предметов по количеству элементов, оперируя только отношениями между числами: «Чего больше, кругов или квадратов? – Кругов больше, так как кругов 7, а квадратов 6, 7 всегда больше 6, а 6 всегда меньше 7».

Полезно провести упражнения: «Говорящие стрелки», «Разговор чисел». (Ж.Папи, Ф.Папи. «Дети и графы»).

1 2

3 4

Второе направление – образование чисел, натуральный ряд

В процессе освоения механизма счёта дети делают первые шаги в освоении принципа образования числа и натурального ряда. Специально эту работу проводят в старшем возрасте. Рассмотрим примеры упражнений.

На наборном полотне выставляются три ряда пособий: по 6 цветов, флажков и кубиков. Вопросы и действия:

· Сколько цветов? Посмотрите, что я сделаю (добавить один цветок). Больше или меньше цветов стало? Сколько стало цветов? Как получили 7 цветов?

· Сколько флажков? Если я добавлю ещё один флажок, сколько их станет? Как получили 7 флажков?

· Сколько кубиков? Что надо сделать, чтобы получилось 7 кубиков?

· Как получилось число 7? (к шести добавили один)

Те же действия выполняем в обратном порядке, обобщаем, как из числа 7 получить число 6.

{{{{{{{ ï {

OOOOOOO

rrrrrrr

Уже при знакомстве с числами первого десятка необходимо вместе с детьми строить числовую лесенку: «Чтобы построить лесенку, я возьму один круг (квадрат), это будет первая ступенька. Рядом я поставлю столько же кругов да ещё один. Это будет следующая ступенька. Сколько я взяла кругов? Как получилось число 2? Как построить следующую ступеньку?» и т.д.

1 2 3 4

Вопросы для работы с лесенкой:

· Как получили число 5?

· Какое число больше, 6 или 5? Какое число меньше, 5 или 6?

· Как узнали?

· На сколько 5 меньше, чем 6?

· Как получить из числа 5 число 6?Из 6 пять?

· Какое число получится, если к 5 добавить 1, из 5 убрать 1?

· Какое число больше, чем 5 на 1?

Таким образом, необходимо рассмотреть все свойства рядом стоящих чисел. Числовая лесенка позволяет соотнести цифру и количество – для этого разместите цифры под соответствующими столбцами. На основе этой модели дети получают первые представления о натуральной последовательности.

На основе знаний о цифрах дети вместе с воспитателем составляют натуральный ряд чисел (отрезок) через постепенное (по одному) предъявление предметов и их обозначение цифрами: воспитатель выставляет предмет, просит найти и выложить перед собой соответствующую цифру; добавляет ещё один предмет и так далее. На полочке (наборном полотне) появляется ряд предметов, а перед ребёнком – ряд цифр, расположенных в возрастающем порядке.

¶ ¶ ¶

1 2 3

На основе подобных упражнений дети учатся различать понятия до, после, предыдущее, последующее число, стоит перед, следует за: «Положили одну звездочку, сколько звёздочек? Какую цифру надо положить? Сколько будет звёздочек, если я положу еще одну? Какое следующее число вы назовете? Какую цифру надо положить? Сначала вы положили цифру 1, потом – цифру 2. 1 стоит перед числом 2, 2 – после числа 1, следует за ним. 1 стоит до числа 2, 2 – после числа 1. 1 – предыдущее число, 2 – последующее число».

Для формирования умения различать выделенные понятия используем упражнение «Лягушонок».

«Это кочки на болоте. По ним весело прыгает Лягушонок. Он хорошо знает числа и цифры и поможет нам выполнять разные задания». Далее воспитатель (а потом и дети) придумывают задания, которые выполняет вызванный ребёнок, перемещая фигурку Лягушонка по кочкам. Например: «Найти число 6. Посадить Лягушонка на предыдущее число. Найти число, больше чем 6 на 1. Найти число, стоящее перед числом 5; после числа 8; следует за числом 3. Найти левого соседа у числа 7» и т.д.

Упражнение «Сказочные цифры». Оно может использоваться как диагностическое – понимание детьми принципа построения натурального ряда чисел и механизма образования числа.

Детям предлагается таблица (бумажная лента) со сказочными цифрами, которые учат дети в сказочной школе: «Сказочные цифры не похожи на наши, но расположены в ряду так же: слева – меньшее число, справа – большее. Слева направо каждое следующее число больше предыдущего на один. С помощью этих цифр дети решают задачи в сказочной школе. Давайте и мы попробуем их тоже решить.

- Гномик Митя в красной шапочке нашёл столько (показывается красной стрелочкой любой знак в таблице) грибов, а гномик Мотя в синей шапочке – вот столько(показываем стрелкой синего цвета). Кто нашел больше грибов? Как догадались?

- Гномик Сеня нашел столькогрибов, гномик Соня подарила ему ещё один гриб. Покажите, сколько стало грибов у гномика Сени. Почему?

- Красная Шапочка принесла бабушке к ужину вот столько пирожков. Бабушка съела один и очень похвалила Красную Шапочку. Покажите, сколько осталось пирожков у бабушки для завтрака. Как узнали?

- Какое число больше: это или это? Как догадались? На сколько?»

В старшем возрасте детей необходимо познакомить с числовым лучом, который моделируется в совместной деятельности. При этом внимание детей фиксируется на принципе расположения чисел, способе их записи, обозначении.

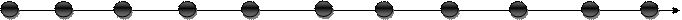
0 1 2 3 4 5 6 7 8 9 10

Предлагаются упражнения «Быстро найди число», «Назови соседей числа», «Называй числа дальше», «Выбери ряд чисел, которым можно пользоваться при счёте», «Какое число пропущено?», «Разложи по порядку», «Путаница», «Найди ошибку», «Продолжи ряд», «Разгадай закономерность». Предлагаем выложить цифровую цепочку», которая изготавливается по типу пазлов.

В старшем дошкольном возрасте стоит задача – научить детей называть числа в обратном порядке (такая формулировка связана с тем, что процесс счёта носит векторный характер в сторону увеличения числа). Число, названное при счёте последним, является ответом на вопрос сколько?

Обучение ведется на наглядном материале. Сначала выставляем перед детьми четыре предмета (уточнить, сколько их). Затем предметы убираем по одному, справа налево, при этом просим детей вслух называть, сколько предметов остаётся. Таким образом, мы слышим последовательно уменьшающийся ряд чисел: 4, 3, 2, 1.

Далее учим называть числа в обратном порядке со зрительной опорой на числовой луч.

Полезно для закрепления предлагать задания, в которых требуется называть числа в обратном порядке. Например, «Как почтальону быстрее отнести письмо в дом № 6?» Удобнее искать его справа налево, дорога будет короче.

H H H H H H H H H