Расчет рекуперативных Теплообменных аппаратов.

Существуют следующие виды расчетов: проектный и поверочный. Проектный, в свою очередь, включает в себя тепловой конструктивный, компоновочный, гидравлический, механический и техникоэкономический расчеты.

Целью теплового конструктивного расчета является определение площади поверхности теплообмена 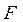аппарата.

В компоновочном расчете устанавливают основные соотношения между линейными размерами, площадью поверхности теплообмена и проходными сечениями каналов, число ходов, габаритные

размеры теплообменника с учетом требований ГОСТов.

При гидравлическом расчете определяют гидравлические сопротивления теплообменника и затраты мощности на перемещение

теплоносителей.

Механический расчет – это проверка деталей теплообменника

на прочность, плотность и жесткость.

Поверочный расчет производится для установления возможности использования имеющегося или выбираемого стандартного аппарата в заданных условиях; для расчета режимов работы, отличных от номинальных.

Тепловой конструктивный расчет рекуперативных теплообменников сводится обычно к совместному решению основного уравнения теплопередачи.

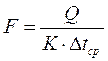(3.1.1.1)

и уравнения теплового баланса

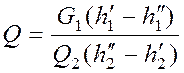(3.1.1.2)

где 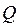– тепловая нагрузка аппарата, Вт;

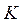– коэффициент теплопередачи,Вт /(м2 · К);

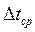– средний температурный напор, град;

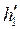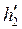, – энтальпии соответственно греющего и нагреваемого теплоносителей на входе в аппарат, Дж/кг;

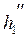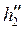, – энтальпии соответственно греющего и нагреваемого теплоносителей на выходе из аппарата, Дж/кг;

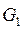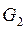и – расходы соответственно греющего и нагреваемого теплоносителей, кг/с.

Уравнение теплового баланса (3.1.1.2) записано без учета потерь .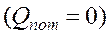

Если фазовые превращения теплоносителей отсутствуют, то ;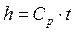

здесь 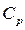и 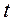– удельная изобарная теплоемкость, Дж/кг · К и температура (°C) теплоносителей соответственно.

Средний температурный напор при прямотоке и противотоке (рис. 3.1.1.1.) при условии, что температура обоих теплоносителей изменяется вдоль поверхности нагрева, определяется как среднелогарифметический (если ):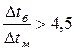

(3.1.1.3)

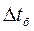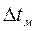где и – соответственно наибольшая и наименьшая разности

температур.

При 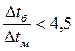пользуются упрощенной формулой

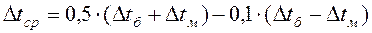. (3.1.1.4)

Если 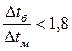– зависимость .

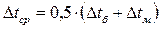При фазовых изменениях теплоносителей в аппарате средний температурный напор определяется как разность температур насыщения теплоносителей при их давлениях:

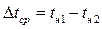. (3.1.1.5)

При этом температура обоих теплоносителей вдоль поверхности

нагрева не изменяется.

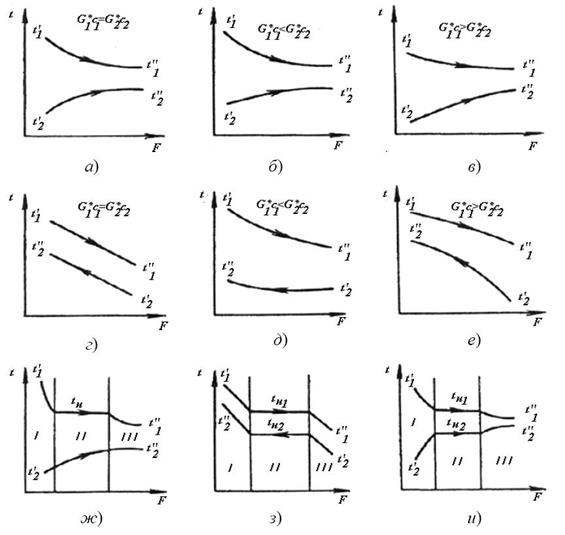
Рис. 3.1.1.1. Графики изменения температур в теплообменниках:

а, б, в – при прямотоке; г, д, е – при противотоке; ж – при изменении

фазового состояния ( конденсации) греющего теплоносителя;

з, и – при изменении фазового состояния обоих теплоносителей

Средняя разность температур для более сложных схем движения

теплоносителей, не меняющих агрегатного состояния, рассчитывается

следующим образом:

1) определяется средний температурный напор по формуле (3.1.1.3),

2) находят величины

Средний температурный напор находится как

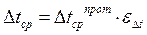
где 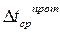– температурный напор, рассчитанный по формуле (3.1.1.3).

Коэффициент теплопередачи 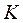представляет собой количественную

расчетную величину, характеризующую сложный теплообмен и зависящую от многих факторов (температур, температурных напоров, скоростей движения теплоносителей, давлений, физических параметров и т. д.):

– для плоской стенки:

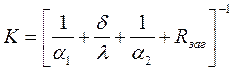; (3.1.1.6)

– для цилиндрической:

, (3.1.1.7)

где 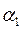и 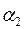– коэффициенты теплоотдачи горячего и холодного теплоносителей; Вт/м2 · К;

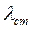– коэффициент теплопроводности материала стенки, Вт/м · К;

– термическое сопротивление, учитывающее загрязнение с обоих сторон стенки, м2 · К/Вт;

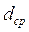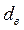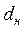, , – средний, внутренний и наружный диаметры труб, м;

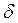– толщина стенки, м.

Средний диаметр 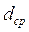определяется следующим образом:

при ;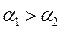

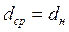при ;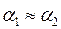

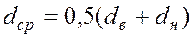при .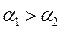

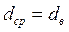Если отношение 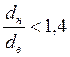, то расчет коэффициента теплопередачи ведут по формуле (3.1.1.6) для плоской стенки.