Гипербола и ее каноническое уравнение

Лекция 3

Линии второго порядка, заданные каноническими уравнениями

Гипербола и ее каноническое уравнение

Определение. Гиперболой называется геометрическое место точек, для каждой из которых абсолютная величина разности расстояний до двух фиксированных точек плоскости, называемых фокусами, есть данное положительное число 2а, меньшее, чем расстояние 2с между фокусами.

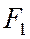Пусть - произвольная точка гиперболы, а и 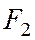- ее фокусы. Отрезк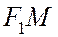и и 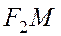так же, как и их длины, называются фокальными радиусами гиперболы. Поэтому

(1)

Введем на плоскости прямоугольную систему координат, принимая середину отрезка 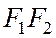за начало координат, а за ось Ох – прямую 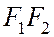, ориентированную от точки 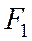к точке 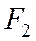. В выбранной системе координат фокус 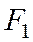имеет координаты 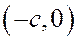, а фокус 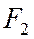- координаты . Обозначая координаты точки М гиперболы через х и у, будим иметь

,

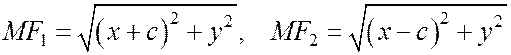и соотношение 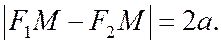принимает вид

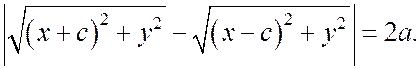
Преобразуем это уравнение. Раскрываем модуль ,

.

Дважды возводим в квадрат, получим:

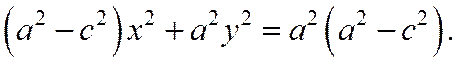
Однако, теперь 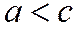. Обозначая разность 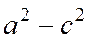через :

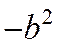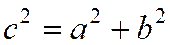, (2)

имеем: ,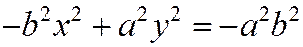

или 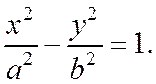(3)

Итак, координаты любой точки гиперболы удовлетворяют уравнению (3):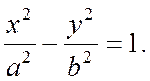

Докажем обратное. Если координаты некоторой точки М(х, у) удовлетворяют уравнению (3), то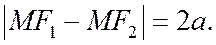

Для этого найдем расстояние и 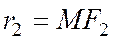от этой точки до точек 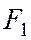и :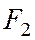

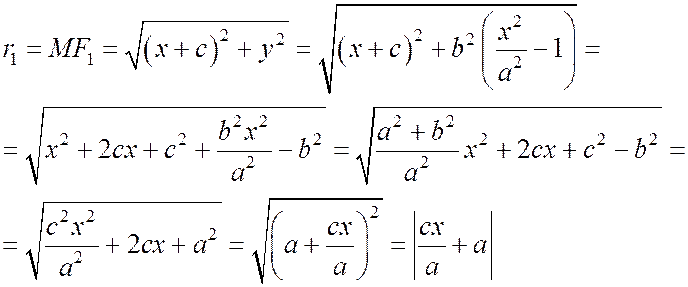
и аналогично .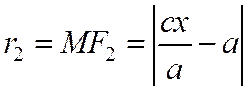

Из равенства

Следует, что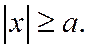

Если 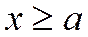, то в силу соотношения 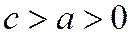будем иметь ,

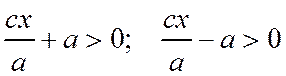а потому 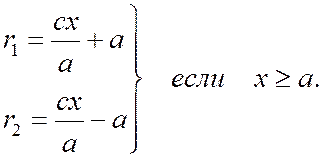(4)

Если же , то

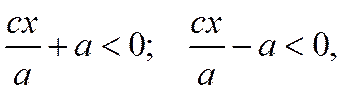
а потому 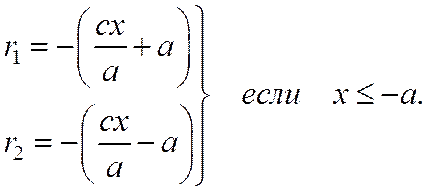(5)

Таким образом, если ; то 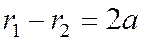, а если 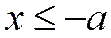, то 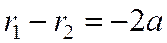, в обоих случаях

.

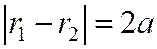Итак, мы доказали, что координаты любой точки гиперболы удовлетворяет уравнению

,

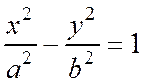и обратно: если координаты точки удовлетворяют этому уравнению, то эта точка лежит на рассматриваемой гиперболе.

Следовательно, уравнение

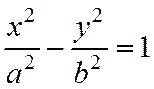
является уравнением гиперболы: оно называется каноническим уравнением гиперболы.