Решение дифференциального уравнения изогнутой оси балки
Если балка имеет постоянную толщину, то есть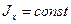 
, то решение легко записывается в общем виде:
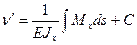(16.10)
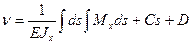(16.11)
Хотя решение получено в общем виде, однако основная трудность заключается в определении Мх иконстант C и D, поскольку на разных участках балки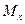 
разные, а значит C и D также разные (в частности, если балка имеет три участка, то нужно определить 6 констант C и D).
Однако существует способ интегрирования, который сводит все неизвестные только к двум константам (разработан Клебшом)
Дата добавления: 2015-08-11; просмотров: 628;