Конвективный теплообмен

Перенос в движущейся среде любой субстанции (массы, импульса, теплоты) происходит как молекулярным хаотическим движением, так и конвективным (макроскопическим) движением молей газа или жидкости. Конвективный теплообмен и трение по тракту двигателей изучают в концепции пограничного слоя, введенной Л. Прандтлем в механику жидкости и газа в 1904 г. Поток продуктов сгорания разделяют на область невязкого и нетеплопроводного ядра и пристеночную область, именно в которой происходит перенос импульса, теплоты и массы. Такой подход позволил существенно упростить задачу вычисления потоков теплоты и получить практические результаты.

Рассмотрим обтекание газовой фазой продуктов сгорания тракта некоторого условного РД с классическим соплом Лаваля согласно рис. 7.1. В общем случае можно допустить существование трех пограничных слоев: динамического, в котором происходит перенос импульса и возникают напряжения трения на стенке; теплового, в котором происходит перенос теплоты и возникает тепловой поток в стенку, и диффузионного, в котором происходит перенос компонент газовой смеси и возникает поток массы к стенке. На рис. 7.1 принята аналогия между переносом теплоты и массы (скалярная субстанция переноса, в отличие от импульса). Для пограничного слоя принята следующая система координат: продольная по контуру сопла s и нормальная к стенке 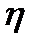ввиду того, что в теории сопла осевую координату обозначают х, а радиальную - либо r, либо у.

Математические формулировки потоков импульса, теплоты и массы получают в рамках линейной термодинамики необратимых процессов, близких к равновесию. При малых отклонениях от равновесия поток какой-либо субстанции есть произведение обобщенной термодинамической силы на коэффициент пропорциональности. Такое линейное соотношение именно и называют феноменологическим законом.

Тепловые и диффузионные потоки в смеси газов возникают при наличии хотя бы одного из следующих факторов:

- градиент температуры;

- градиент давления;

- градиент концентрации.

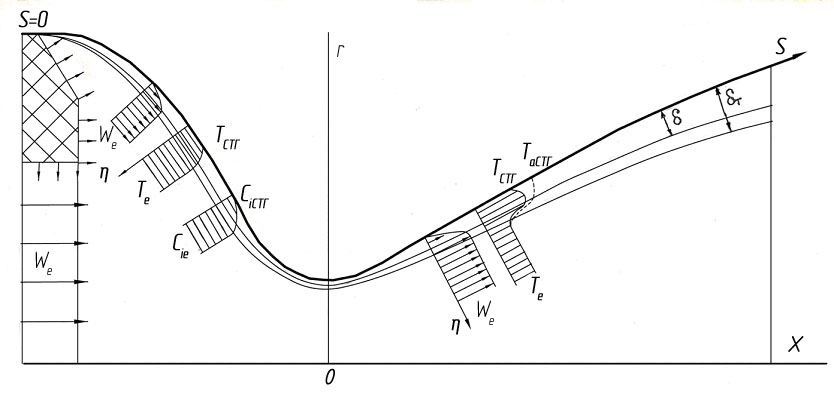
Рис.7.1. Развитее пограничных слоев по тракту сопла

Воздействие движущейся газовой фазы на стенку конструкции определяет напряжения трения, плотность конвективного теплового потока и массовую скорость подвода химически активных компонент. Значения их вычисляют с помощью феноменологических законов Ньютона, Фурье и Фика:

- напряжение трения ,

- плотность теплового потока 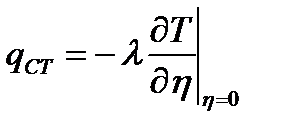, (7.1)

- плотность потока массы i-го компонента .

Здесь: 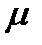- динамическая вязкость газа,

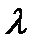- теплопроводность газа,

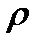- плотность газа,

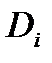- коэффициент диффузии i-гo компонента газа.

Тогда для определения напряжения трения и плотностей потоков теплоты и массы остается определить значения производных скорости, температуры и концентрации по нормальной к стенке координате на поверхности. А это оказалось исключительно трудной задачей, и механика жидкости и газа этим занимается более 100 лет.

Перенос импульса в жидкости или в газе, т.е. распределение касательных напряжений в потоке и на стенке сформулированы в уравнениях Навье-Стокса еще в середине XIX века. Но решение их во всем спектре возникающих практических задач до сих пор отсутствует, несмотря на огромную производительность имеющихся компьютеров. В первую очередь, это вызвано возникновением турбулентности.

Сначала инженеры при создании энергетических установок использовали эмпирические зависимости, полученные в экспериментах с помощью теории размерностей и подобия.

Более простым и доступным для исследования является выражение плотности конвективного теплового потока в стенку обтекаемой конструкции в виде закона Ньютона:

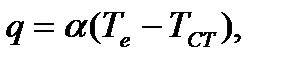(7.2)
где 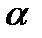- коэффициент пропорциональности или коэффициент конвективного теплообмена. Выражение (7.2) cтpoгo соответствует случаю обтекания тела несжимаемым стационарным потоком газа с постоянной во времени и по длине температурой 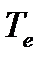и постоянной во времени и по длине тела температурой поверхности 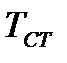- тогда можно говорить о существовании коэффициента пропорциональности между плотностью теплового потока и термодвижущей силой, т.е. разностью температур 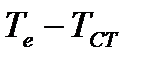. Сравнение (7.1) и (7.2) показывает, что 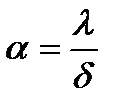, где 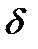- толщина пограничного слоя, но как определить эту толщину? - вся проблема в этом.

Практика создания технических устройств подтвердила применимость концепции коэффициента теплообмена не только в таких жестких условиях, но и при переменной температуре рабочего тела и температуре поверхности, а также действия ряда других факторов.

В сжимаемых течениях используют более корректный аналог формулы (7.2):

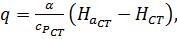
где 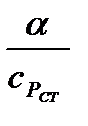- аналог коэффициента теплообмена или коэффициент массобмена (размерность 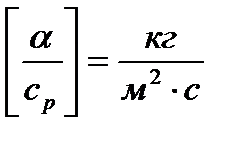), 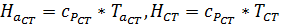- энтальпия восстановления на адиабатической поверхности и энтальпия газа при температуре стенки (изменение температуры газа поперек пограничного слоя существенное и значение удельной теплоемкости также может сильно изменяться).

Напомним основные числа и критерии подобия:

- число Рейнольдса как меру отношения инерционных и вязкостных сил в поток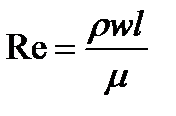е , где 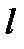- характерный размер исследуемой области течения;

- число Прандтля как отношение толщин динамического и теплового пограничных слоев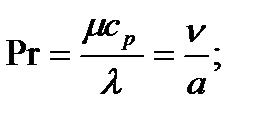

- число Нуссельта как отношение переноса теплоты конвекцией к переносу теплоты молекулярной теплопроводностью газа, ;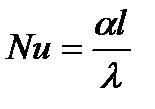

- число Стантона как отношение теплоты, подведенной к стенке обтекаемого тракта, к энергии движущегося газа ;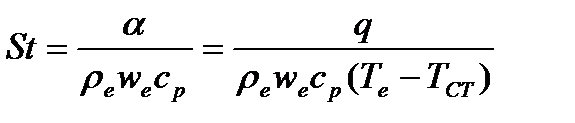

- диффузионное число Стантона как отношение массовой скорости вещества к стенке к плотности потока его в ядре ;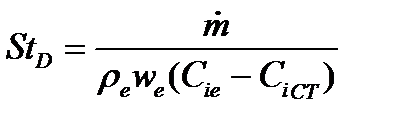

- число Шмидта как отношение переноса импульса к переносу вещества диффузией в бинарной смеси газов 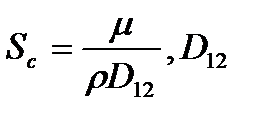- коэффициент бинарной диффузии.

Связь между числами Стантона и Нуссельта имеет вид 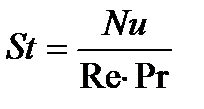, а отношение чисел Прандтля и Шмидта есть число Льюиса 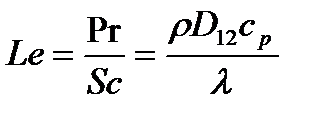(отношение интенсивностей диффузионного и кондуктивного переноса энергии).

В общем случае различают числа и критерии подобия. Согласно А. А. Гухману критерий подобия в отличие от числа есть комплекс из величин, наперед заданный по условию. В зависимости от решаемой задачи некоторые комплексы могут быть как числами, так и критериями.

Для безградиентного несжимаемого турбулентного пограничного слоя на гладкой непроницаемой пластине 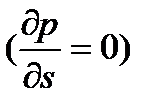коэффициенты теплообмена вычисляют из соотношения

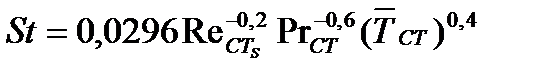, (7.3)
где 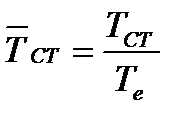- температурный фактор; индекс «ст» означает, что все величины чисел подобия вычисляются при температуре стенки, т.е. 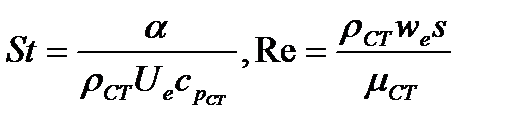, s - продольная координата расчетного сечения. Обычно пренебрегают небольшим начальным участком ламинарного режима течения.

Применяются также критериальные зависимости для стабилизированного течения жидкости в трубах 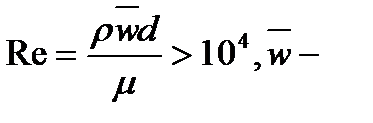средняя скорость

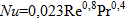, (7.4)
в которой величины в числах подобия определены при температуре жидкости, а характерным размером служит диаметр трубы d, т.е. .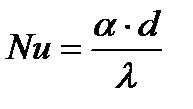

В 50-е годы XX века появилась работа Д.Р. Бартца (США) по исследованию конвективного теплообмена в соплах с небольшими значениями углов до- и сверхзвуковых частей контура на гладкой непроницаемой поверхности. Расчетная зависимость аналогична эмпирическим соотношениям для труб типа (7.4) только коэффициент согласования имел значение 0,026 для дозвуковой части и 0,023 для сверхзвуковой.

Но обтекание материалов тракта сопла даже простой конструкции (рис.7.1) уже характерно наличием ряда возмущающих факторов по сравнению с наиболее простыми (эталонными) условиями при течении на гладкой непроницаемой пластине.

К первой группе факторов относят особенности обтекания потоком продуктов сгорания:

- турбулентный режим в пограничном слое по тракту двигателя, за исключением отдельных небольших участков;

- сжимаемость (число Маха может достигать М = 4,5);

- градиент давления, особенно за минимальным сечением сопла;

- повышенная турбулентность ядра потока;

- двухфазность рабочего тела (продукты сгорания металлизированных топлив) (для РДТТ);

- сильная неизотермичность пограничного слоя;

- возможная нестационарность расхода рабочего тела.

Ко второй группе относят факторы, характеризующие состояние поверхности стенки:

- изменение температуры поверхности во времени и по длине тракта; проницаемость (вдув или отсос газа);

- шероховатость;

- тепловые эффекты окисления и испарения материалов.

Поэтому необходима реализация теории пограничного слоя с привлечением данных многочисленных экспериментов. На практике для расчетов коэффициентов теплообмена на гладкой непроницаемой, поверхности тракта сопла используют методику В.С. Авдуевского, учитывающую наличие отрицательного градиента давления, сжимаемость газа и неизотермичность пограничного слоя:

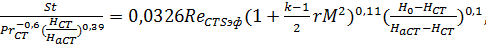(7.5)
где 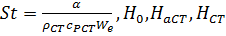- значения энтальпии потока при температуре торможения, восстановления и стенки, r - коэффициент восстановления температуры.

Число Рейнольдса определено по эффективной длине обтекаемого контура :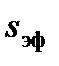

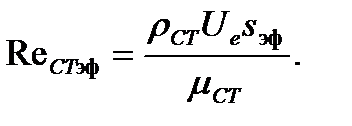
Эффективная длина пограничного слоя как раз учитывает наличие отрицательного градиента давления и определена из условия равенства интегральных характеристик пограничного слоя на пластине и в ускоренном течении.

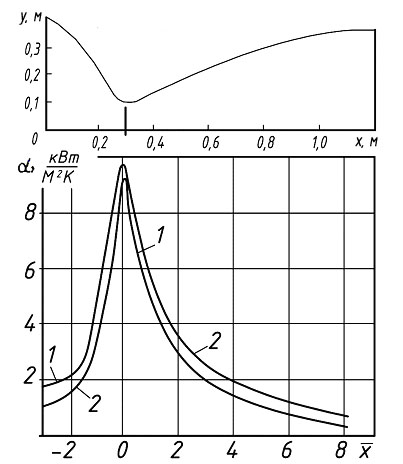
Распределение значений коэффициентов теплообмена по тракту сопла, рассчитанных по формуле Бартца и методике B.C. Авдуевского, показано на рис. 7.2.