Применение метода наложения к анализу цепей несинусоидального тока
|
R¹R(w)
|
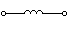
| XL(k) |
XL(k)=KwL; w=>XL
| XC(k) |
|
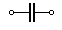
XC(k)=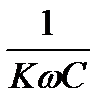 
; w=>XC¯
|
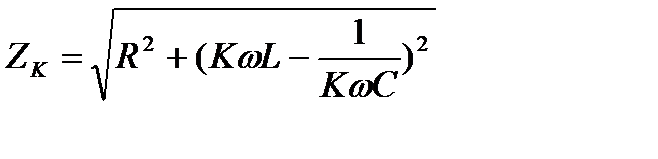
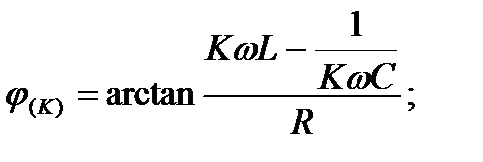
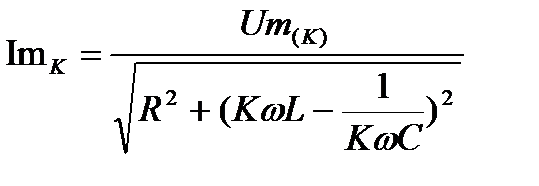
1. Представляем несинусоидальной ЭДС (или Uвх) в виде ряда Фурье. Считаем, что каждая гармоника напряжения действует независимо от других. Расчет ведем для каждой гармоники в отдельности, используя метод комплексных амплитуд (символический метод). Результирующий ток находится как сумма токов отдельных гармоник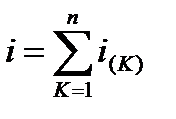 
2. Т. к. z,y=f(w), то кривая тока не повторяет кривую напряжения, и кривые напряжения на отдельных элементах (за исключением резистивных) не повторяют кривую тока.
3. Векторные диаграммы строятся для каждой гармоники в отдельности, складывать вектора разных гармоник нельзя.
Пример:
| u=180sinwt+60sin3wt+40sin(5wt+18°) R=10 Ом; L=0,05 Гн; С=22,5 мкФ; f=50 Гц |
1) Расчет для 1-й гармоники:
z 
= 
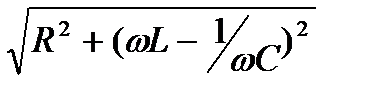=126 (Ом); j 
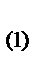=arctg 
I 
= 
i 
=1,43sin(wt+85°); (j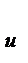=y 
-y 
)
2) Расчет 3-й гармоники:
z 
= 
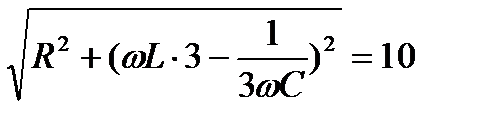(Ом); j 
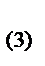=arctg 
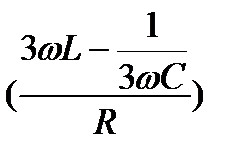=0 => резонанс напряжений на 3-й гармонике
I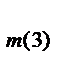 
= 
= 
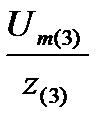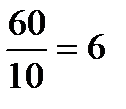(A); i 
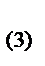=6sin3wt
3) Расчет для 5-й гармоники:
z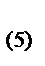 
= 
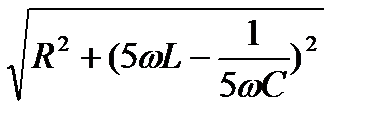= 51 (Ом); j 
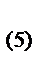=arctg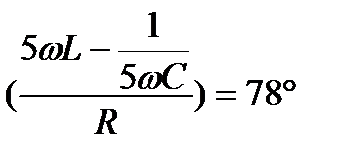 
I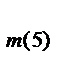 
= 
= 
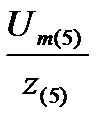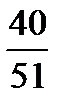=0,78 (A); i 
=0,78sin(5wt-60°)
Ответ: i=1,43sin(wt+85°)+6sin3wt+0,78sin(5wt-60°), A
Дата добавления: 2015-08-11; просмотров: 1439;