Свойства ортогонального проецирования.

а) Позиционные свойства (Рис.4):

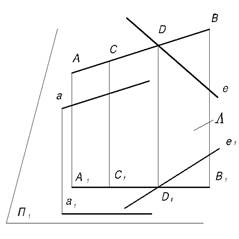1. каждой точке проецируемого Г.О. соответствует одна точка на плоскости проекций,

А Þ А1;

(обратная зависимость неоднозначна);

2. проекцией прямой линии АВ является прямая линия А1В1,

АВÞА1В1; АВА1В1– проецирующая плоскость L);

3. если точка принадлежит линии, то ее проекция принадлежит проекции данной линии,

С Ì АВ Þ С1 Ì А1В1;

Рис.4 4. проекцией точки пересечения двух прямых является точка пересечения проекций данных прямых;

D = АВхеÞ D1 = А1 В1хe1;

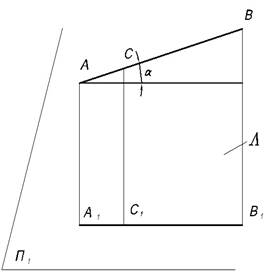
Б) метрические свойства (Рис.5)

1. При ортогональном проецировании величины отрезка прямой (АВ) и его проекции (А1В1) связаны между собой соотношением

А1В1= АВ * Соs ; ,

где ; - угол наклона прямой АВ к плоскости проекций П1.

Примечания:

а) если ; = 0 , то АВ = А1В1;

б) если ; = 90 , тоА1В1= 0.

Рис.5

Плоскость L(АВА1В1) называется проецирующей плоскостью (L^П1).

2. При ортогональном проецировании отношения между отрезками прямой пропорциональны соответствующим отношениям между их проекциями.

АС:СВ = А1С1: C1B1

АС : AB = А1С1: A1B1 и т.д.