строка: II излом
1 столбец: rт1/ rт’2
(знач.ст.1, 4 стр./след. по возраст)
4 столбец: предыдущая нагрузка
6 столбец:
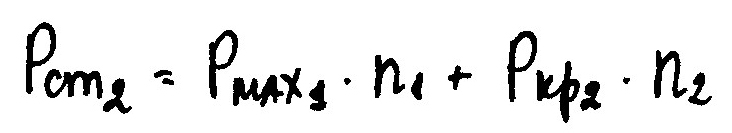
7 столбец:
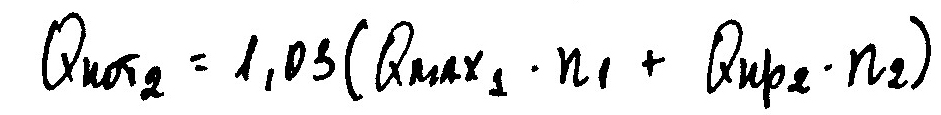
8 столбец: по Qкот2 находим rк2
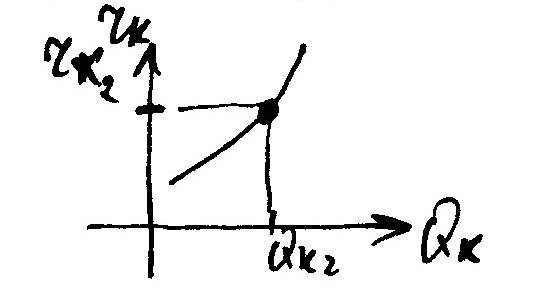
9 столбец:

Строка
7 столбец: Qmaxкот
Строка
1 столбец: rт’2
2,3 столбцы: Qmax1,Pmax1
7 столбец:
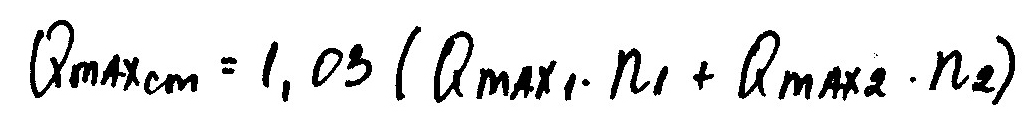
8 столбец:
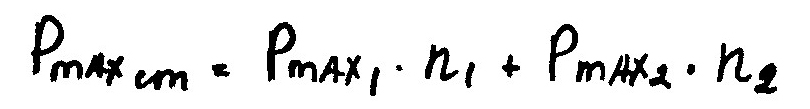
Строка
Сравнение Qmaxк и Qmaxст
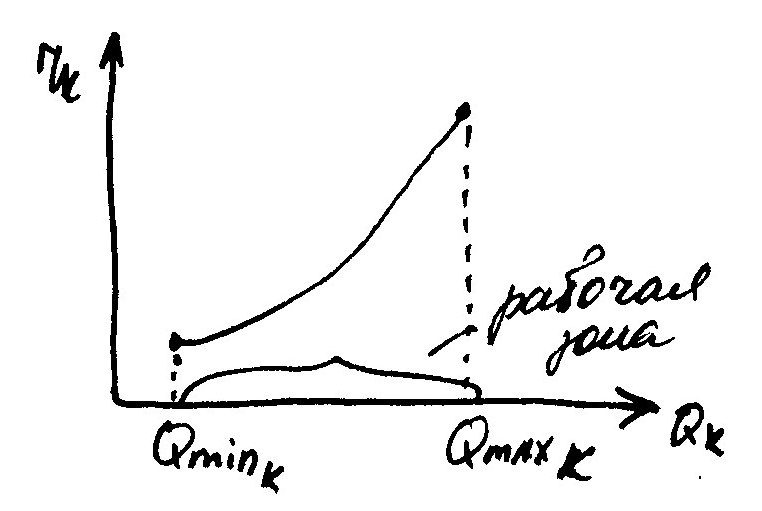
1) Qmaxст<Qmaxк
Значения 8 строки->в 9 строку
2)Qmaxст>Qmaxк
7 столбец: min значение Qmaxк
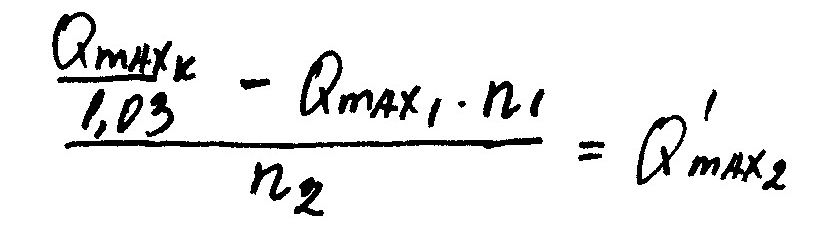
5 столбец:
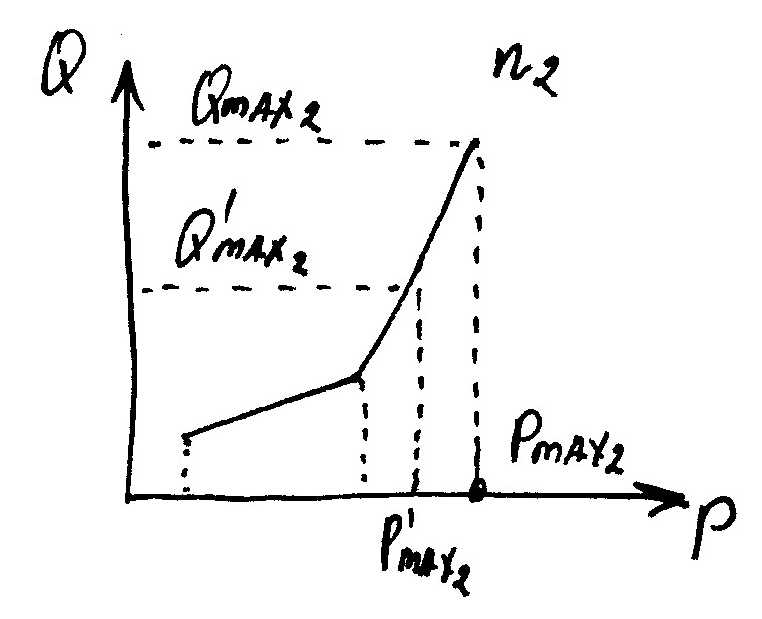
6 столбец:
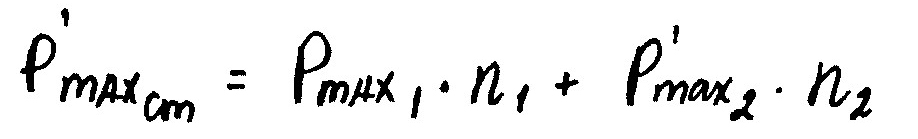
8 столбец: rк3
9 столбец:

По результатам таблицы строим:
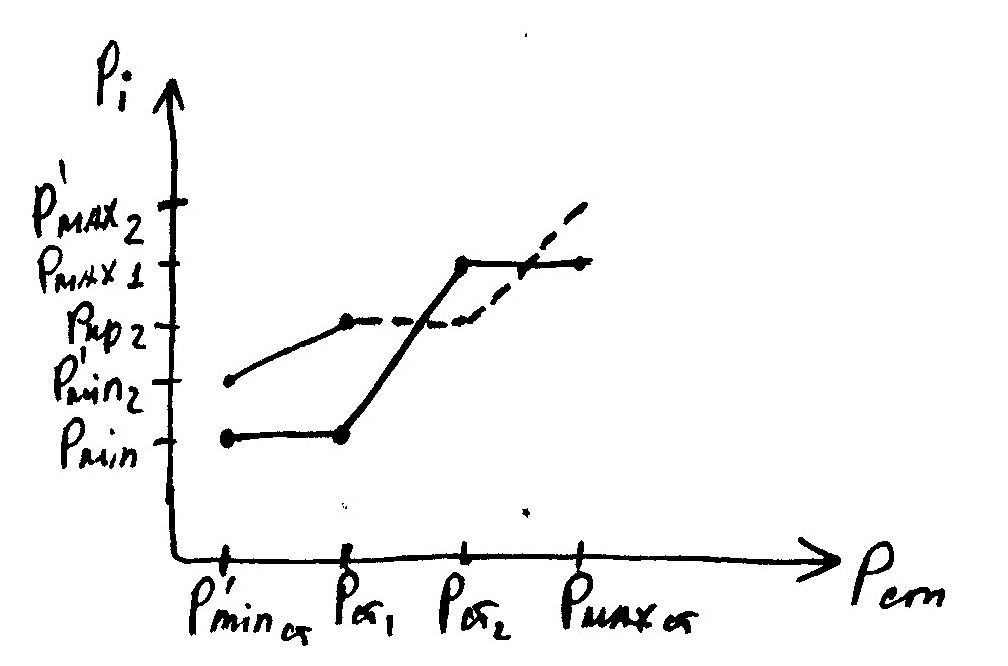
1) ХОПст (9 и 6 столбцы)
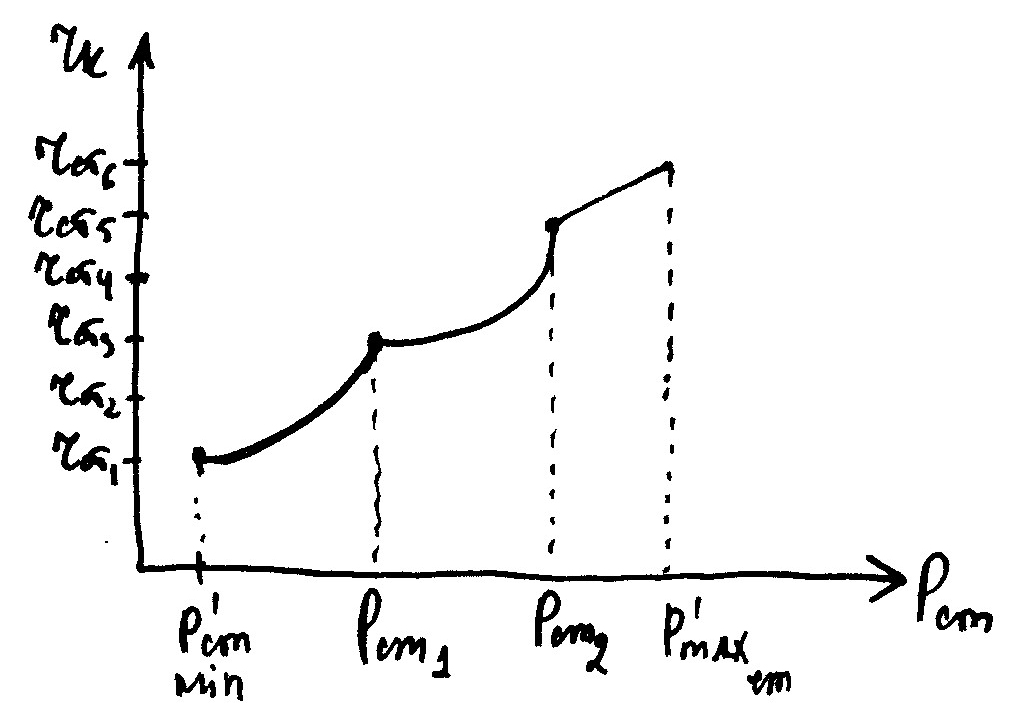
2) Режимная карта машинного зала
Лекция 14
Вывод условия оптимального распределения нагрузки в энергосистеме.
Система состоит из тепловых станций.
Целевая функция:
1) Bà min
2) Характеристики объектов:
к.а: B=f(Q)
т.а.: Q=f(P)
3) Ограничения:
а)неравенства:
Qminк ≤ Qк ≤Qmaxк
Pmini ≤ Pi ≤ Pmaxi
б)равенство: баланс мощности системы
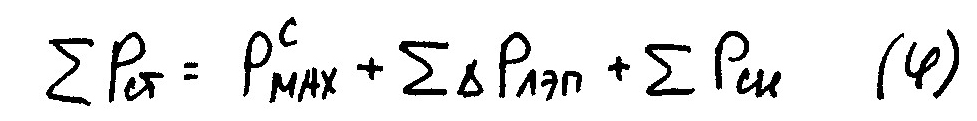
4)Уравнение управления:
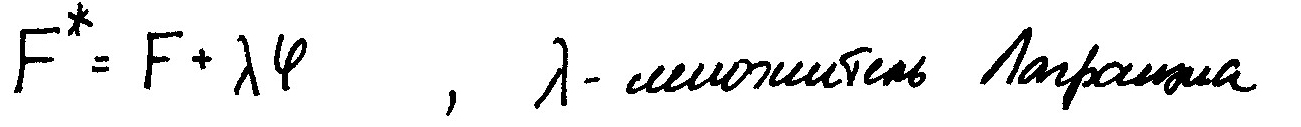
Решаем уравнение управления:
1. Дифференцируем уравнение управления по переменной нагрузки каждой станции, и первую производную приравниваем к нулю.
В результате получаем следующую систему уравнений:
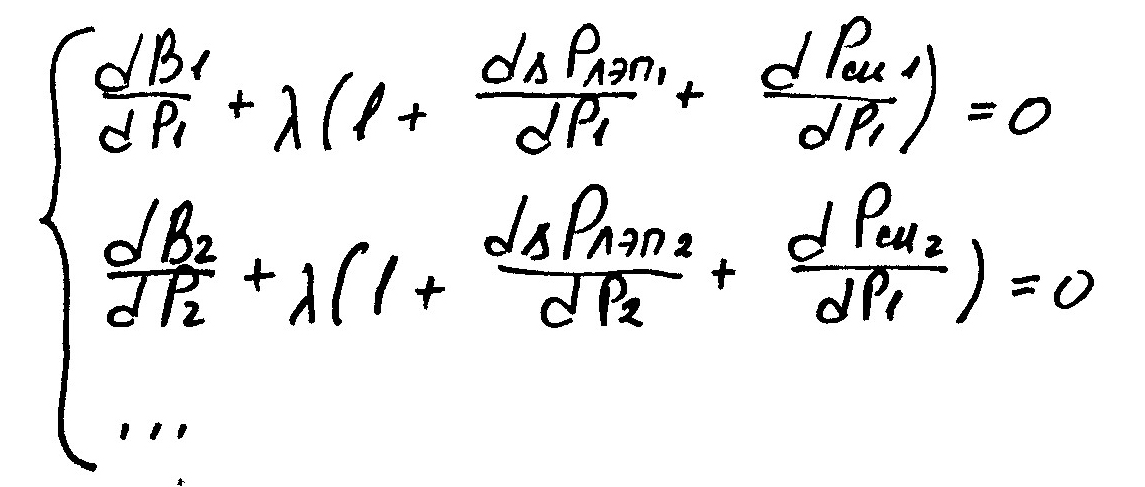
Количество уравнений соответствует количеству станций.
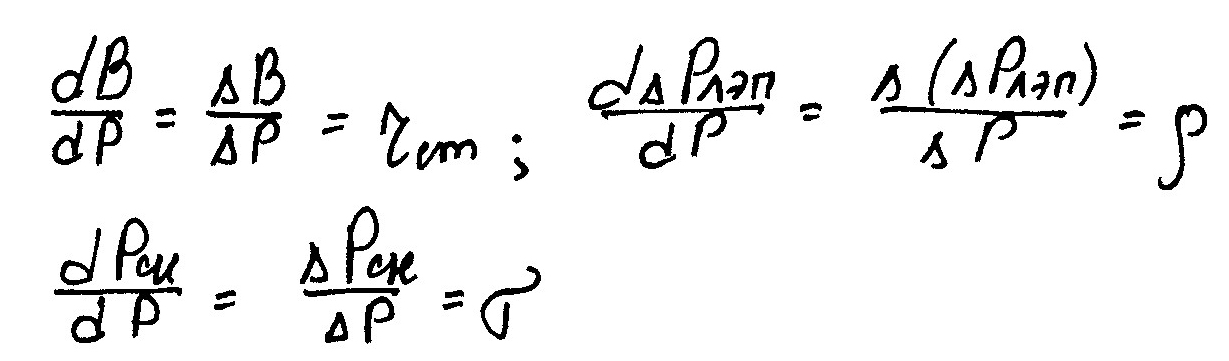
Относительный прирост изменения потерь (ρ) – характеризует на сколько меняется потери в ЛЭП при изменении нагрузки станции на 1 МВт.
Численные показатели ρ и σ малы. Они получены путем непосредственного дифференцирования потерь в ЛЭП и собственных нужд станции.
(σ) – отражает на сколько меняется собственные нужды станции при изменении нагрузки на 1 МВт.
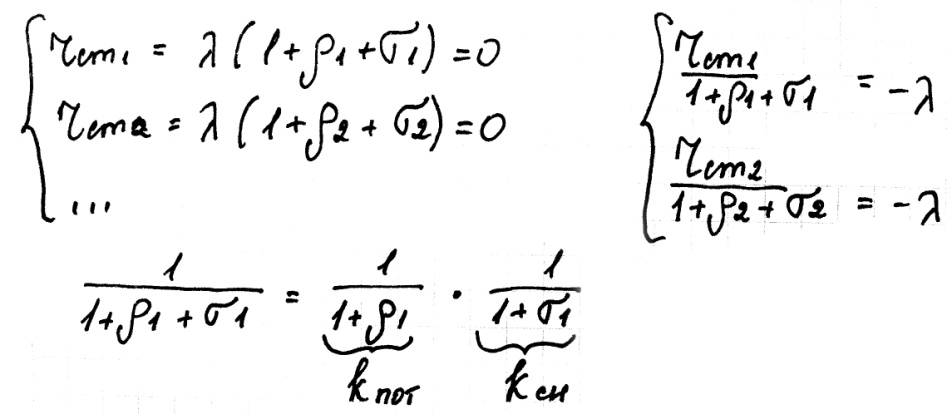
Условия оптимального распределения нагрузки:
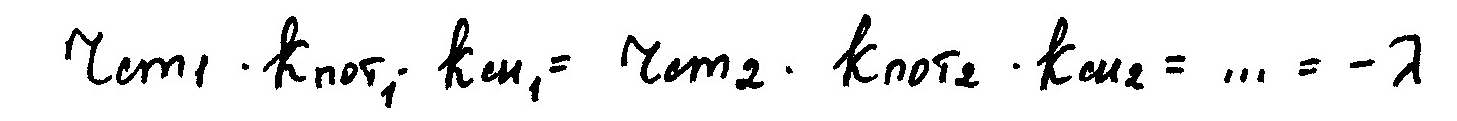
Осуществляя распределение нагрузки с соблюдением равенств относительных приростов между станциями системы, мы получаем такую нагрузку каждой станции, что в расход топлива в системе будет минимальный.
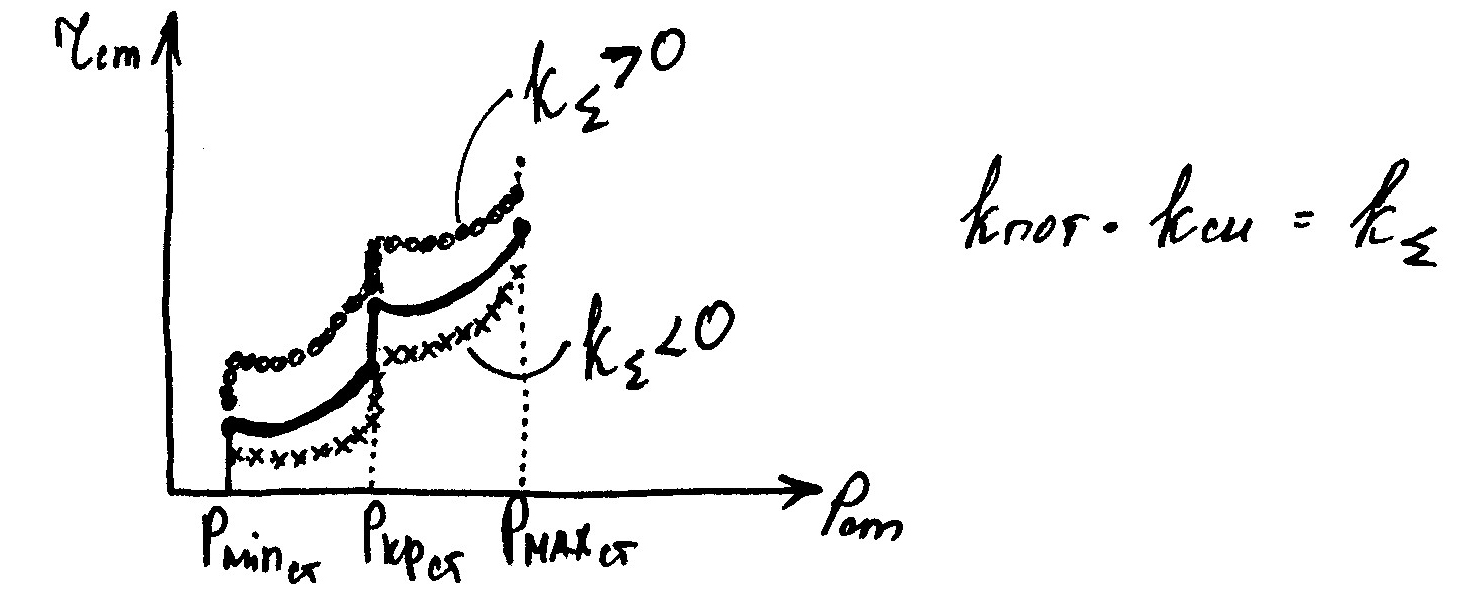
Если суммарный коэффициент больше единицы, характеристика параллельно самой себе поднимается. Если меньше единицы, характеристика опускается. Та станция которая имеет суммарный коэффициент меньше единицы и характеристика опускается достаточно низко, то станция дополнительно нагружается. Та станция, которая имеет суммарный коэффициент больше единицы, станция разгружается.
Если в качестве критерия - минимум денежных затрат, то условия оптимального распределения нагрузки:
Целевая функция:
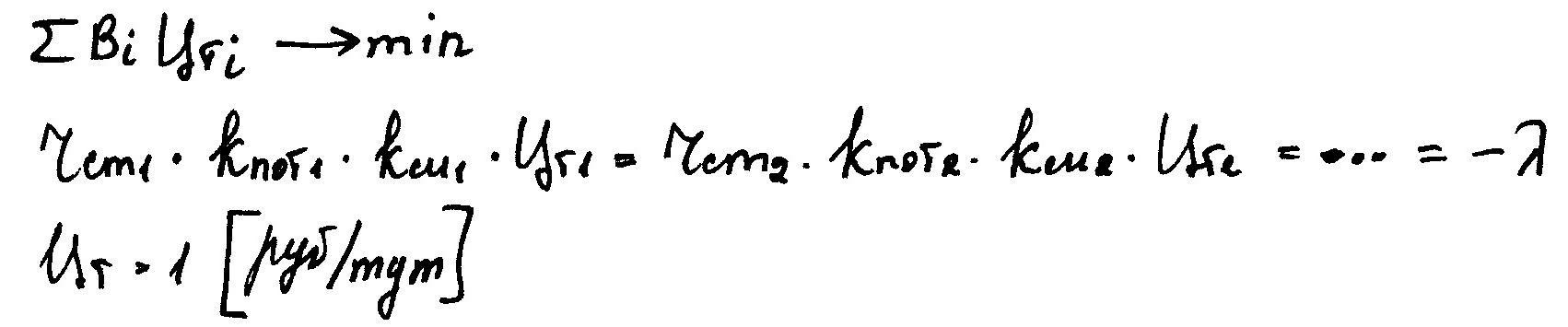
Атомные станции после Чернобыльской аварии имеют базовый режим работы. А ГЭС, имеющие большой объем водохранилища (регулируют сток в течении всего сезона или нескольких лет), участвуют в оптимизации режима.

Изломы связаны с последующим включением агрегата.
Показатель относительного прироста:
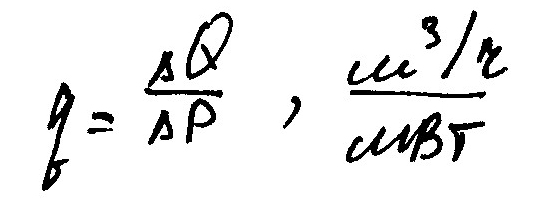
Характеризует сколько дополнительно воды необходимо пропустить в спиральную камеру, что бы увеличить нагрузку турбины на 1 МВт.
3.Неравенства:
Qminк ≤ Qк ≤Qmaxк
Pmini ≤ Pi ≤ Pmaxi
Pmin ≤ Pгэс ≤ Pmax
Равенства:
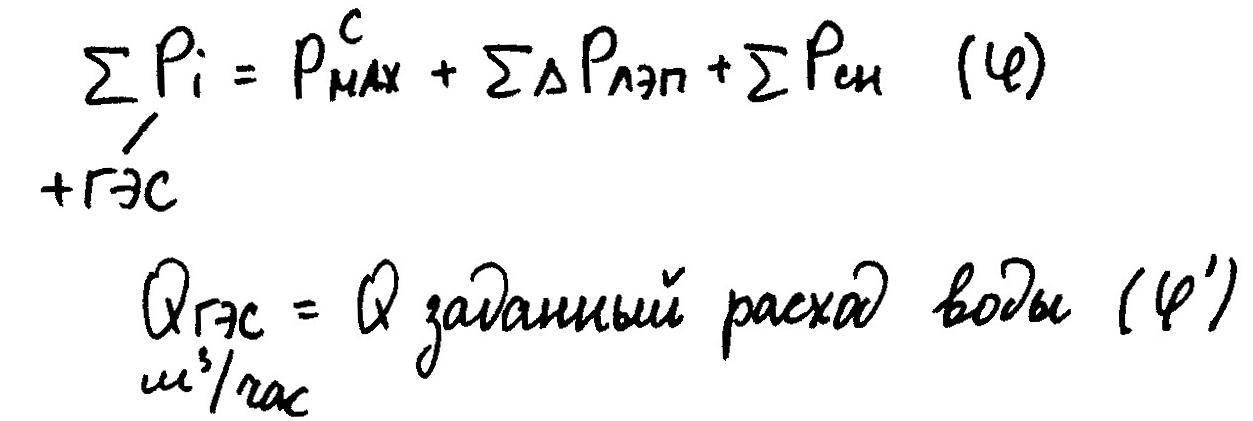
Заданный расход воды связан с графиком сработки водохранилища.
Уравнение управления:

Решаем уравнение путем дифференцирования уравнения управления по переменной нагрузки каждой станции и приравнивая первую производную к нулю. Получаем следующее условия оптимального распределения нагрузки:
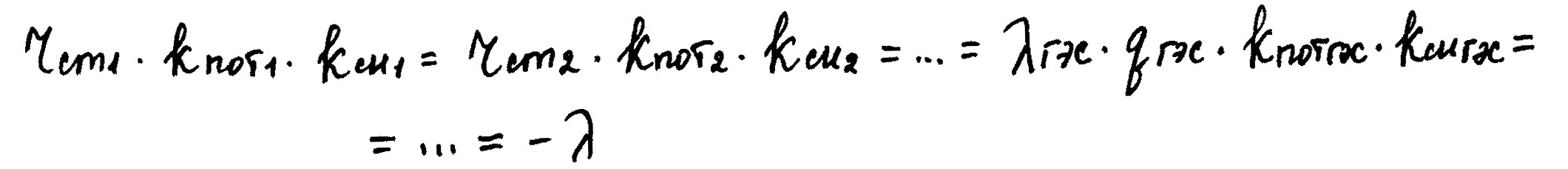
Экономический смысл λгэс - показателя топливной эффективности ГЭС- отражает, сколько топливо мы экономим на тепловых станциях системы, если расход воды увеличим на 1 метр кубический в час.
Построение ХОП-системы.
Будем строить с учетом равенства относительных приростов между станциями системы.
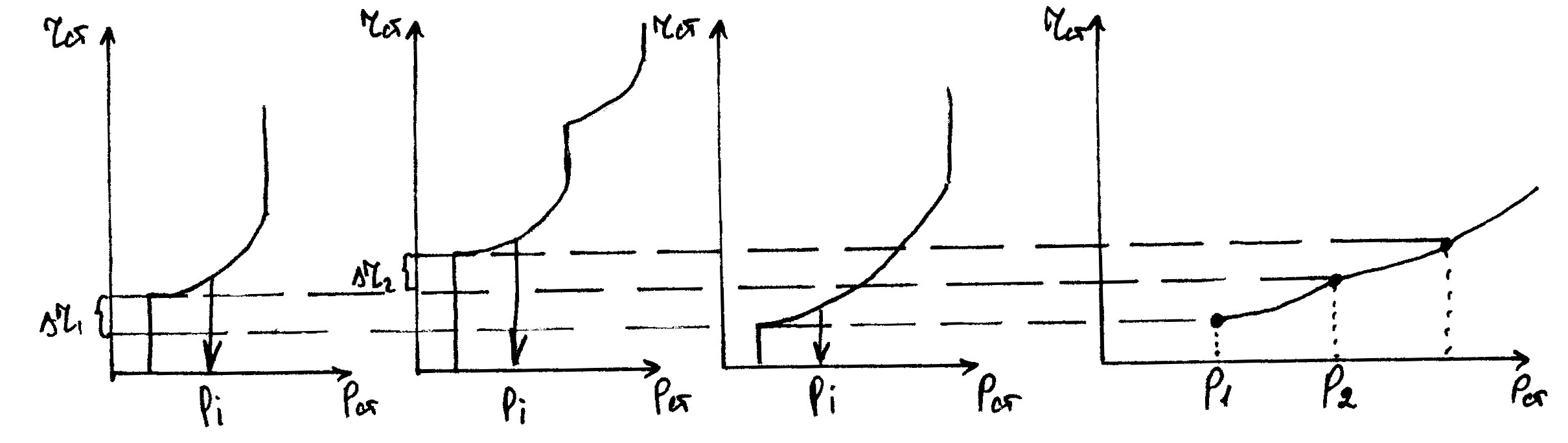
r1: Pсист1 = Pmin1+Pmin2+Pmin3
r2: Pсист2 = Pmin1+Pmin2+P3
r3: Pсист3 = Pmax1+Pmin2+P4
ХОП-система необходима для определения нагрузки каждой станции, зная нагрузку системы.
Нагрузка системы задана графиком нагрузки:
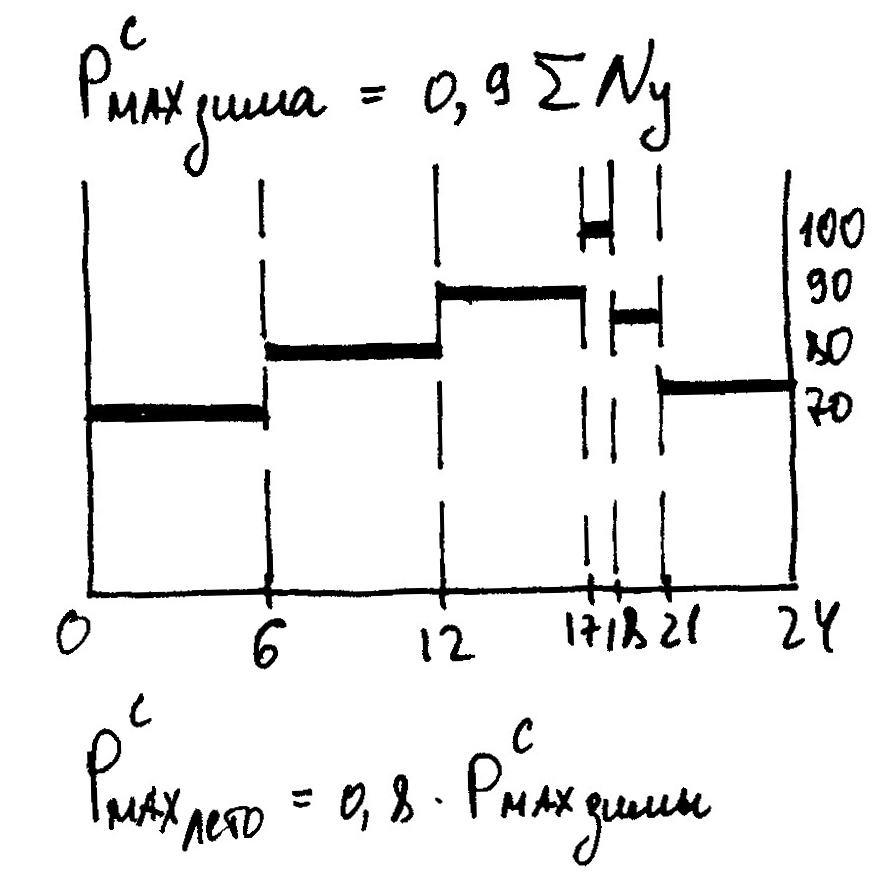
| Часы суток | Pсуточ, МВт | P1 | P2 | P3 | |
| 0-6 | |||||
| 6-12 | Pi | √ | √ | √ |
Итоговые показатели:
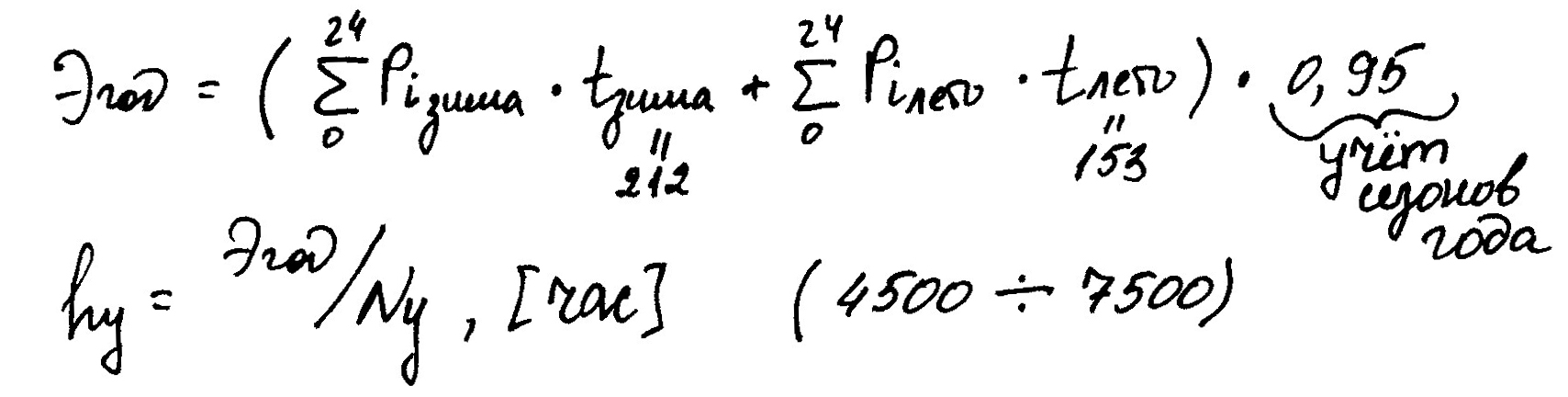
Дата добавления: 2015-08-11; просмотров: 678;
