Учебный вопрос № 1. Сущность процесса дросселирования
Дросселированием называют необратимый процесс, в котором давление при прохождении газа через ссуженное отверстие уменьшается без совершения внешней работы.
Всякое сопротивление в трубопроводе (вентили, задвижка, шайба кран, клапан и др.) вызывает дросселирование газа и, следовательно, падение давления.
Величина падения давления зависит от природы рабочего тела, его состояния, величины сужения газопровода и скорости движения газа.
В большинстве случаев дросселирование, сопровождающееся уменьшением работоспособности тела, приносит безусловный вред, Но иногда оно является необходимым и создается искусственно, например, при регулировании паровых двигателей, в холодильных установках, в приборах, замеряющих расход газа и т.д.
Газ при прохождении через отверстие, представляющее известное сопротивление, кинетическая энергия газа и его скорость в узком сечении возрастают, что сопровождается падением температуры и давления (рис. 1).
Примером процесса дросселирования является выпуск сжатого газа из баллона. Температура газа на выходе из баллона резко понижается и вентиль обмерзает.
Процесс дросселированияподчиняется обшей теория газового потока,
| Р1, V1, Т1 Сжатый газ |
| Р2, V2, Т2 Расширенный газ |
| Рис. 1. Принципиальная схема дросселирования. |
основные положения которого были изложены Д.Бернулли, Н.Е.Жуковским и Чаплыгиным. Особое значение имеют работы Жуковского "Истечение газа под большим напором" и "О трении газов".
Большинство реальных газов (воздух, кислород, азот, углекислота и др.) при дросселировании в обычных условиях понижают свою температуру.
В основе этого процесса лежит эффект охлаждения, обнаруженный Джоулем и Томсоном в 1852 г. при адиабатномдросселировании реального газа. Этот процесс протекает как без теплообмена» так и без совершения полезной внешней работы.
Эти ученые произвели опыт с пропусканием сжатого газа через пористую пробку, вставленную в трубку, и установили, что при расширении газа во время прохождения через пробку происходит охлаждение его.
Дросселирование протекавшего газа или жидкости возникает в том случае, когда поток внезапно сужается вследствие уменьшения сечения, а затем опять получает возможность двигаться в большем сечении.
В ссуженном сечении скорость потока возрастает, что одновременно вызывает понижение температуры потока и, следовательно, уменьшение его внутренней энергии.
Кинетическая энергия, полученная потоком в процессе дросселирования, расходуется на трение, превращается в тепло, которое воспринимается самим потоком. Этот процесс приводит к изменению внутренней энергии и температуры дросселируемого вещества, а в случае дросселирования влажного пара - и к увеличению его сухости. В зависимости от свойств и состояния дросселируемого вещества внутренняя энергия за дроссельным участком может быть больше или меньше, либо равной внутренней энергии до дроссельного участка. От этого соотношения зависит изменение состояния дросселируемого вещества, следовательно, конечная температура вещества может быть выше, равна или ниже начальной.
Подвод тепла за счет внутреннего трения приводит к изменению не только внутренней энергии, но и к возрастанию энтропии дросселируемого вещества, которая увеличивается не за счет внешних теплопритоков, а вследствие сообщения потоку тепла, эквивалентного потерянной на трение работе (энергии) самого потока, поэтому процесс дросселирования - внутренне необратимый.
Процесс дросселирования можно рассмотреть с помощью схемы, изображенной на рисунке 2.
При прохождении газа через отверстие, представляющее известное сопротивление, кинетическая энергия газа и его скорость в узком сечении возрастают, что сопровождается падением температуры и давления.
| Рис. 2. Схема процесса дросселирования |
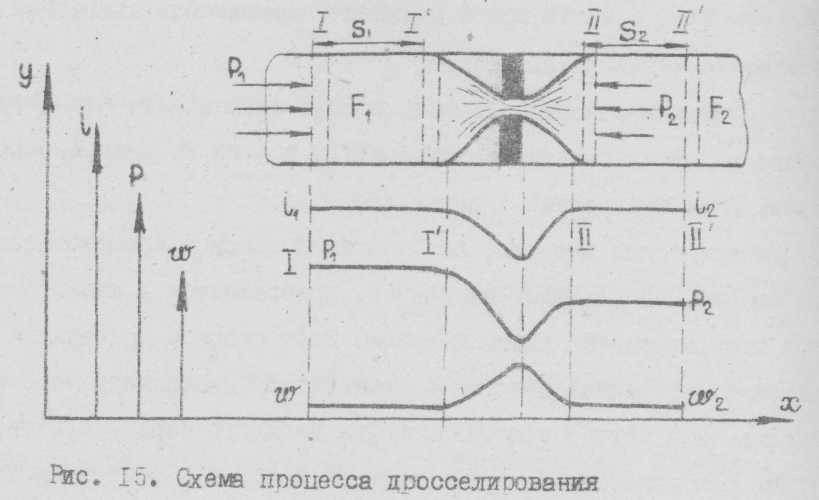
Газ, протекая через отверстие, приходит в вихревое движение. Часть кинетической энергии затрачивается на образование этих вихрей и превращается в теплоту, кроме этого, как было указано выше, в теплоту превращается и работа, затраченная на преодоление сопротивлений (трения).
Вся эта теплота воспринимается газом, в результате чего температура его изменяется и может как уменьшаться, так и увеличиваться.
В отверстии скорость газа увеличивается. За отверстием, когда газ течет по полному сечению, скорость его вновь понижается, а давление увеличивается, но до начального значения оно не поднимается; некоторое изменение скорости произойдет в связи с увеличением удельного объема газа от уменьшения давлении.
Дросселирование, как указывалось выше, является необратимым процессом, при котором всегда происходит увеличение энтропии и уменьшение работоспособности рабочего тела.
При перемещении I кг газа через отверстие поршень I переместятся в положение I', а поршень II в положение 11' , при этом поршень I совершит путь S1 , а поршень II – путь S2.
Для перемещения I кг газа необходимо затратить работу P1S1F1 или P1Q1.
Часть этой работы P2S2F2 или P2V2 будет израсходована на преодоление давления P2, а разность работ P1V1–P2V2 вызовет изменение энергии рабочего тела.
| w22– w12 |
| w12 |
| w22 |
| = 0, |
| – |
отсюда
(U1 – P1V1) – (U2 – P2V2) = 0
i1 – i2 = 0 i1 = i2
Полученное равенство показывает, что энтальпия в результате процесса дросселирования не изменяется. Этот вывод к промежуточным состояниям газа неприменим.
Энтальпия идеального газа является однозначной функцией температуры. Отсюда следует, что в результате дросселирования идеального газа температура его не изменяется Т1 = Т2.
В результате процесса дросселирования реального газа энтальпия для начальных и конечных давлений остается одинаковой, энтропия и объем увеличиваются, давление падает, а температуре может увеличиваться, уменьшаться или же, в частном случае, остаться без изменений.
Изученное ранее уравнение состояния Клапейрона PV = RT справедливо только для идеальных газов, которые в природе не существуют. Объем реальных газов, особенно в условиях высокого давления и низкой температуры, уменьшается при сжатии больше или меньше, чем это следует из уравнения состояния.
Уравнение Клапейрона для 1 кг реального газа имеет следующий вид: РV=ZRT,
где Z - коэффициент сжимаемости.
Сущность явления сжимаемости заключается в следующем.
Между молекулами реального газа существуют силы сцепления и отталкивания. При сжатии газа до давлений 10-20 МПа силы сцепления возрастают в большей степени, нежели силы отталкивания. За счет этих повышенных сил сцепления объем газа при сжатии уменьшается в большей степени, чем это следует по закону Бойля-Мариотта, на величину "самосжимаемости".
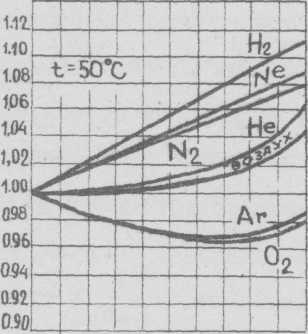
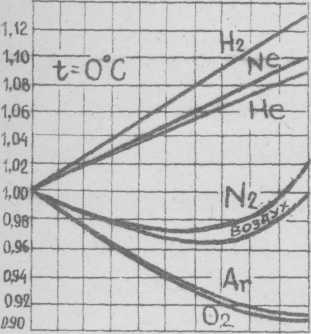
Зная коэффициент сжимаемости данного реального газа, можно по уравнению Клайперона для идеального газа определить изменение давления или объема реального газа. Кривые, по которым можно определить коэффициенты сжимаемости для некоторых газов при разных абсолютных давлениях и температурах (0 и 50°С) приведены на рисунке.
Если коэффициент сжимаемости при данной температуре и давлении меньше единицы, такой газ сжимается в большей степени, чем идеальный газ; наоборот, если z >1, газ сжимается в меньшей степени, чем это следует из уравнения Клапейрона. Для идеального газа коэффициент сжимаемости z =1.
В момент дросселирования газа давление понижается и газ расширяется. Температура идеального газа остается постоянной, но для всех реальных газов при дросселировании температура изменяется. Данное явление обусловлено присущей реальным газам большей или меньшей степени сжимаемости по сравнению с идеальным газом.
0 40 80 120 160 200 0 40 80 120 160 200
Абсолютное давление, кгс/см2 Абсолютное давление, кгс/см2
Рис. 3. Коэффициент сжимаемости реальных газов при разных абсолютных давлениях и температурах
Оно было установлено английскими учеными Джоулем и Томсоном (Кельвином).
При дросселировании реальный газ совершает два вида работы – внешнюю и внутреннюю.
Внешняя работа заключается в перемещении некоторого объема газа при том давлении, которое действует после дросселя, а внутренняя – в преодолении сил взаимного притяжения между молекулами газа в процессе его расширения. Внешняя работа может быть как положительной, так и отрицательной. Если реальный газ сжимается сильнее, чем это следует по уравнению Клапейрона, то внешняя работа будет положительной. Она производится за счет части внутренней энергии газа, вследствие чего его температура понижается, т.е. газ охлаждается.
Когда реальный газ сжимается в меньшей степени, чем следует по уравнению Клапейрона, то внешняя работа отрицательна. В этом случае используется часть работы компрессора, и газ после дросселя нагревается, так как эта избыточная работа идет на увеличение внутренней энергии газа. Внутренняя работа, производимая газом при дросселирования, всегда положительна, т.е. вызывает охлаждение газа.
Общий эффект дросселирования для каждого реального газа определяется соотношением внешней и внутренней работы и зависит от начальных условий дросселирования (начального давления и температуры газа), а также физической природы газа.
Внешняя работа для воздуха, кислорода, азота в областях давлений и температур, обычных при их дросселировании в установках глубокого холода, положительна и по своей абсолютной величине незначительна по сравнению с внутренней работой. Поэтому эти газы при дросселировании всегда охлаждаются.
Однако существуют условия, когда эти газы при дросселировании могут не охлаждаться, а наоборот нагреваться. Например, Фогель установил, что при начальной температуре 28З°Кпроцессыдросселирования воздуха с давлением выше 36,8 МПа и кислорода с давлением свыше 31,1 МПа сопровождаются нагреванием этих газов.
Учебный вопрос № 2. Эффекты дросселирования
В термодинамике низких температур различают дифференциальный, интегральный и охлаждающий эффекты Джоуля-Томсона.
Дифференциальный эффект
Дифференциальный эффект (αi) - отношение бесконечно малого изменения температуры дросселируемого газа к бесконечно малому уменьшению давления, вызывающему это изменение температуры.
Теплосодержание газа в процессе дросселирования остается постоянным (i = сonst). Уменьшение теплосодержания газа происходит всегда до начала дросселирования, т.е. в процессе сжатия газа в компрессоре до начального давления перед дросселем. При этом затрачиваемая на сжатие механическая работа переходит в тепло сжатия, которое отводится от газа водой в холодильнике. Расширившийся затем в дросселе газ будет иметь вследствие этого меньшее теплосодержание и его температура после расширения будет ниже начальной на величину интегрального эффекта. Дифференциальный эффект αi = δТ/δР.
Принимая αР = 0,1 МПа, получим αi равной изменению температуры при дросселировании, приходящейся на 0,1 МПа падения давления.
Если αi > 0, то эффект положительный;
αi < 0 – эффект отрицательный;
αi = 0 – инверсионная точка.
Величину дифференциального эффекта Джоуля-Томсона можно приближенно определить по формуле Ноэля
| Т |
где Т – начальная температура в °К;
Р – начальное абсолютное давление дросселирования;
а – коэффициент пропорциональности, учитывающий влияние сил между молекулами. Данный коэффициент имеет для каждого газа определенное числовое значение, не зависящее от паров состояния. Для воздуха а = 0,268, для кислорода а = 0,313;
в – коэффициент пропорциональности, учитывающий объем молекул или наименьший объем, до которого можно сжать газ. Величина в является учетверенным собственным объемом молекул газа. Данный коэффициент имеет для каждого газа определенное числовое значение, не зависящее от параметров состояния. Для воздуха в = 0,00086, для кислорода в = 0,00085.
Из формулы следует, что с увеличением начального давления величина αi будет уменьшаться и при а = вР станет равной нулю, т.е. температура воздуха при дросселировании понижаться не будет. Дальнейшее увеличение давления приводит к тому, что величина эффекта Джоуля-Томсона становится отрицательной и газ при дросселировании будет нагреваться.
Эта переходная точка, где меняется значение дифференциального эффекта на отрицательное, т.е. αi =0 называется точкой инверсии.
Гаузеном установлено, что величина дифференциального эффекта Джоуля-Томсона зависит от изменения температуре. Опыты Гаузена показали также, что воздух в области низких температур и давлений имеет вторую точку инверсии.
Поэтому величину дифференциального эффекта Джоуля-Томсона при расчетах находят по специальной диаграмме (рис. 4).
Сплошные линии на диаграмме соответствуют кривым постоянного абсолютного давления (изобары). Кривая насыщения показана слева пунктиром с точкой. Верхняя ее часть от критической точки относится к сухому насыщенному пару, а нижняя - к жидкости.
Вертикальная линия, проходящая через критическую точку, является критической изотермой, соответствующей Ткр = 132,6 К. Влево от нее и ниже нижней кривой насыщения воздух находится в жидком состоянии. В области давлений меньше критического эффект Джоуля-Томсона с понижением
| αi,, град на 1 кгс/см2 |
| Рис. 4. Значения дифференциального эффекта Джоуля-Томсона для воздуха при различных температурах и абсолютных давлениях |
| Температура Т, ˚К |
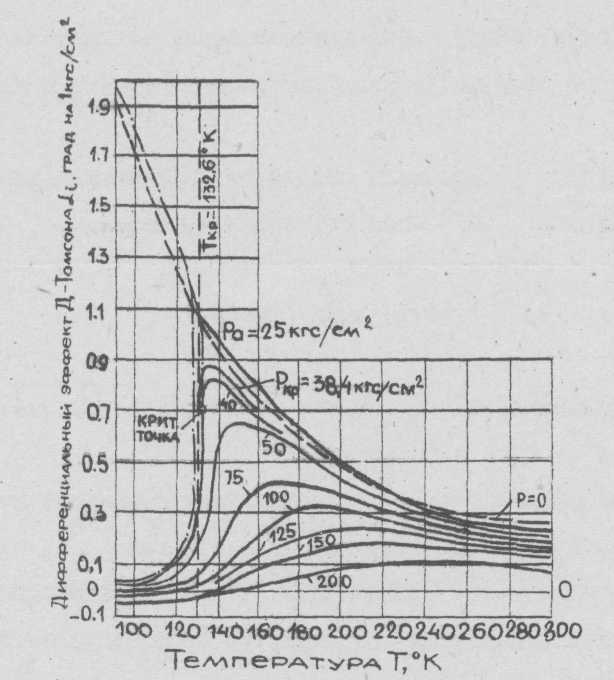

температуры увеличивается до линии насыщения. При давлениях выше критического этот эффект с понижением температуры сначала возрастает до максимума, а затем уменьшается, и тем более резко, чем ближе давление к критическому.
Дифференциальный эффект Джоуля-Томсона при высоких давлениях и низких температурах отрицательный. Точки пересечения изобар с горизонталью 0-0 являются инверсионными, так как в них αi = 0. Как видно из диаграммы изобары в правой части также где-то пересекаются с горизонталью 0-0; это соответствует вторым инверсионным точкам для воздуха в области очень высоких температур. Между двумя инверсионными точками значение дифференциального эффекта Джоуля-Томсона для воздуха всегда положительно.
Практически для приближенных подсчетов дифференциальный эффект считают равным ¼ °С при понижении давления на 1 ат.
Интегральный эффект
Эффект, наблюдающийся при больших изменениях давления, называется интегральным.
Интегральный эффект Δ Тi показывает суммарное изменение температуры при данном конечном перепаде давлений.
Величину интегрального эффекта Джоуля-Томсона вычисляют для различных начальных давлений и температур дросселирования. Кроме того величина Δ Тi может быть определена:
- непосредственным измерением температур газа в начале и конце процесса как разность Δ Тi = Т2 – Т1;
- по формуле
Δ Тi = di (Р1 – Р2)(273/Т1)2,
где: (Р1–Р2) – перепад давлений;
273/Т1 – температурная поправка с учетом начальной температуры ;
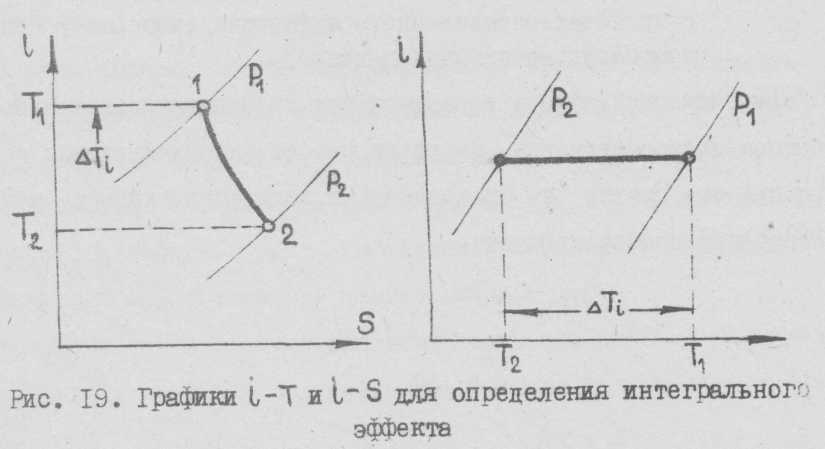
по диаграммам i – Т; i – S и др.
| Рис. 5. Графики i – Т иi – S для определения интегрального эффекта |
Изотермический (охлаждающий) эффект
Изотермический эффект ΔIт показывает количество холода в кдж, расширившегося в дросселе с начального до конечного давления.
Для расчета процессов глубокого охлаждения исключительно важное значение имеет выражение джоуль-томсоновского эффекта в кдж или так называемый изотермический эффект дросселирования, представляющий собой разность теплосодержания сжатого состояние до дросселирования и расширенного газа при одной и той же температуре начала дросселирования.
ΔIт – это величина, численно равная разности энтальпий, полученных в процессах, предшествовавших дросселированию, т.е. в результате изотермического сжатия в компрессорной установке. Между изотермическим эффектом и интегральным существует следующая зависимость
ΔIт = Ср ΔТi,
где Ср - средняя теплоемкость газа при постоянном давлении в пределах определенного интервала температур при дросселировании кдж/кг · град.
Изотермический эффект характеризует холодопроизводительность процесса дросселирования. Он равен работе межмолекулярных сил газа при его сжатии и, следовательно, количеству холода, полученному при дросселировании:
Qдр = ΔIт
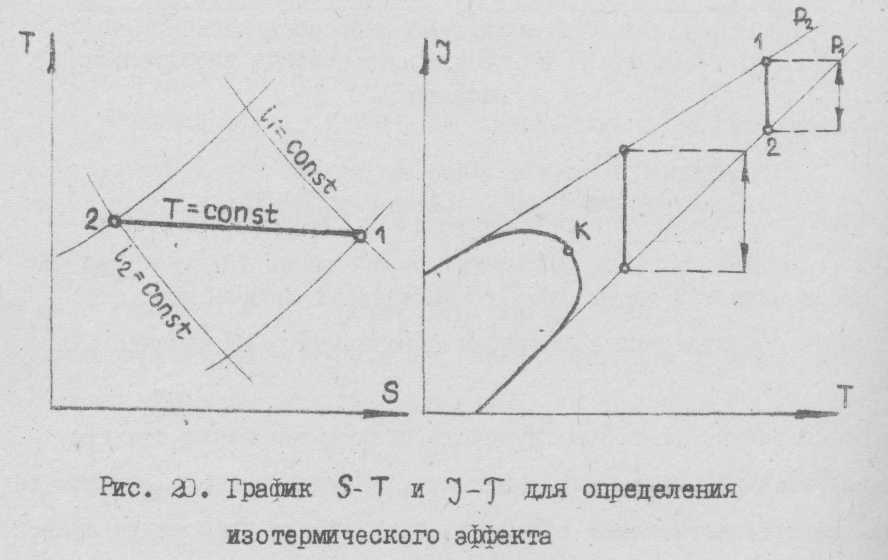
| Рис. 6. График S – Т и I – Т для определения изотермического эффекта |
Дата добавления: 2015-08-11; просмотров: 2076;
