Системы координат употребляемые в высшей геодезии.
1. Система пространственных прямоугольных координат:
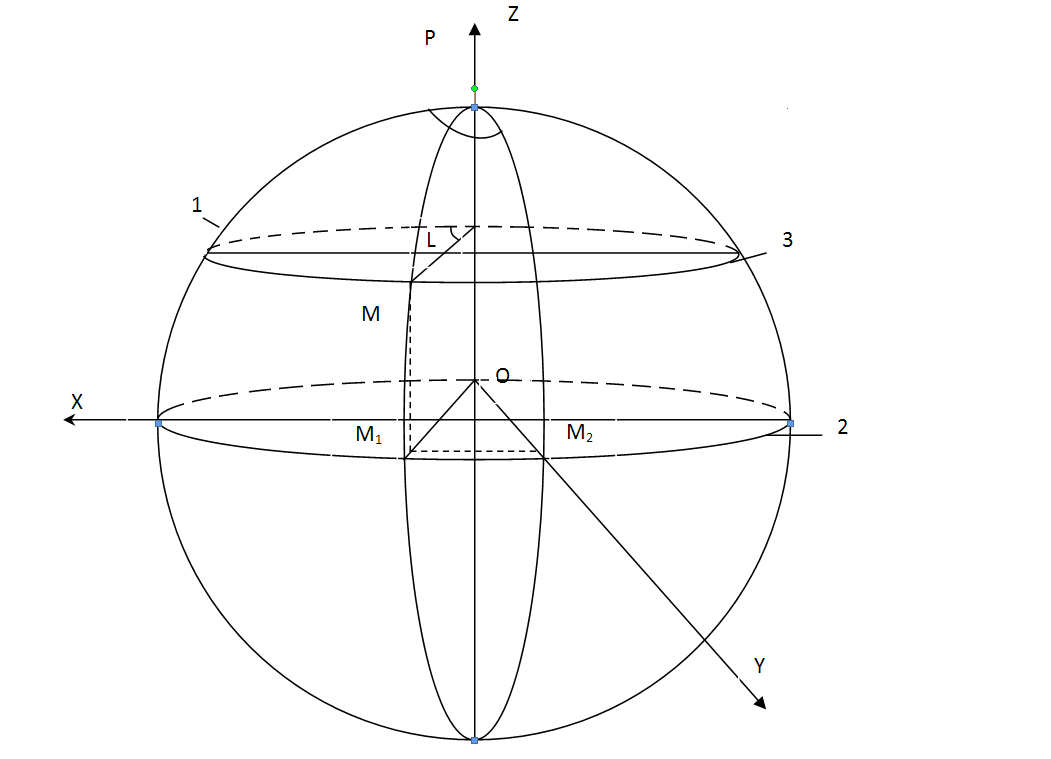
1 – Гринвичский меридиан;
2 – плоскость экватора;
OZ направлена по полярной оси эллипсоида;
OY расположена в плоскости экватора, 90◦ начального меридиана;
M лежит на поверхности эллипсоида;
3 – параллель точки M;
L – геодезическая долгота.
Из точки М проведем линию параллельную ОР, получим точку М1; проведем линию параллельную ОХ, получим точку М2.
Координаты точки М:
Хм = М1М2;
Yм = ОМ2;
Zм = ММ1.
Достоинство этой системы координат – можно использовать в космической геодезии.
| Y |
| P |
| M |
| x |
| R1 |
| y |
| MΙ |
| R |
| O |
xmax = a
| X |
PR1P1R – меридианный эллипс,
проходящий через точку M.
| P1 |
Для практических вычислений координаты в этой системе не используются.
3. Система геодезических координат:
| P |
| L |
| M |
| β |
| n |
| R |
| O |
точки M;
L – геодезическая долгота;
B – геодезическая широта;
| P1 |
n – пересечение нормали с осью эллипсоида.
Это основная система сфероидической геодезии.
Достоинства этой системы координат:
- система едина для всей поверхности эллипсоида;
- не требует дополнительных построений, так как координатные линии это параллели и меридианы;
- определяет положение нормали в данной точке, а это важно при изучении уклонений отвесных линий.
В пространственных координатах здесь используется H – высота точки над эллипсоидом.
H – отрезок нормали от точек физической поверхности до точки на эллипсоиде.
| P |
| M |
| r |
| φ |
| O |
| P1 |
r – геоцентрический радиус -
вектор;
φ – геоцентрическая щирота;
| Y |
| B |
| u |
| φ |
| y |
| M |
| x |
| n |
| X |
| M’ |
2 – окружность с центром в т.О;
u – приведенная широта;
В – геодезическая широта;
ОМ = r – геоцентрический радиус-
вектор.
4. Связь между разными системами координат.
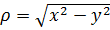 (6)
(6)
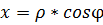 ;
; 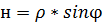 (7)
(7)
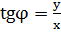 (8)
(8)
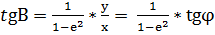 (9)
(9)
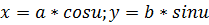 (10)
(10)
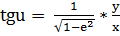 (11)
(11)
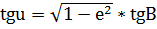 (12)
(12)
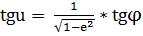 (13)
(13)
Из формулы 9 следует, что 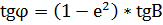 (14)
(14)
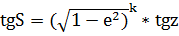 (*), где S и Z отвлеченные величины, а в зависимости от k можно получить формулы с 11-ой по 14-ую.
(*), где S и Z отвлеченные величины, а в зависимости от k можно получить формулы с 11-ой по 14-ую.
| S | Z | k | формулы |
| u | B | 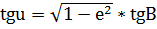 (12) (12)
| |
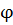
| u | 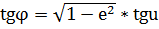 (13) (13)
| |
| B | u | -1 | 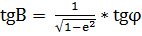 (12) (12)
|
| u | 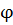
| -1 |  (13) (13)
|
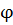
| B | 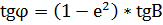 (14) (14)
| |
| B | 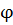
| -2 | 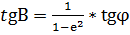 (14) (14)
|
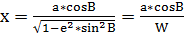 , где W – первая функция широты.
, где W – первая функция широты.
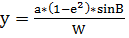 (15)
(15)
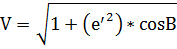 , где V – вторая функция широты.
, где V – вторая функция широты.
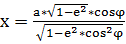 ,
, 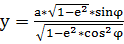 ;
;
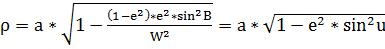 .
.
5. Связь между различными системами координат в пространстве.
Рассмотрим пространственную геоцентрическую систему координат.
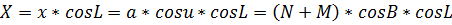
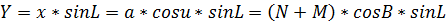
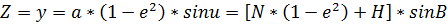
L – долгота;
x, y – меридианные координаты эллипса;
а – большая полуось эллипсоида;
е – эксцентриситет эллипсоида;
u – приведенная широта;
N – радиус кривизны первого вертикала;
H – геодезическая высота;
B – геодезическая широта.
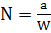 , где W – первая основная функция геодезической широты.
, где W – первая основная функция геодезической широты.
M – радиус кривизны меридиана: 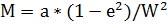
Радиус кривизны произвольного нормального сечения:
 , где А – азимут.
, где А – азимут.
Ro◦ = M; R90◦ = N
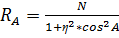 ;
;  ;
;
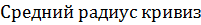 ны:
ны:
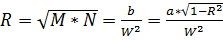 ;
;
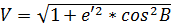 следовательно, N=c/V, где с – полярный радиус кривизны меридиана.
следовательно, N=c/V, где с – полярный радиус кривизны меридиана.
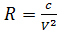 ;
; 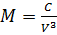
Неравенство N<R<M используется для контроля вычислений.
Рассмотрим формулы перехода от Х,Y,Z к B,L,H и обратно.
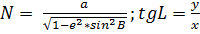
Для определения четверти L (смотреть рисунок):
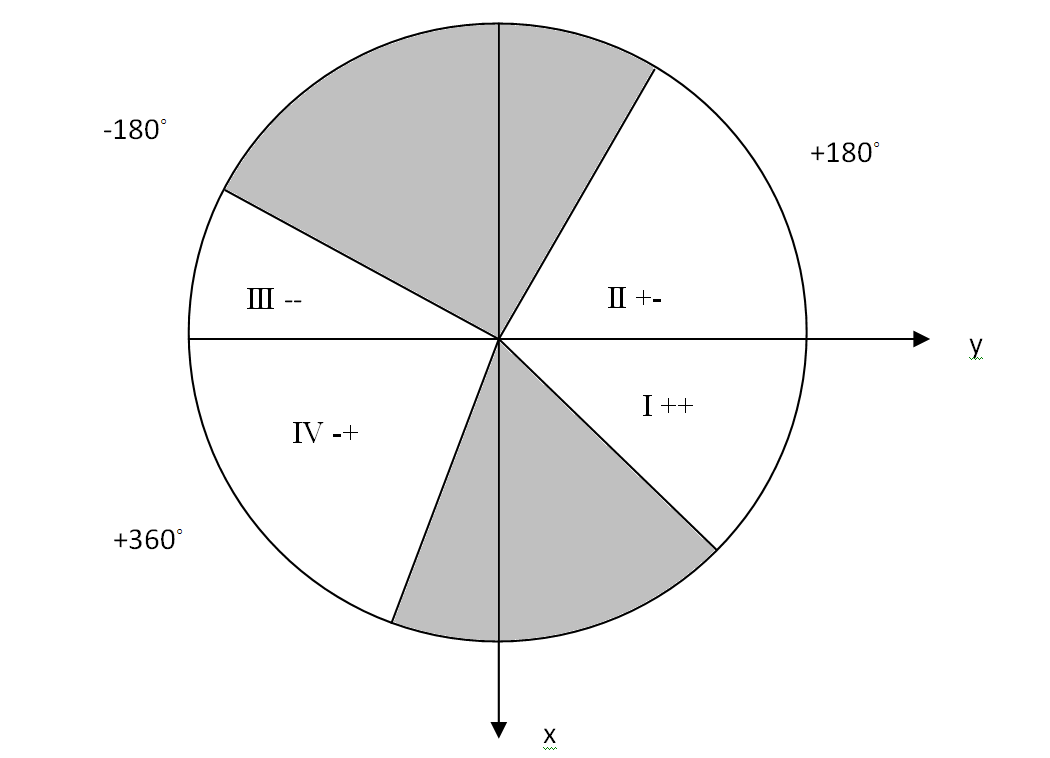
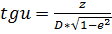 (15) , где
(15) , где 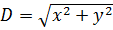
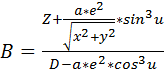 (16)
(16)
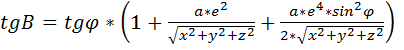 , где
, где 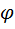 - геоцентрическая широта,
- геоцентрическая широта, 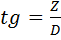 (17)
(17)
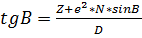 (18) – требуется до пяти приближений.
(18) – требуется до пяти приближений.
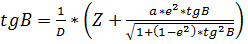 (19)
(19)
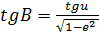 (20)
(20)
Подставив формулу (20) в формулу (15) получим:
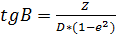 (21)
(21)
6. Длинна дуги меридиана.
dS = M*dB, где dS – малое расстояние на эллипсоиде по меридиану; M – радиус кривизны меридиана, dB – малая разность широт.
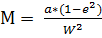 ,
, 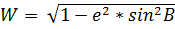
От дифференциального уравнения перейдем к интегральному. Интегрируем по S и B:
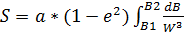 ;
;
Это эллиптический интеграл, следовательно, для его нахождения применим ряд:
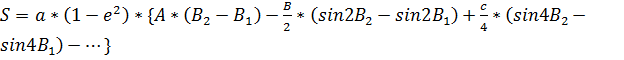
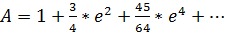 универсальные формулы для любых
универсальные формулы для любых
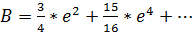 размеров эллипсоида
размеров эллипсоида
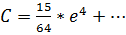
Для средней широты 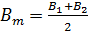 имеем:
имеем:
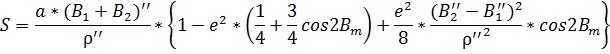
удобно пользоваться в градусных измерениях.
Для расстояний 400 км:
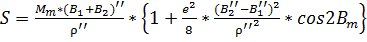
дает ошибку в длине 1мм.
Для расстояний меньше 45 км:
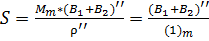 , где
, где 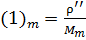 и
и 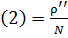 , где N – радиус кривизны первого вертикала.
, где N – радиус кривизны первого вертикала.
7. Вычисление длинны дуги параллели.
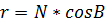 - радиус параллели;
- радиус параллели;
B – широта;
N – радиус кривизны первого вертикала;
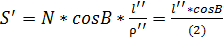
l’’ – разность долгот в секундах.
l’’=(2)*S’*secB.
8. Расчет рамок съемочных трапеций.
| А |
| С |
| В2 |

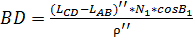
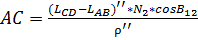
| В1 |
| В |
| D |
Площадь трапеции:
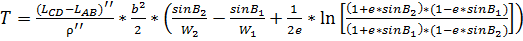
e – основание натурального логарифма;
b – малая полуось.
9. Кривые на эллипсоиде вращения.
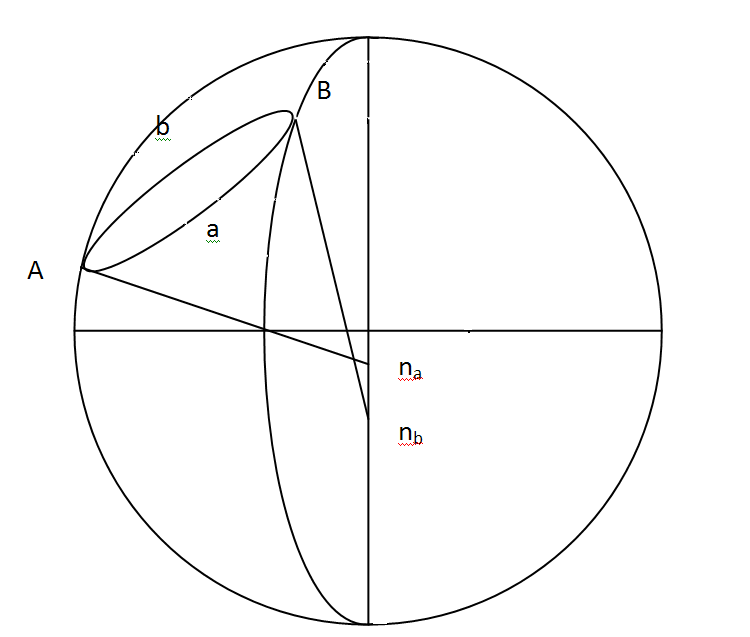 A,Б – точки на эллипсоиде на
A,Б – точки на эллипсоиде на
разных меридианах;
Аna – нормаль к эллипсоиду
в точке А;
Bnb – нормаль к эллипсоиду
в точке B;
Проведём плоскость через три точки АnаВ. В этой плоскости лежит нормаль Аnа. Эта плоскость называется нормальной плоскостью в точке А, проходящей через точку В. Кривая АаВ есть прямое нормальное сечение в точке А на точку В.
Плоскость, проходящая через три точки BnbА, образует на эллипсоиде нормальное сечение из точки В на точку А. Это новая плоскость оставит след на эллипсоиде b.
Кривая BbA будет не совпадать с а. b – называется кривая обратного нормального сечения.
а не совпадает с b потому что нормали Аnа и Bnb не лежат в одной плоскости. Нетрудно заметить, что несовпадение прямых и обратных нормальных сечений приводит к тому, что измеренные горизонтальные углы на трех пунктах не образуют на поверхности эллипсоида замкнутого треугольника, фигура получится разорванной.
| В сфероидической геодезии точки на поверхности эллипсоида соединяются геодезическими линиями (это кратчайшее расстояние между двумя точками). Из дифференциальной геометрии известно, что в каждой точке геодезической линии главная нормаль совпадает с нормалью к поверхности. |
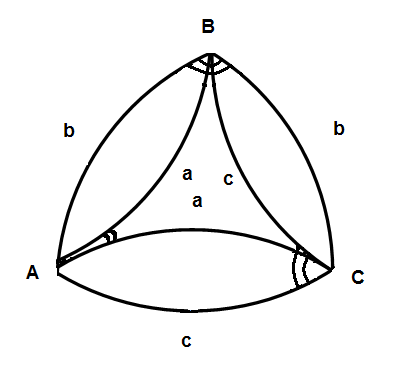
Если треугольник будет состоять из геодезических линий, то фигура не будет разорванной.
| Δ – угол между взаимообратными сечениями. δ – угол между геодезической линией и прямым нормальным сечением |
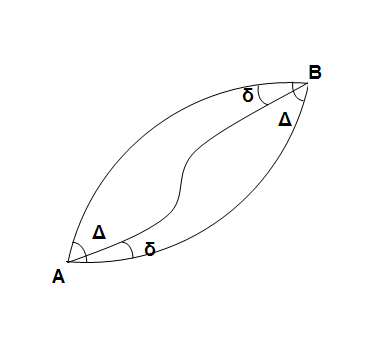
При этом геодезическая линия на поверхности эллипсоида делит угол Δ в отношении 1:2 и располагается ближе к прямому нормативному сечению, то есть 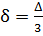 .
.
Из теоремы Клеро известно:
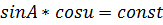 , где А – азимут; u – приведенная широта.
, где А – азимут; u – приведенная широта.
Зная, что 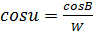 , можем записать:
, можем записать:
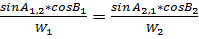
Исходя из этой формулы, запишем в окончательном виде формулу для вычисления 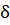 :
:
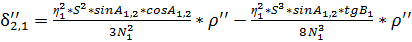
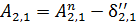 ;
;
Здесь An – азимут нормального сечения.
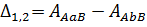 ;
;
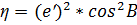
Решение малых сферических и сфероидических треугольников.
Для сферического треугольника:
А+С+В=180◦ + Ɛ, где Ɛ – сферический избыток.
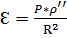 , где P – площадь треугольника, R – средний радиус кривизны эллипсоида на район работ. , где P – площадь треугольника, R – средний радиус кривизны эллипсоида на район работ.
|
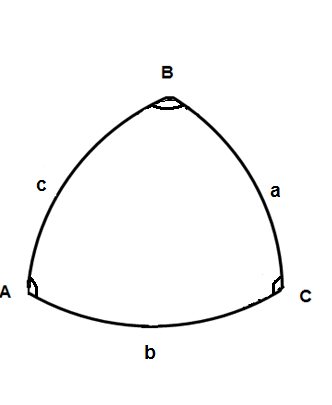
Введем обозначения:
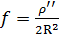 ,тогда
,тогда
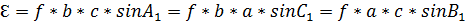
A1, B1, C1 – плоские приведенные углы.
По теореме Лежандра:
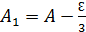 ;
;
 ;
;
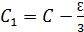 .
.
Если треугольник с большими сторонами, то его следует рассматривать как сфероидический треугольник:
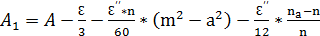 ;
;
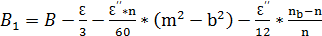 ;
;
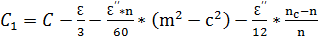 .
.
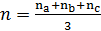 ;
;
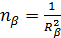 – гаусова кривизна вершин треугольника ABC.
– гаусова кривизна вершин треугольника ABC.
S – стороны равностороннего треугольника,
если S = 60 км, то Ɛ = 8’’;
если S = 30 км, то Ɛ = 2’’;
если S = 20 км, то Ɛ = 1’’;
если S = 10 км, то Ɛ = 0,25’’;
если S = 5 км, то Ɛ = 0,07’’.
Решение треугольника по теореме Лежандра:
| Измеренные углы | 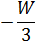
| Уравненные сферические углы. | 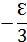
| Углы плоского треугольника | sin 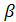
| Стороны сферического треугольника |
| Bизм | b известно | |||||
| Aизм | a | |||||
| Cизм | c | |||||
| Ʃ=180◦ +Ɛ | Ʃ=180◦ |
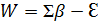
Применение способа аддитаментов:
| Измеренные углы | 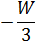
| Уравненные сферические углы | 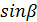
| Приближен.стороны | Аддита-менты | Стороны сферич.тре-угольника |
| Bизм | b’ | Ab | b известно | |||
| Aизм | a’ | Aa | a | |||
| Cизм | c’ | Ac | c | |||
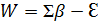
|
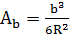 ;
; 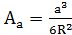 ;
; 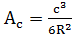 ;
;
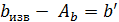 ;
;
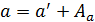 ;
;
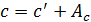 .
.
Общие сведения о вычислении широт, долгот и азимутов.
Будем рассматривать задачу вычисления координат точек на поверхности эллипсоида вращения.
Здесь изучим методы вычисления геодезических координат.
На плоскости:
Прямая задача: Дано:x1,y1,S,α
Найти: x2,y2
Обратная задача: Дано:x1,y1,S,α
Найти: x2,y2
На эллипсоиде:
Прямая задача: Дано: B1,L1,S1,2,A1,2
Найти: B2,L2, A2,1
Обратная задача: Дано: B1,L1,B2,L2
Найти: S1,2,A1,2, A2,1
Прямая и обратная задачи называются главными геодезическими задачами.
Рассмотрим расстояние S1,2:
Они бывают: малые – 30-45 км;
средние – 300 км;
большие – до 5000 км;
очень большие – до 19000 км.
| A,B – точки на эллипсоиде; Р – полюс; РА и РВ – меридианы; l – разность долгот такая, что L2 = L1 + l. Для решения главное геодезической задачи используют два пути: - прямой; - косвенный. |
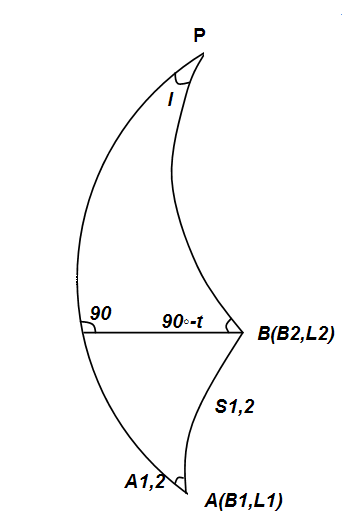
Прямой путь решения: решаем сфероидический треугольник PAB.
Косвенный путь: вычисляем разности:
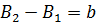 ;
;
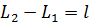 ;
;
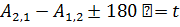
Тогда во втором косвенном пути:
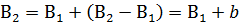 ;
;
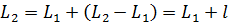 ;
;
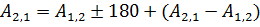 .
.
Поговорим о точности вычислений:
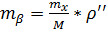 , где
, где 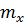 - точность положения на плоскости;
- точность положения на плоскости;
M – радиус кривизны меридиана;
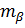 - ошибка широты.
- ошибка широты.
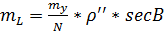
если 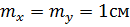 , то
, то 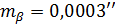 , следовательно
, следовательно 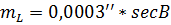 ,
, 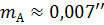
При расстояниях 25 км вычисления B и L требуется выполнить с семью значными цифрами, а азимут А до сотых.
Рассмотрим формулы решения прямой геодезической задачи косвенным способом:
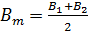 ,
, 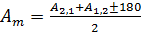 – средняя широта и азимут.
– средняя широта и азимут.
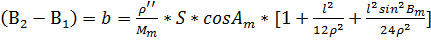
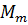 -радиус кривизны меридиана для средней широты.
-радиус кривизны меридиана для средней широты.
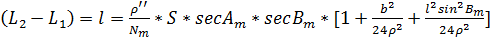
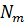 – радиус кривизны первого вертикала.
– радиус кривизны первого вертикала.
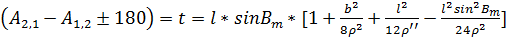
Для решения этой задачи необходимы приближения.
Обратная геодезическая задача:

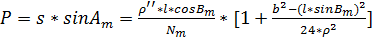
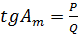
расстояние 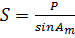 , контроль
, контроль 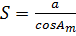 ,
,
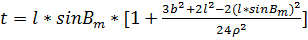
Решение главной геодезической задачи по способу Бесселя.
Задача решается на эллипсоиде путем конформного преобразования на поверхности шара.
Сделаем чертеж:
| На эллипсоиде: AB – длина геодезической линии; l – разность долгот. |
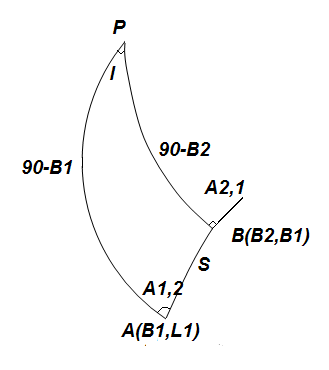
На шаре имеем 3 точки.
| δ – длина стороны на шаре; u1,u2 – приведенные широты; m – сторона прямоугольного сферического треугольника. |
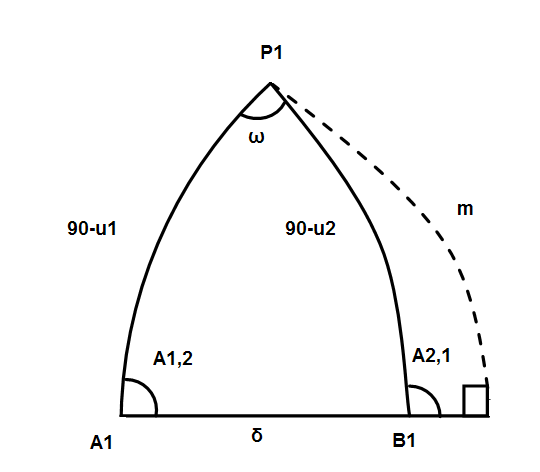
Рассмотрим решение прямой геодезической задачи на эллипсоиде:
По теореме Клеро:
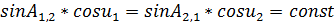

δ – зависит от δ, т.е. задача решается методом приближений.
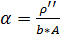 ,
,  ,
, 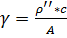 ;
;
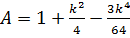 ;
;
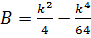 ;
;
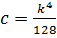 ;
;
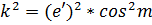 ;
;
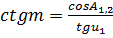 ;
;
В первом приближении 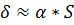
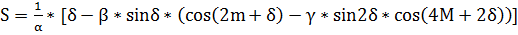 (Ф.1)
(Ф.1)
Далее вычисляют 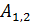 ,w, и u2 по формулам:
,w, и u2 по формулам:
Из треугольника A1P1B1 вычисляют 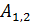 ,w, и u2 по двум сторонам 90-u,
,w, и u2 по двум сторонам 90-u, 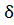 и углу A2.
и углу A2.
Далее находят разность долгот:
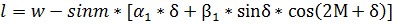 (Ф.2)
(Ф.2)
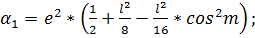
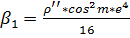 ;
;
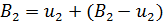
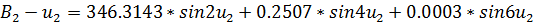 (Ф.3)
(Ф.3)
Решение обратной геодезической задачи по способу Весселя:
1) 
2) 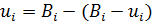 .
.
разность 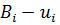 находим по формуле Ф.3.
находим по формуле Ф.3.
3) Вычислим w по формуле Ф.2.
4) Находим А1,2 и А2,1 из сферического треугольника A1P1B1
5) Находим сторону S по формуле Ф.1.
Это единственный способ позволяющий решать задачи до 20000 км.
Дата добавления: 2015-08-11; просмотров: 3118;
