Действующие и средние значения периодических ЭДС и токов

Понятие о среднем квадратичном (действующем) значении можно получить, рассматривая тепловое действие тока. Пусть сопротивление цепи, в которой протекает периодический ток, равно R. Тогда согласно закону Джоуля – Ленца количество теплоты, выделяемой в этом сопротивлении за элементарный промежуток времени dt, будет равно , а за один полный период – .

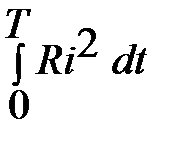Обозначим через I такой постоянный ток, который за промежуток времени Т выделит в со­противлении R такое же количество тепла. Тогда имеем:

, откуда .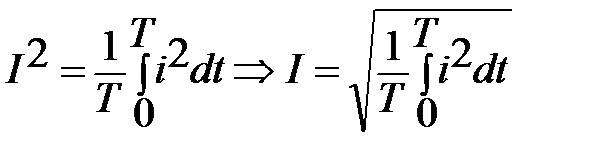

Величина I, определяемая последним ра­венством, называется действующимили сред­ним квадратичнымзначением периодического тока.

Для синусоидального тока имеем: и, следовательно,

.

Аналогично определяется действующее значение периодической синусоидальной ЭДС:

.

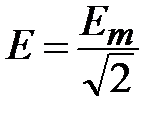Приборы, применяемые для измерения пе­риодических ЭДС (токов), показывают их действующие значе­ния.

Кроме действующих значений периодических ЭДС (токов), используют их средние зна­чения.

Под среднимзна­чением гармонически изменяющегося тока (ЭДС) понимают значение соответствующее положительной полуволне:

.

Аналогично .

Для гармонических функций:

коэффициент амплитуды - это отношение амплитудного значения тока (ЭДС) к действующему значению: ;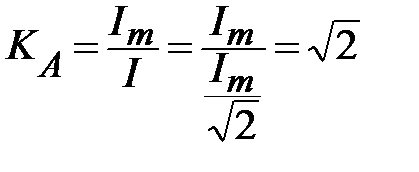

коэффициент формы - это отношение действующего значения тока (ЭДС) к среднему значению: .