Модуль 7. СТАТИСТИЧЕСКОЕ ИЗУЧЕНИЕ ВЗАИМОСВЯЗЕЙ
Комплексная цель.
Изучение теоретических основ и методики корреляционного и регрессионного анализа.
Содержание.
Основные понятия корреляционного и регрессионного анализа
Исследуя природу, общество, экономику, необходимо считаться со взаимосвязью наблюдаемых процессов и явлений. При этом полнота описания так или иначе определяется количественными характеристиками причинно-следственных связей между ними. Оценка наиболее существенных из них, а также воздействия одних факторов на другие является одной из основных задач статистики.
В основу классификации многообразия связей в экономике обычно кладут тесноту связи между результативными и факторными показателями, характер связи, вид уравнения, используемого в качестве математической модели изучаемой связи, количество факторов.
В зависимости от тесноты связи подразделяют на функциональные и корреляционные, от характера — на прямые и обратные, от вида уравнений - на прямолинейные и криволинейные, от числа факторов — на однофакторные и многофакторные.
Формы проявления взаимосвязей весьма разнообразны. В качестве двух самых общих их видов выделяют функциональную (полную) и корреляционную (неполную) связи. В первом случае величине факторного признака строго соответствует одно или несколько значений функции. В экономике примером может служить прямо пропорциональная зависимость между производительностью труда и увеличением производства продукции. Для функциональных связей характерным является ограниченное число факторов, что обеспечивает их сравнительную простоту. Другая их особенность - устойчивость. Факторы здесь в одинаковой степени проявляются во всех случаях независимо от изменения других признаков исследуемого явления.
Корреляционная связь (которую также называют неполной, или статистической) проявляется в среднем, для массовых наблюдений, когда заданным значениям зависимой переменной соответствует некоторый ряд вероятных значений независимой переменной. Объяснение тому - сложность взаимосвязей между анализируемыми факторами, на взаимодействие которых влияют неучтенные случайные величины. Поэтому связь между признаками проявляется лишь в среднем, в массе случаев. При корреляционной связи каждому значению аргумента соответствуют случайно распределенные в некотором интервале значения функции.
Например, некоторое увеличение аргумента повлечет за собой лишь среднее увеличение или уменьшение (в зависимости от направленности) функции, тогда как конкретные значения у отдельных единиц наблюдения будут отличаться от среднего. Такие зависимости встречаются повсеместно. Например, в сельском хозяйстве это может быть связь между урожайностью и количеством внесенных удобрений. Очевидно, что последние участвуют в формировании урожая. Но для каждого конкретного поля, участка одно и то же количество внесенных удобрений вызовет разный прирост урожайности, так как во взаимодействии находится еще целый ряд факторов (погода, состояние почвы и др.), которые и формируют конечный результат. Однако в среднем такая связь наблюдается - увеличение массы внесенных удобрений ведет к росту урожайности. Экономические показатели складываются под влиянием множества объективных и субъективных факторов. Поскольку учет всех факторов, влияющих на результативные показатели, практически невозможен, закономерности, устанавливаемые в экономике, не являются точными и устойчивыми. Поэтому при исследовании взаимосвязей экономических показателей используют корреляционные зависимости.
Будучи неполными и устойчивыми, корреляционные связи не могут быть установлены по данным единичного исследования, а только по результатам массовых наблюдений. И если в функциональных связях количество учитываемых факторов является ограниченным, то в корреляционных оно может быть довольно значительным.
По направлению связи бывают прямыми, когда зависимая переменная растет с увеличением факторного признака, и обратными, при которых рост последнего сопровождается уменьшением функции. Такие связи также можно назвать соответственно положительными и отрицательными.
Относительно своей аналитической формы связи бывают линейными и нелинейными. В первом случае между признаками в среднем проявляются линейные соотношения. Нелинейная взаимосвязь выражается нелинейной функцией, а переменные связаны между собой в среднем нелинейно.
Существует еще одна достаточно важная характеристика связей с точки зрения взаимодействующих факторов. Если характеризуется связь двух признаков, то ее принято называть парной. Если изучаются более чем две переменные - множественной.
Указанные выше классификационные признаки наиболее часто встречаются в статистическом анализе. Но кроме перечисленных различают также непосредственные, косвенные и ложные связи. Собственно, суть каждой из них очевидна из названия. В первом случае факторы взаимодействуют между собой непосредственно. Для косвенной связи характерно участие какой-то третьей переменной, которая опосредует связь между изучаемыми признаками. Ложная связь - это связь, установленная формально и, как правило, подтвержденная только количественными оценками. Она не имеет под собой качественной основы или же бессмысленна.
По силе различаются слабые и сильные связи. Эта формальная характеристика выражается конкретными величинами и интерпретируется в соответствии с общепринятыми критериями силы связи для конкретных показателей.
В наиболее общем виде задача статистики в области изучения взаимосвязей состоит в количественной оценке их наличия и направления, а также характеристике силы и формы влияния одних факторов на другие. Для ее решения применяются две группы методов, одна из которых включает в себя методы корреляционного анализа, а другая - регрессионный анализ. В то же время ряд исследователей объединяет эти методы в корреляционно-регрессионный анализ, что имеет под собой некоторые основания: наличие целого ряда общих вычислительных процедур, взаимодополнения при интерпретации результатов и др.
Поэтому в данном контексте можно говорить о корреляционном анализе в широком смысле - когда всесторонне характеризуется взаимосвязь. В то же время выделяют корреляционный анализ в узком смысле - когда исследуется сила связи - и регрессионный анализ, в ходе которого оцениваются ее форма и воздействие одних факторов на другие.
Задачи собственнокорреляционного анализа сводятся к измерению тесноты связи между варьирующими признаками, определению неизвестных причинных связей и оценке факторов оказывающих наибольшее влияние на результативный признак.
Задачирегрессионного анализа лежат в сфере установления формы зависимости, определения функции регрессии, использования уравнения для оценки неизвестных значении зависимой переменной.
Решение названных задач опирается на соответствующие приемы, алгоритмы, показатели, применение которых дает основание говорить о статистическом изучении взаимосвязей.
Следует заметить, что традиционные методы корреляции и регрессии широко представлены в разного рода статистических пакетах программ для ЭВМ. Исследователю остается только правильно подготовить информацию, выбрать удовлетворяющий требованиям анализа пакет программ и быть готовым к интерпретации полученных результатов. Алгоритмов вычисления параметров связи существует множество, и в настоящее время вряд ли целесообразно проводить такой сложный вид анализа вручную. Вычислительные процедуры представляют самостоятельный интерес, но знание принципов изучения взаимосвязей, возможностей и ограничений тех или иных методов интерпретации результатов является обязательным условием исследования.
Методы оценки тесноты связи подразделяются на корреляционные (параметрические) и непараметрические. Параметрические методы основаны на использовании, как правило, оценок нормального распределения и применяются в случаях, когда изучаемая совокупность состоит из величин, которые подчиняются закону нормального распределения. На практике это положение чаще всего принимается априори. Собственно, эти методы - параметрические - и принято называть корреляционными.
Непараметрические методы не накладывают ограничений на закон распределения изучаемых величин. Их преимуществом является и простота вычислений.
Производственные функции. Исследуемые корреляционные связи в экономике также называют экономико-статистическими. Их круг является довольно обширным. Среди них особое место занимают связи, которые определяют уровень производственных показателей. Такие связи получили название производственных функций. Таким образом, производственная функция — это экономико-статистическая модель связи, характеризующая изменение уровня результативных производственных показателей в зависимости от одного или ряда важнейших производственных факторов. Например, это функции производства продукции от затрат различных ресурсов, функции издержек от количества полученной продукции, функции производительности труда от фондо- и энерговооруженности, функции урожайности от доз внесения удобрений, функции продуктивности животных от уровня их кормления и т. д.
Способы задания производственных функций. Производственные функции задаются различными способами. Наиболее распространенным является аналитический способ. Производственная функция при аналитическом выражении представляет собой математическое уравнение, моделирующее зависимость результативного экономического показателя от одного или ряда производственных факторов. Например, наиболее типичной формой кривой динамики цен на отдельные продукты является функция
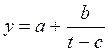
где а - минимальный уровень цен;
b, с - постоянные параметры процесса;
t - время в годах.
Преимуществом аналитического способа являются его компактность, легкая воспроизводимость и приспособленность к выполнению над функциями ряда математических действий. К его недостаткам следует отнести отсутствие наглядности и то, что для определения значений результативных показателей необходимо выполнить ряд вычислений, и к тому же не всегда простых.
Табличный способ задания производственных функций заключается в представлении результативного показателя, соответствующего определенным значениям факторов, в виде таблицы. Заранее вычисленными значениями функций можно быстро воспользоваться в любое время, что позволяет более оперативно решать вопросы анализа и планирования сельскохозяйственного производства. Чаще всего составляют таблицы с каким-то определенным шагом. При необходимости определения уровня результативного показателя при значениях факторов, отсутствующих в таблице, прибегают к интерполяции, когда значения факторов промежуточные, и к экстраполяции, когда они находятся за пределами таблицы. Это один из недостатков табличного способа; к другому недостатку относится его некомпактность, поскольку таблицы часто занимают большой объем, особенно когда они имеют несколько входов.
Нередко производственные функции задаются графическим способом. Здесь зависимость исследуемого показателя от фактора представляется в виде графика. Его построение обычно ведется в прямоугольной системе координат на основе аналитического выражения функции или ее табулированных значений. Преимуществом графического способа является наглядность, недостатком - невысокая точность, которую можно повысить выбором соответствующего масштаба. К недостаткам относится и то, что возможности способа ограничены только одним фактором.
Классификация производственных функций. Производственных функций существует большое множество. Любая, в достаточной мере изученная закономерность, зависимость может быть смоделирована производственной функцией. Статистико-экономические зависимости (производственные функции) можно классифицировать по целому ряду признаков.
С точки зрения степени влияния человека на исследуемый результативный показатель производственные функции бывают объективными, субъективными и объективно-субъективными. Объективные - это такие связи, которые не зависят от воли людей.
Субъективные же связи определяются целенаправленной деятельностью человека, его сознанием, волей, умением. Находят практическое применение и смешанные объективно-субъективные производственные функции. К таким функциям относится, например, зависимость урожая культуры от метеорологических факторов (температуры, осадков) и количества вносимых органических и минеральных удобрений.
По признаку сложности производственные функции можно разделить на две группы: простые и сложные. Простые - это немногофакторные, элементарные зависимости. Сложные производственные функции моделируют зависимости от целого ряда факторов, которые в определенной мере взаимосвязаны друг с другом.
Производственные функции по степени полноты учета факторных признаков делят на закрытые и открытые. Простые детерминированные зависимости являются закрытыми. Здесь не возникает необходимости ввода новых факторов. Большинство сложных стохастических производственных функций составляют группу открытых зависимостей. Со временем, по мере углубления исследований, в такие производственные функции вводятся новые факторы, и они могут переходить в группу закрытых.
Возможен и обратный процесс, т.е. превращение закрытой производственной функции в открытую. Это происходит в случае неполного разложения факторного признака на ряд подфакторов. Поэтому простая, детерминированная, закрытая производственная функция становится открытой.
Производственные функции строят по данным как вариационных, так и динамических рядов. Нередко встречаются зависимости, полученные в результате обработки информации предприятий за ряд лет. Поэтому можно считать, что производственные функции бывают вариационные, динамические и вариационно-динамические. Следует отметить, что зависимости, моделирующие тенденции изменения экономических показателей во времени, принято именовать трендами. Их определяют в целях анализа и разработки экономико-математических моделей прогнозирования уровня экономических показателей.
Если исходить из числа факторов, учтенных в модели, то производственные функции делят на одно- и многофакторные.
В зависимости от "вида математической модели производственные функции делят на линейные и криволинейные.
Направление влияния факторных признаков на зависимый показатель бывает прямое, обратное и комбинированное. Сообразно этому и производственные функции делят на прямые, обратные и комбинированные.
Когда производственная функция получена в результате обработки данных выборки, то она именуется выборочной. Генеральная производственная функция — это зависимость, построенная с учетом всей генеральной совокупности.
Производственные функции строят по однолетним и многолетним данным. В связи с этим экономико-статистические зависимости можно подразделить на однопериодные и многопериодные. Периодом может быть месяц, квартал, год, пятилетка и т. п.
Статистико-экономические зависимости составляются на основе информации в целом по народному хозяйству, по его от дельным отраслям, по каким-то регионам, по конкретным хозяйствам, по их объединениям и подразделениям. Поэтому производственные функции бывают: межотраслевыми, отраслевыми, региональными, межхозяйственными и хозяйственными. Производственные функции, построенные на уровне народного хозяйства, именуют макроэкономическими. Модели, полученные в результате обработки информации предприятий, их подразделений и объединений, называют микроэкономическими.
Классификация производственных функций
| Классификационные признаки | Виды производственных функций |
| Степень влияния человека | Объективные Субъективные Объективно-субъективные |
| Теснота зависимости | Детерминированные Стохастические |
| Сложность связей | Простые Сложные |
| Полнота учета факторов | Закрытые Открытые |
| Вид ряда данных | Вариационные Динамические Вариационно-динамические |
| Число факторов | Однофакторные Многофакторные |
| Вид математической модели | Линейные Криволинейные |
| Направление влияния факторов | Прямые Обратные Комбинированные |
| Полнота учета информации | Выборочные Генеральные |
| Временной фактор | Однопериодные Многопериодные |
| Уровень управления | Межотраслевые Отраслевые Региональные Межхозяйственные Хозяйственные |
Виды производственных функций. Вид производственной функции определяется видом уравнения, которое используется в качестве ее математической модели. Поскольку на многие результативные показатели оказывают весьма различное влияние множество производственных факторов как по величине, так и по направлению, то моделирование таких процессов может осуществляться также с помощью большой совокупности математических уравнений.
В математике имеется много разных уравнений, которые могут имитировать динамику и зависимость исследуемых результативных показателей от ряда производственных факторов. Но положение с моделированием статистико-экономических зависимостей осложняется рядом обстоятельств.
Одно и то же математическое уравнение как математическая модель может использоваться для построения нескольких (различных) зависимостей.
Одна и та же производственная связь может имитироваться разными математическими уравнениями.
Апробированные математические модели с изменением места и времени часто оказываются практически неприемлемыми.
Идеальной производственной функцией следует считать ту, которая наиболее точно воспроизводит исследуемое явление или процесс. Но построение таких идеальных статистико-экономических моделей возможно только в простейших случаях.
С развитием науки и техники, с внедрением достижений научно-технического прогресса применение производственных функций будет все более эффективным. Это станет достигаться по-видимому путем вскрытия новых реальных зависимостей, закономерностей, законов; посредством разработки и внедрения более совершенных много факторных и динамических производственных функций; вследствие более результативного использования математических методов и ЭВМ.
Наиболее простой однофакторной статистико-экономической зависимостью является линейная функция  .
.
Эта функция моделирует прямую пропорциональную зависимость. Ее графиком является прямая, которая проходит через начало координат. Число {а) называется угловым коэффициентом прямой. С помощью этой производственной функции моделируют зависимость, например, стоимости продукции (у) от ее количества или цены ее единицы (jc).
На практике чаще используют линейную производственную функцию вида
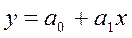
Линейная производственная функция моделирует зависимость, например, уровня оплаты труда (у) от его производительности (х).
Широкое распространение в экономических исследованиях получила производственная функция, моделью которой является парабола второго порядка
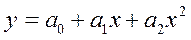
Производственную функцию целесообразно использовать для моделирования зависимостей, имеющих одну экстремальную точку (точку минимума или максимума). Такой является, например, зависимость урожая культуры (у) от внесения удобрений (jc). С увеличением количества применяемых удобрений урожайность повышается, при высоких дозах ее рост замедляется.
В некоторых случаях прибегают к целой рациональной функции вида
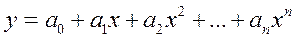
Эту функцию используют тогда, когда исследуемая зависимость содержит ряд экстремумов.
Для моделирования обратных пропорциональных зависимостей применяют производственную функцию
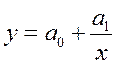
Ее графиком является гипербола, сдвинутая по оси ординат на а0. Производственная функция хорошо моделирует зависимость, например, издержек на единицу продукции (у) от производительности оборудования (х).
С целью более точного описания исследуемой зависимости прибегают к функции вида
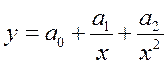
Правомерным является также использование обратной рациональной функции
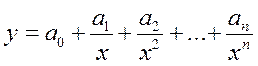
В последние годы находит практическое применение следующая степенная функция:
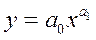
График этой функции напоминает кривую 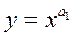 , точки которой сдвинуты по оси ординат в зависимости от величины а0.
, точки которой сдвинуты по оси ординат в зависимости от величины а0.
Анализируя ряды динамики и исследуя уровень важнейших экономических параметров предприятия, часто используют показательную производственную функцию
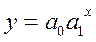
Для моделирования периодических, сезонных колебаний, волнообразных процессов применяют различные тригонометрические уравнения. Простейшими из них являются следующие уравнения синусоиды:

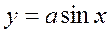
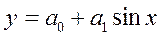
Опыт свидетельствует о целесообразности использования, например, уравнения в качестве модели производственной функции, выражающей зависимость трудовой активности (у) водителей автомобилей и других работников от месяца года (х). Порядковый месяц года (х) в производственной функции фигурирует как аргумент в радианах. Находят применение и более сложные тригонометрические функции.
Разумеется, выше приведены далеко не все виды однофакторных производственных функций. В реальной действительности однофакторные зависимости имеют незначительный удельный вес. В большинстве связи и зависимости многофакторные. Но в анализе, прогнозировании, планировании и в научных исследованиях предпочтение пока что отдается однофакторным производственным функциям. Однако в будущем использование многофакторных зависимостей станет, безусловно, превалирующим.
Видов многофакторных производственных функций можно привести очень много. По аналогии с однофакторными зависимостями они бывают прямыми, обратными, комбинированными, степенными, показательными, логарифмическими, геометрическими, тригонометрическими; могут сочетать различные виды уравнений и т. д. Приведем несколько основных видов множественных зависимостей. Наиболее распространенной из них является многофакторная линейная функция

Она моделирует, например, зависимость себестоимости производства единицы продукции (у) от затрат различных ресурсов в расчете на единицу измерения отрасли.
Правомерно применение и обратной многофакторной функции
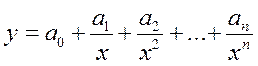
Эффективным является использование многофакторных парабол второго порядка. Для примера приведем такую двухфакторную зависимость:
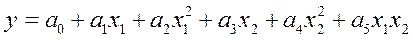
Вопрос о предпочтительности какой-то зависимости решается исходя из аналитических характеристик построенных производственных функций. Иногда одновременно используют ряд производственных функций, полученных в результате обработки одной и той же информации, что дает возможность выполнять их сравнительный анализ и оценку.
Приведенные многофакторные производственные функции далеко не исчерпывают все их множество.
Основные направления использования производственных функций. Сейчас трудно назвать такую область человеческой деятельности, где не могли бы применяться статистико-экономические зависимости или производственные функции. Одни из основных направлений их использования следующие.
1. Определение влияния различных факторов на анализируемые результативные показатели. Именно с данного направления и начинается история развития исследований производственных функций.
Чаще всего для этого используют линейные одно- и много факторные зависимости, коэффициенты которых в опреде ленной мере характеризуют абсолютное влияние факторных признаков. Находят применение и другие производственные функции.
2. Поиск оптимального сочетания факторов. Наилучшей, оптимальной именуют такую комбинацию факторных признаков, при которой зависимый показатель достигает экстремального (максимального или минимального) уровня. Это очень важная экономическая задача. В экономических системах весьма часто складываются такие ситуации, когда объемы производственных ресурсов находятся далеко не в рациональном сочетании.
Расчет оптимального сочетания факторов можно выполнить только на основе знания степени их влияния. Имея модель производственного процесса, несложно определить необходимые объемы производственных ресурсов, т.е. производственные функции дают возможность находить рациональное сочетание факторов, что способствует повышению эффективности использования трудовых, материальных и финансовых ресурсов.
3. Предметом анализа, как известно, являются хозяйственные процессы предприятий, их подразделений и объединений, происходящие под воздействием как объективных, так и субъективных факторов, и результаты их деятельности, характеризующиеся определенной системой показателей. Перед экономическим анализом ставится ряд задач, основные из которых следующие: расчет степени выполнения установленных нормативов и планов, оценка уровня использования производственных ресурсов, вскрытие имеющихся резервов, оптимизация разрабатываемых планов и т. д.
На основе построенных производственных функций производится расчет целого ряда аналитических характеристик. В частности, определяют коэффициент детерминации, среднюю и предельную эффективность факторов, норму взаимозаменяемости ресурсов и другие показатели, которые невозможно получить с помощью традиционных способов и приемов экономического анализа.
4. Особая область использования производственных функций — это прогнозирование и планирование уровня важнейших показате лей производства. Прогнозирование является предварительным этапом разработки плана и обеспечивает в определенной мере научное обоснование концепции экономического развития на плановый период.
Поскольку прогнозирование имеет очень большое политическое, экономическое и научно-техническое значение, к настоящему времени сформировалась специальная наука, которая получила название прогностики.
Сейчас используется ряд методов прогнозирования. Часть из них базируется на построении производственных функций и на экстраполяции показателей во времени. Производственные функции, моделирующие изменение уровня показателей во времени, получили название трендов. Они определяют тенденцию изменения экономических параметров. На основе трендов составляют прогноз динамики важнейших показателей.
Такой методический подход является возможным, поскольку развитие экономических процессов в целом носит почти равномерный характер. Это обстоятельство обусловливает определенную инерционность поведения экономических систем. Согласно законам физики мерой инерции является масса тела. Поэтому, чем крупнее экономическая система, тем она более инерционная. Разумеется, в таких системах выше будет и достоверность уровня прогнозируемых показателей. Но последнее в значительной степени зависит и от времени упреждения прогноза. Чем этот промежуток времени больше, тем ниже достоверность прогноза. На базе спрогнозированных показателей появляется возможность более обоснованно определять плановые параметры на предстоящий период и отдельные последующие годы.
5. Значительную роль производственные функции могут играть в обработке информации. Экономической информацией называют информацию об общественных процессах производства, распределения, обмена и потребления материальных благ. Самые различные формы воплощения экономической информации получили наименование экономических данных.
Процесс обработки информации включает ее хранение, преобразование и передачу. Под преобразованием информации понимают подготовку исходных данных, формирование производных показателей, решение подготовительных задач, группировку, ранжирование, агрегирование, дезагрегирование показателей, сжатие информации и т. д. Сжатие информации достигается путем построения соответствующих производственных функций.
6. Использование производственных функций является также эффективным в целях обоснования нормативов. Внедрение научно обоснованных нормативов — одно из решающих условий повышения производительности труда и эффективности производства.
Производственные функции предоставляют возможность для научно обоснованного определения норм затрат труда и производства продукции в зависимости от сложившихся нормообразующих факторов. Так, если имеется производственная функция, моделирующая производство продукции в зависимости от наличия факторов, то можно рассчитать ее нормативный уровень и уровень достижения норматива.
7. В последние годы, в связи с необходимостью совершенствования экономического механизма хозяйствования, производственные функции начали применять в целях обоснования уровня оплаты труда. Такой подход является закономерным. В решении проблемы стабилизации, а затем и увеличения производства продукции на предприятиях важнейший фактор — это внедрение эффективных систем оплаты труда.
Оплата является действенным экономическим рычагом роста производительности труда, улучшения качества и увеличения объемов производства продукции, снижения ее себестоимости и повышения эффективности производства.
8. Важную роль могут играть производственные функции при оценке результатов хозяйственной деятельности. Подведение итогов работы предприятий и их производственных подразделений, а также целых регионов с учетом круга основных показателей приводит к задаче комплексной оценки результатов хозяйственной деятельности. Комплексная оценка должна представлять собой обобщенную характеристику достигнутых результатов. Для того чтобы такая оценка была действенным орудием хозяйственного управления, ее конструкция не может быть сложной и труднообъяснимой и, самое главное, она должна обеспечивать получение реального, достоверного, практически значимого критерия.
Теоретически следует, казалось бы, оценивать достижения предприятий или их подразделений по одному какому-то показателю, синтезирующему все стороны производственно-финансовой деятельности того или иного объекта. Однако сложность работы предприятий и недостаточный уровень развития экономической науки не позволяют выделить из числа обобщающих результативных показателей какой-либо один в качестве определяющего. Поэтому задача комплексной оценки результатов хозяйственной деятельности предприятий сводится к агрегированию ряда основных показателей с помощью различных методов.
Если имеется ряд результативных показателей и соответствующих производственных факторов, строят функции по каждому из зависимых признаков. На основе полученных производственных функций определяют теоретический уровень результативного показателя. Затем рассчитывают индекс его выполнения. Такие расчеты производятся по всем показателям, которые хотят учесть при подведении итогов. В конце определяют общий индекс с учетом значимости каждого показателя. Этот индекс и является комплексной оценкой результатов хозяйственной деятельности.
Дата добавления: 2015-08-11; просмотров: 1941;
