Парная корреляция и парная линейная регрессия

Простейшим приемом выявления связи между двумя признаками является построение корреляционной таблицы:

Y X	Y1	Y2	...	Yz	Итого	Yi
X1	f11		...	f1z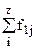
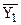
X1	f21		...	f2z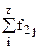
...	...	...	...	...	...	...
Xr	fk1	k2	...	fkz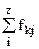
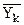
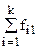
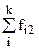
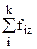
Итого			...		n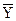
			...			-

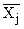
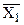
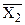
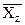
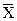
В основу группировки положены два изучаемых во взаимосвязи признака - Х и У. Частоты f_ij показывают количество соответствующих сочетаний Х и У. Если f_ij расположены в таблице беспорядочно, можно говорить об отсутствии связи между переменными. В случае образования какого-либо характерного сочетания f_ij допустимо утверждать о связи между Х и У. При этом, если f_ij концентрируется около одной из двух диагоналей, имеет место прямая или обратная линейная связь.

Наглядным изображением корреляционной таблице служит корреляционное поле. Оно представляет собой график, где на оси абсцисс откладывают значения Х, по оси ординат - У, а точками показывается сочетание Х и У. По расположению точек, их концентрации в определенном направлении можно судить о наличии связи.

В итогах корреляционной таблицы по строкам и столбцам приводятся два распределения - одно по X, другое по У. Рассчитаем для каждого Х_i среднее значение У, т.е. 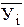, как

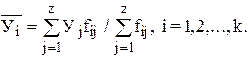
Последовательность точек (X_i, 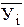) дает график, который иллюстрирует зависимость среднего значения результативного признака У от факторного X, - эмпирическую линию регрессии, наглядно показывающую, как изменяется У по мере изменения X.

По существу, и корреляционная таблица, и корреляционное поле, и эмпирическая линия регрессии предварительно уже характеризуют взаимосвязь, когда выбраны факторный и результативный признаки и требуется сформулировать предположения о форме и направленности связи. В то же время количественная оценка тесноты связи требует дополнительных расчетов.

Постановка задачи построения производственной функции формулируется следующим образом: построить производственную функцию, выражающую зависимость результативного признака от одного или ряда факторов.

Процесс построения производственной функции представляет определенную сложность и поэтому подразделяется на ряд последовательных этапов:

выбор зависимой переменной и отбор производственных факторов, оказывающих на нее влияние;

> подготовка исходной информации;

> идентификация математической модели производственной функции;

> параметризация производственной функции;

> оценка построенной зависимости;

> расчет аналитических характеристик производственных функций.

Выбор зависимой переменной ведется посредством экономического анализа. Такой переменной служит тот показатель, который наиболее полно характеризует исследуемый процесс или явление. Этот результативный признак может выражаться прямым или каким-то косвенным показателем. К числу прямых показателей относятся: качество изделий, выпуск продукции, урожай и т.д. Косвенными, например, при изучении эффективности производства, являются: производительность труда, себестоимость 1 ц продукции и т. д.

Результативные экономические показатели находятся в зависимости от большого числа факторов, и очень важно правильно их отобрать. Если исходить из различных свойств факторов, то их можно подразделить на известные и неизвестные, наблюдаемые и ненаблюдаемые, систематические и случайные, измеримые и неизмеримые, управляемые и неуправляемые, объективные и субъективные, количественные и качественные, существенные и несущественные.

В процессе построения производственных функций отбирают в зависимости от поставленной задачи известные, наблюдаемые, систематические, измеримые, управляемые факторы, которые играют наиболее существенную роль. Не следует стремиться к учету слишком большого числа факторов. Особенно это касается построения первого варианта производственной функции, поскольку это ведет к усложнению ее математической модели, к затруднениям в расчетах и в интерпретации полученных результатов.

После выбора зависимых и влияющих переменных необходимо произвести сбор исходной информации. На практике применяют три основных способа получения исходных данных.

Первый — постановка эксперимента. Этот способ обеспечивает высокую точность информации и является наиболее приемлемым. Но в экономике постановка эксперимента часто очень дорогая и не всегда практически возможна или целесообразна.

Поэтому используют второй способ — это обработка статистических данных. Он менее точный, но более распространенный по сравнению с первым. Третий способ — комбинированный, т.е. часть исходных данных получают экспериментальным путем, а отдельные показатели - по данным статистики.

К исходной информации предъявляется ряд требований. Прежде всего, ее объем должен быть достаточным. Из практики известно, что для построения производственной функции требуется не менее 20-30 наблюдений.

Следующее условие, которому должна соответствовать исходная информация для построения производственных функций, - это достоверность. Впрочем, это требование могло бы занимать первое место, поскольку если информация недостоверна, то она бесполезна и не может служить основанием для построения производственных функций. Поэтому при сборе исходной информации следует вести логический, арифметический и другие виды контроля. Сомнительные данные необходимо перепроверить с тем, чтобы в расчетах использовалась только достоверная информация.

Одно из требований, предъявляемых к информации, - это доступность. Порой случается, что на каком-то предприятии имеется информация, которая необходима другому предприятию или какому-то лицу. Заполучить эту информацию бывает весьма сложно. И часто затруднения возникают не только в вопросах оплаты, Разумеется, это не касается каких-то секретных данных. И тем не менее информация должна быть доступной.

Оперативность - это тоже важное требование, которому должна соответствовать информация, необходимая для построения производственных функций. Какой бы ценной ни была информация, несвоевременное представление сводит на нет ее значимость, так как информация очень быстро устаревает. Поэтому опоздавшие данные превращаются в недоброкачественную и бесполезную информацию.

Большое значение имеет однородность информации. Здесь имеется в виду однородность по месту, времени, технологии и па другим обстоятельствам.

Следует также указать на то, что процесс получения информации для построения статистико-экономических зависимостей не должен быть дорогостоящим. Это касается и хранения, и преобразования, и передачи информации.

Когда исследование ведется по данным всех объектов, то статистическое наблюдение называется сплошным. Однако иногда оно оказывается практически нецелесообразным или неосуществимым, и тогда прибегают к наблюдению какой-то части объектов. Но по его результатам судят об изучаемой зависимости во всей совокупности объектов. Такое наблюдение именуется выборочным. Наблюдаемая часть объектов называется выборкой, а все они - генеральной совокупностью.

Совершенно очевидно, что информация о генеральной совокупности, полученная по данным выборки, характеризуется некоторой погрешностью. Поэтому здесь возникают две задачи. Первая - как организовать выборочное наблюдение, чтобы информация о генеральной совокупности содержала как можно меньше ошибок. Вторая задача касается распространения полученных результатов на генеральную совокупность и их оценки.

Моделирование исследуемых зависимостей. После выбора факторных признаков и зависимых показателей, а также подготовки исходной информации ведется идентификация математической модели производственной функции, т. е. производится выбор соответствующего математического уравнения.

Этот этап построения производственных функций является весьма ответственным, поскольку если вид модели исследуемой связи установлен неверно, то все последующие расчеты не будут иметь какого-либо значения.

Наиболее простым из них является графический (визуальный) способ. Его сущность сводится к тому, что выбор вида производственной функции ведется на основе графика, построенного по данным исходной информации.

В случае, когда характер графика исходных данных не позволяет решить вопрос о виде существующей связи, используют скользящие средние. При этом исходные данные разбивают на небольшие, например, трех- или пятилетние периоды. Причем каждый следующий период получают путем сдвига предыдущего на один год. Продолжительность периодов рекомендуется выбирать в прямой зависимости от колеблемости исходных данных. Если построить график по средним данным за ряд таких последовательных периодов, то он будет иметь более выровненный характер.

Следующим способом идентификации модели статистико-экономических зависимостей является экономический анализ связи между результативными и факторными показателями. Например, если необходимо установить вид функции, моделирующей себестоимость единицы продукта от производительности агрегата или в целом технологического процесса, то явно целесообразна функция

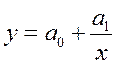
где a₀, a₁ - параметры функции;

у и х — соответственно себестоимость и производительность.

Нередко эффективным является способ аналогии. Он применим в тех случаях, когда возникает необходимость выбора математической модели производственной функции в зависимостях, аналогичных тем, которые уже рассматривались. При этом можно воспользоваться ранее избранной моделью.

Выбирая вид производственной функции, иногда прибегают к составлению группировочных комбинационных таблиц. Сгруппированные по факторному признаку данные могут подсказать, какое уравнение целесообразно использовать как модель исследуемой зависимости. В том случае, когда равномерное увеличение фактора вызывает примерно равномерное изменение зависимого признака, моделью целесообразно взять уравнение прямой. Если же при указанном характере роста факторного признака идет равномерно ускоренное изменение результативного показателя, то в качестве модели следует использовать параболу второго порядка.

В последние годы все шире находит применение способ «перебора» моделей производственных функций на ЭВМ. Наиболее приемлемая модель определяется по уровню статистических характеристик всех видов производственных функций, которые включены в специально разработанную программу. Разумеется, этот способ идентификации математической модели производственной функции в определенной мере расточительный, но результативный.

В особо сложных случаях только использование всего комплекса известных способов и проверка различных гипотез могут привести к получению практически приемлемой модели. Этап идентификации модели производственной функции является весьма ответственным и заслуживает особого внимания.

Способы расчета параметров производственных функций. После выбора зависимой переменной и факторных признаков, сбора и подготовки информации, идентификации модели следует четвертый этап — параметризация производственных функций. На этом этапе рассчитываются параметры исследуемой зависимости при помощи ряда способов.

Наибольшее распространение получил способ наименьших квадратов, который был предложен немецким ученым К. Ф. Гауссом и французскими математиками А. М. Лежандром и П. С. Лапласом в первой четверти XIX в. Способ предназначался для обработки и оценки ошибок. Но он оказался настолько удачным, что его используют и сейчас, хотя ив несколько других целях.

Сущность этого способа заключается в том, что величина параметров производственной функции должна быть такой, чтобы достигался минимум суммы квадратов отклонений между теоретическими (у_х) и фактическими (у) значениями зависимого показателя. Если моделью исследуемой зависимости выбрано уравнение прямой

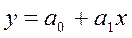, то а₀ и а₁ необходимо рассчитать так, чтобы

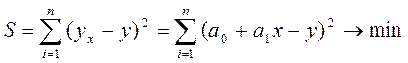
Поскольку х и у заданы, то S является величиной, зависимой от определяемых параметров а₀ и а_х:

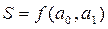
Так как производная функции в точке минимума равна нулю, на основе можно записать:

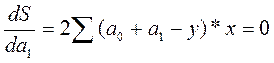
После преобразований эта система уравнений принимает вид:

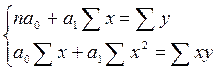
Системы данного вида получили наименование нормальных.

Системы нормальных уравнений решаются различными способами, чаще всего с помощью определителей. В результате получают следующие выражения:

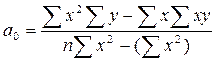
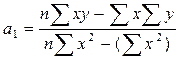
Оценка построенных производственных функций. После получения производственных функций производится их оценка. Когда в качестве исходной информации использовалась вся генеральная совокупность, а не данные выборки, то оценку осуществляют по так называемым показателям тесноты связи. Если построена линейная однофакторная зависимость, то для ее оценки вычисляют коэффициент парной линейной корреляции:

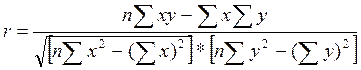
где n - число наблюдений.

Коэффициент парной линейной корреляции находится в границах от —1 до +1. Когда он равен —1, связь является функциональной, но обратной, т.е. с увеличением факторного признака зависимый показатель снижается и наоборот. Если же коэффициент парной линейной корреляции составляет +1, связь тоже функциональная, но прямая. Коэффициент парной линейной корреляции может быть равным нулю. В этом случае какая-либо связь между факторным и зависимым признаками отсутствует. Коэффициент парной линейной корреляции не изменяется при смене мест факторного и зависимого признаков, т. е. r_xy=r_yx.

Аналитические характеристики производственных функций и их экономическая трактовка. Построенные производственные функции в дальнейшем необходимо использовать в целях углубленного исследования экономических явлений и процессов. На основе полученных статистико-экономических зависимостей представляется возможность рассчитать ряд аналитических характеристик, которые нельзя получить с помощью традиционных методов. К числу важнейших аналитических характеристик относятся: коэффициент детерминации, средняя и предельная эффективность ресурса, коэффициент эластичности, норма взаимозаменяемости факторов, и др.

Коэффициент детерминации характеризует удельный вес факторного признака или признаков в общей вариации зависимого показателя. Аналогично с показателями тесноты связи различают коэффициент парной (однофакторной) детерминации и коэффициент множественной детерминации. Коэффициент детерминации (К_д) рассчитывают как квадрат соответствующего показателя тесноты связи. Нередко детерминацию исчисляют в процентах.

К_д = 100 г²

Это значит, что уровень показателя обусловливает К_д всех колебаний, а остальные % объясняются влиянием других, не учтенных в этом исследовании факторов.

Когда детерминация меньше 10 %, она считается слабой, если же она находится в пределах 10 — 50 % — средней, свыше 50 % - сильной и при 100 % - полной.

Средняя эффективность ресурса определяется путем деления соответствующей производственной функции на объем использованного ресурса. Эффективность измеряется в единицах результативного показателя в расчете на единицу ресурса. Среднюю эффективность ресурса необходимо рассчитывать как в анализе, так и в прогнозировании и планировании производства.

Если моделью статистико-экономической зависимости служит уравнение прямой у = а₀ + а₁х, средняя эффективность будет равна:

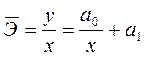
Как видно, средняя эффективность ресурса в этом случае изменяется по гиперболическому закону. Чем больше факторный признак х, тем средняя его эффективность ближе к а₁.

Предельная эффективность ресурса измеряется в единицах зависимого показателя в расчете на единицу факторного признака.

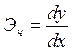
В случае парной линейной зависимости у = а₀ + а₁х предельная эффективность ресурса составляет

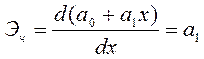
Иными словами, является постоянной величиной и равной коэффициенту регрессии a₁,. По своему содержанию она представляет собой изменение зависимого показателя при увеличении факторного признака на единицу.

Следующая аналитическая характеристика производственных функций - эластичность. Ее рассчитывают путем умножения предельной эффективности ресурса на соотношение значений фактора и зависимого признака:

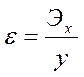
Если в формулу подставить средние уровни факторного и результативного показателей, то эластичность будет именоваться средней.

При линейной производственной функции у = а_о+а₁х эластичность составляет

Она показывает, на сколько процентов изменяется результативный показатель у с отклонением факторного признака х на 1%, т. е. представляет собой соотношение темпов прироста у их. Знание уровня и сравнение эластичности различных ресурсов позволяет планировать их более рациональное использование.