Электромагнитные поля, созданные постоянным током.
При наличии постоянного тока электрические и магнитные поля нельзя считать независимыми, а созданные этим током поля называются стационарным электромагнитным полем. В этом случае система уравнений Максвелла имеет вид:
rot Н = j ; divВ = 0; B = 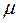 аH; Iпр =ω E; (5.17,а )
аH; Iпр =ω E; (5.17,а )
rot Е = 0; divD = 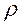 ; D =
; D =  аE. (5.17,б)
аE. (5.17,б)
В заключении раздела необходимо отметить, что мы рассмотрели четыре уравнения Максвелла (5.13) и материальные уравнения (5.14), которые применяют в электродинамике. Однако в случае гармонических электромагнитных полей система этих уравнений для комплексных амплитуд Е и Н сводится только к двум первым уравнениям (5.9) и (5.11), а именно:
 rot H = iω
rot H = iω  аE, (5.18)
аE, (5.18)
rot E = -iω 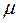 аH.
аH.
При решении конкретных задач, кроме системы уравнений Максвелла, необходимо использовать граничные условия, позволяющие рассматривать поведение векторов электромагнитного поля на границе раздела сред с различными электрофизическими параметрами, где амплитуды векторов поля могут меняться скачком. Эта необходимость вызвана тем, что операция дифференцирования в точках раздела сред не имеет места.
Соотношения, показывающие связь между значениями векторов электромагнитного поля в разных средах у поверхности раздела, называются граничными условиями. Используя граничные условия на поверхности, ограничивающей объем РЭС, с помощью уравнений Максвелла можно рассчитать поле внутри его объема, а затем, зная электрические характеристики используемых материалов, определить основные электрические характеристики электромагнитного поля.
На поверхности раздела двух изотропных сред с параметрами и 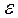 а1,
а1, 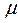 а1 и
а1 и 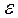 а2,
а2, 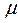 а2 при поверхностно распределенном заряде вдоль поверхности граничные условия нормальных компонент вектора Е /18,19/:
а2 при поверхностно распределенном заряде вдоль поверхности граничные условия нормальных компонент вектора Е /18,19/:
 а1 Е1n -
а1 Е1n -  а2 Е2n = σs
а2 Е2n = σs  S =
S =  s, (5.19)
s, (5.19)
где σs - поверхностная плотность электрического заряда;  S - площадь поверхности раздела двух сред.
S - площадь поверхности раздела двух сред.
Если на границе раздела нет поверхностных зарядов, то граничные условия можно представить в виде:
 а1Е1n =
а1Е1n =  а2Е2n ;
а2Е2n ; 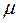 а1H1n =
а1H1n = 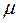 а2H2n. (5.20)
а2H2n. (5.20)
Для тангенциальных составляющих (касательных к поверхности) векторов Е и Н граничные условия имеют вид:
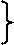 |
Е1  = Е2
= Е2  ;
;
Н1  = Н2
= Н2  (5.21)
(5.21)
т.е. эти составляющие на границе раздела непрерывны.
Внутри идеального проводника (Е=Iпр;σ=0), т.е. поле Е отсутствует (Е = 0). В этом случае из второго уравнения Максвелла следует, что 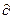 В/
В/ 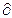 t = 0 и В = const, и внутри проводника существует только постоянная составляющая магнитного поля (Н1n = 0).
t = 0 и В = const, и внутри проводника существует только постоянная составляющая магнитного поля (Н1n = 0).
Граничные условия для идеального проводника принимаю вид:
Е1n =  s/
s/ 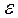 а1 ; Е1
а1 ; Е1  = 0 ; (5.22)
= 0 ; (5.22)
Н1  = Js ; H1n = 0, (5.23)
= Js ; H1n = 0, (5.23)
т.е. тангенциальная составляющая вектора напряженности магнитного поля равна по величине плотности поверхностного тока Js и направлена перпендикулярно направлению тока.
Дата добавления: 2015-08-11; просмотров: 1450;
