Нелинейное программирование в Excel

Задачи нелинейного программирования в Excel решаются с помощью знакомых уже опций Сервис – Поиск решения. Однако в диалоговом окне Параметры поиска решенияне надо устанавливать флажок Линейная модель.

Рассмотрим пример.

Минимизировать функцию f(x)=(х₁-2)⁴+(х₁-2х₂)² при ограничениях х_1,2>0

Введем в ячейки А3 и В3 начальные значения искомых переменных (рис.1.), в ячейку С3 – целевую функцию через адреса ячеек, в которых присвоены начальные значения искомых переменных, в ячейки D3 и E3 производные (для контроля).

Рис. 1. Ввод начальных значений и формул

Тогда получим вид листа, приведенный на рис.2.

Рис. 2. Вид листа после ввода формул

Далее из меню Сервис необходимо вызвать диалоговое окно Поиск решения (рис.3.). В нем в поле Установить целевую ячейку ввести адрес ячейки, где записана целевая функция, далее установить флажок по цели решения – на максимум или минимум.

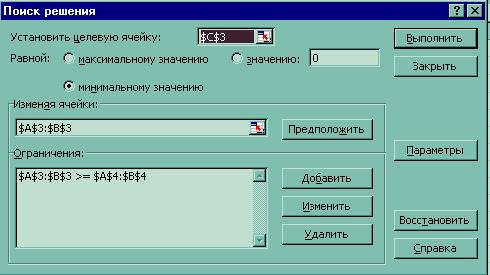
Рис. 3. Диалоговое окно Поиск решения

В поле области Изменяя ячейки ввести адрес ячеек, где установлены начальные значения переменных, и в поле области Ограничения ввести ограничения модели. Нажать кнопку Параметры.В открывшемся диалоговом окне Параметры поиска решения (рис. 4.) снять флажок Линейная модель, если он установлен.

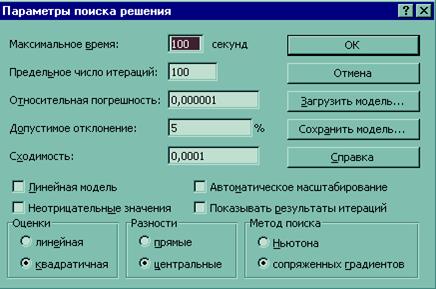
Рис. 4. Диалоговое окно Параметры поиска решения

Выбрать метод решения. В Excel существует два метода – квазиньютоновский метод и метод сопряженных градиентов. Под параметром Разности понимается метод численного дифференцирования, аппроксимация производных с помощью центральных разностей предпочтительней. Под командой Оценка понимается характер шага метода. Смысл остальных параметров очевиден.

Далее после нажатия кнопок ОК и Выполнить получим результат минимизации функции, приведенный на рис. 5.

Рис. 5. Результат минимизации функции

При желании увеличить точность, можно уменьшив относительную погрешность и сходимость (рис. 6.), и получить результат как на рис. 7.

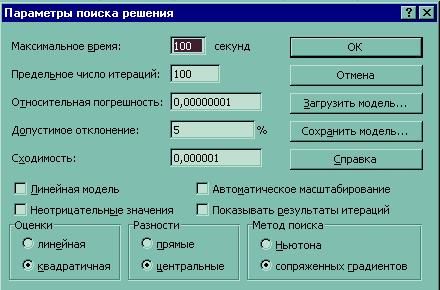
Рис. 6. Окно Параметры поиска решения с меньшей относительной погрешностью и сходимостью

Рис. 7. Окно Результат вычислений после уменьшения относительной погрешности и сходимости

Рассмотрим другой пример – функцию Розенброка, часто используемую как тестовую. Необходимо минимизировать функцию f(x)=100(у-х²)²+(1-х)²

Функция Розенброка имеет минимум в точке х=1, у=1. Введем начальные значения и целевую функцию, как показано на рис. 8.

Рис. 8. Ввод начальных значений и целевой функции

После запуска решающего блока получим результат, представленный на рис. 9.

Рис. 9. Результат после первого запуска

Не меняя погрешности и сходимости, сделаем еще запуск решающего блока. Получим удовлетворительный результат, представленный на рис. 10.

Рис. 10. Результат минимизации функции Розенброка

Этого результата можно добиться, изменяя значения погрешности и сходимости.