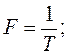Частотный спектр импульсного колебания
Большинство импульсных колебаний, встречающихся на практике, представляют собой периодические процессы. Периодическим процессом называется такой процесс, который повторяется во времени через определенные промежутки времени.  Этот процесс можно описать следующей функцией времени:
Этот процесс можно описать следующей функцией времени:
f ( t ) = f ( t + nT ),
где T – период повторения процесса;
n – любое целое число.
Основная частота F повторяющегося процесса связана с периодом его повторения следующим соотношением:
|
Периодическая последовательность электрических импульсов может быть представлена в виде суммы бесконечного множества синусоидальных составляющих (гармоник) с частотами, кратными основной частоте:
– частота первой гармоники: F1 = F;
– частота второй гармоники: F2 = 2F;
– частота третьей гармоники: F3 = 3F и т. д.
Совокупность синусоидальных составляющих импульсных колебаний образует частотный спектр этих колебаний.
Теоретически частотный спектр прямоугольных видеоимпульсов простирается до бесконечности, поэтому для передачи и приема таких сигналов без искажений требуется бесконечно широкий спектр частот. Если ограничиться передачей какого-либо конечного числа гармоник, то импульсы будут приниматься с некоторыми искажениями.
Частотный спектр последовательности прямоугольных видеоимпульсов представлен на рис. 3.6.4.


Рис. 3.6.4. Частотный спектр последовательности видеоимпульсов
Рассматривая частотный спектр, приведенный на рисунке 3.6.4, можно сделать следующие выводы:
a) Спектр видеоимпульса дискретный. Он состоит из спектральных линий с частотами F, 2F, 3F, 4F и т. д.
Интервал между спектральными линиями определяются периодом повторения импульсов Т:

Если период Ти увеличить в два раза, то первоначальные линии спектра сохраняют свою величину и положение, но между ними появляются новые линии. Дальнейшее увеличение периода приведет к тому, что густота спектральных линий возрастает, и, если период Ти стремится к бесконечности, то интервал между спектральными линиями неограниченно сокращается. Тогда вместо совокупности дискретных линий спектр будет изображаться непрерывной кривой. Такой спектр называется сплошным (рис. 3.6.5).


Рис. 3.6.5. Сплошной частотный спектр одиночного видеоимпульса
b) Огибающая спектра амплитуд убывает с ростом частоты и периодически меняет свой знак.

c) Амплитуды гармоник, имеющих частоты , , и т. д. равны нулю.
d) Наибольшую амплитуду имеют гармоники, расположенные в интервале между основной частотой, равной частоте повторения импульсов Fи, и частотой первого нуля, равной 1/t . Поэтому в большинстве случаев считается, что полоса частот прямоугольного видеоимпульса заключена в пределах от fmin = Fи до fmax = 1/tи.
Частотный спектр радиоимпульсов в 2 раза шире, чем спектр видеоимпульсов (рис. 3.6.6).


Рис. 3.6.6. Частотный спектр радиоимпульсов
Дата добавления: 2015-08-08; просмотров: 694;