Упругие деформации грунтов и методы их определения.

Грунты, представляющие собой сложные дисперсные природные образования, можно рассматривать как упругие тела лишь при определенных условиях.

При действии местной нагрузки (большей структурной прочности грунта) и однократной нагрузке и разгрузке в грунте будут наблюдаться как остаточные, так и упругие деформации, причем остаточные деформации часто будут во много раз превосходить по величине другие деформации; при многократном повторении нагрузки и разгрузки грунт постепенно будет приходить в упруго-уплотненное состояние, характеризующееся постоянством (для данных условий загружения) его упругих свойств.

Если увеличить нагрузку на грунт, сверх той, при которой грунт принял упруго-уплотненное состояние, то в грунте вновь возникнут остаточные деформации, которые при достаточном большом числе циклов загрузки и разгрузки, приведут грунт к новому упруго-уплотненному состоянию, но с большим модулем упругости (меньшим наклоном к оси давлений кривой деформации грунта при разгрузке). Такое увеличение ступеней нагрузки можно производить до тех пор, пока не будет превзойден предел фазы уплотнения грунта и не наступит фаза развития сдвигов.

Если грунт обладает связностью, то до нагрузки, не разрушающей структурных связей, и при малых перемещениях частиц и структурных элементов грунтов, он будет вести себя как упругое тело на что указывает непосредственный опыт передачи через грунты упругих колебаний: вибраций, сейсмических волн, сотрясений и др., если же при циклической нагрузке структурные связи будут разрушены, то грунт только после соответствующих циклов нагрузки и разгрузки придет в новое упругоуплотненное состояние.

Из методов определения упругих деформаций грунтов следует различать метод общих упругих деформаций, когда учитываются упругие перемещения не только точек, лежащих под нагруженной поверхностью, но и точек лежащих вне её, метод местных упругих деформаций, когда учитываются лишь деформации непосредственно в месте приложения нагрузки, а общие упругие деформации массива грунта не рассматриваются; некоторые обобщенные методы, учитывающие как общие восстанавливающие деформации, включая упругие, так и местные, но остаточные деформации.

Метод общих упругих деформаций базируется на строгих решениях теории упругости для упругого полупространства и для упругого слоя ограниченной конечной толщины, лежащего на несжимаемом основании.

Исходной зависимостью при определении общих упругих деформаций полупространства является формула Буссинеска для вертикальных перемещений точек, лежащих на ограничивающей полупространство плоскости (z=0) при действии на полупространство сосредоточенной силы Р – ω_z

ω_z=Р/(π*с*R),

где с- коэффициент упругого полупространства

с=Е/(1-μ²)

Е- модуль упругости следует заменить на модуль общей деформации Е_о, а коэффициент Пуассона μ- на коэффициент общей относительной поперечной деформации μ_о.

При действии на ограничивающую упругое полупространство плоскость местной равномерно распределенной по площадке F нагрузки осадки любой точки определяются путем интегрирования выражения для вертикальных перемещений упругого полупространства от сосредоточенной силы рdξdη.

S_упр= ω’/c*p√F, где

S_упр- осадка упругого полупространства,

ω’- интегральный коэффициент (табулируемый),

с- коэффициент упругого полупространства

Р- удельное давление на грунт

F- плоскость местной равномерно распределенной по площадке нагрузки

Это выражение показывает, что осадки однородного упругого (или линейно деформируемого) полупространства прямо пропорциональны удельному давлению на грунт Р и корню квадратному из площади √F (ω’/c- коэффициент пропорциональности теоретический).

Важно отметить, что опыты в натуре по изучению осадок грунтовых оснований для площадей от 0,5 до 15м² на однородном заиленном песке мощностью около 12м, а также опыты на массовидных однородных суглинках с площадями от 0,25 до 8м² в пределах линейной связи между давлением и осадкой дают следующую эмпирическую зависимость

S=A*p*√F

где А- коэффициент пропорциональности (опытный), отличный от теоретического ω’/c.

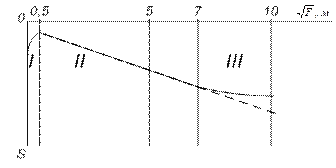
Рис. 3.1. Зависимость осадки природных грунтов от размеров площади загрузки (по Цытовичу стр.66)

Однако зависимость осадки от величины площади загрузки в природных условиях при большом диапазоне изменения площадей выражается более сложной зависимостью, устанавливаемой на обобщенной кривой средних результатов многочисленных опытов по изучению осадки грунтовых оснований средней уплотненности при одинаковом давлении на грунт, но разной величине площади загрузки.

На этой кривой различаются три области:

Область I – малых площадей загрузки ( ̴ 0,25м²), где грунты находятся в фазе сдвигов, наблюдается уменьшение осадки с увеличением площади; область II- при площадях от 0,25-0,50 до 25-50м², где осадки грунтов строго пропорциональны √F и соответствуют при средних давлениях фазе уплотнения, т.е. весьма близки к теоретическим; область III- для площадей >25-50м², где осадки меньше теоретических, вследствие возрастания модуля упругости (уменьшения деформируемости) грунтов с глубиной. Общепринятая формула расчета зависимости осадки от величины площади загрузки и действующего внешнего давления получим, введя отношение длины к ширине сторон прямоугольной площади загрузки а=l/b (а следовательно l=a*b и F=a*b²) и обозначив через ω величину ω’ √а

S_упр= (ω*р*b*(l-μ²))/Е,

где S_упр- осадка упругого полупространства;

ω- коэффициент формы площади подошвы и жесткости фундамента (табулированный);

р- удельное давление на грунт;

b- ширина прямоугольной площади подошвы или диаметр круглой;

Е,μ- модули упругости (деформируемости) полупространства;

l- длина прямоугольной площади подошвы.

Эту формулу используют обычно и для опытного определения по результатам полевой пробной нагрузки (площадкой в 5000см²) модуля общей деформации грунта Е_о кгс/см² (Н/м²).

Е_о= (ω*p*b*(l-μ_o²))/S

где S- общая осадка штампа, но в пределах линейной зависимости между осадками S и давлением Р;

μ_o- коэффициент относительной поперечной деформации, равной:

для глин и суглинков: твердых и полутвердых 0,1÷0,15

тугопластичных 0,20÷0,25

пластичных и текучепластичных 0,30÷0,40

текучих 0,45÷0,50

для супесей 0,15÷0,30

для песков 0,20÷0,25

Метод местных упругих деформаций учитывает лишь упругие деформации непосредственно в месте приложения нагрузки и базируется на гипотезе Фусса-Ванклера, согласно которой давление в данной точке прямо пропорционально лишь местной осадке грунта в этой точке, т.е.

р=с_zz

где р- удельное давление, кгс/см²;

с_z- коэффициент упругости основания (коэффициент постели), кгс/см² (Н/м²);

z- вертикальное упругое перемещение – местная упругая осадка, см (м).

Отсюда z=h/c_z

Уравнение показывает, что упругая осадка грунта будет иметь место лишь в месте приложения нагрузки; в том же месте где р=0, вертикальное упругое перемещение (местная упругая осадка) z=0.

Метод местных упругих деформаций полностью применим для конструкций, имеющих постоянную площадь подошвы и испытывающих одинаковый диапазон изменения внешних давлений (например железнодорожных шпал).

Для фундаментов сооружений занимающих большую площадь в плане применять метод местных упругих деформаций можно лишь с известным приближением при толщине слоя сжимаемого грунта меньше ширины полосы, т.е. для очень малых толщин слоя сжимаемого грунта.

Обобщенные методы определения деформаций грунтов учитывают как общие, так местные упругие деформации грунтов. К ним относятся метод двухпараметрового упругого основания, согласно которому грунтовое основание характеризуется коэффициентов постели с₁, кгс/см²(Н/м²) и коэффициентом местного упругого сдвига с₂ кгс/см (Н/м), и метод структурно-восстанавливающихся деформаций, учитывающий восстанавливающиеся деформации (упругие и адсорбционные), остаточные (структурные).

В последнем методе восстанавливающиеся деформации принимаются за линейно-деформируемые и характеризуются коэффициентом упругого полупространства

с_в=(l-μ_b²)/E_b

а структурные деформации определяются по теории размерностей, исходя из степенной зависимости

р=А*(S_ост/D)ⁿ,

где р- внешнее удельное давление (нагрузка), кгс/см² (Н/м²);

А- число твердости, кгс/см² (Н/м²);

S_ост- остаточная деформация, см (м);

D- диаметр круглой площади загрузки см (м);

n- степень упрочнения.

Величина полной осадки при круглой площади загрузки по этому методу определяется выражением

S_o/D=π/4*c_b*p+ⁿ√(p/a),

а осадка точек поверхности грунта вне загруженной площадки.

S_r=D/2*c_b*arcsin(D/2r),

где r- расстояние от рассматриваемой точки на поверхности грунта до центра круглой площадки.

Применяется при расчете нежестких дорожных одежд.