Распределение напряжений в основании сооружений от сосредоточенной силы.

Существует два решения задачи для определения напряжений в линейно-деформируемом основании: Буссинеска и Миндлина.

Решение Буссинеска. При приложении вертикальной сосредоточенной силы к поверхности линейно-деформированного полупространства, ограниченного горизонтальной плоскостью и имеющего безграничную протяженность в остальных направлениях, в соответствии с решением Буссинеска в любой произвольной точке М(рис) полупространства

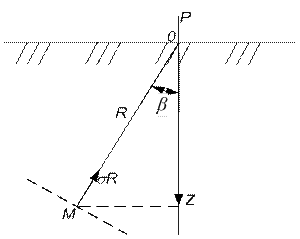
Рис. 4.2 Исходная расчетная схема задачи Буссинеска

Радиальное напряжение Ϭ_R, возникающее от нагрузки Р и действующее по площадке, перпендикулярной радиусу, проведенному из точки приложения нагрузки О через точку М выражается формулой

Ϭ_R=В*cosα/R² (2.1)

Очевидно, что с увеличением отклонения радиуса-вектора R от линии действия силы Р интенсивность напряжения Ϭ_R уменьшается и при β=90^о становится равной нулю. Функция cosβ отражает это обстоятельство. Значение коэффициента В определяется из условий статического равновесия. При этом

В=3Р/2π (2.2)

Подстановка значения этого коэффициента в формулу Ϭ_R приводит к

Ϭ_R=3*Р*cosβ/2*π*R² (2.3)

Проекция Ϭ_R на площадке через М (рис 3.3) приводит к ряду выражений

Ϭ_z=3*Р_z³/2*π*R⁵ (2.4)

τ_zy=3*P_z³/2*π*R⁵ (2.5)

τ_zx=3*P_x³/2*π*R⁵ (2.6)

С учетом обозначений на рис. 3.3

Ϭ_z=К*Р/Z² (2.7)

Где К- справочный коэффициент, зависящий от отношения r/z; z – глубина от дневной поверхности.

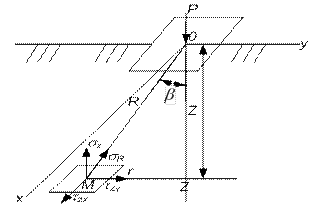
Рис. 4.3. Разложение Ϭ_R на горизонтальной плоскости в точке М в декартовой системе координат

r – расстояние по горизонтали от линии действия сосредоточенной силы до точки М

Решение Миндлина. Наряду с получившей широкое распространение в расчетах естественных оснований формулой (2.4) при анализе глубинных испытаний грунтов пробными нагрузками и исследовании работы свай используется решение Р Миндлина для определения Ϭ_z- напряжений от действия сосредоточенной силы Р, приложенной на глубине h от поверхности линейно-деформированного полупространства.

В упрощенном виде Ϭ_z определяется по формуле: Ϭ_z=К_h*P/h², (2.8)

Где К_h – безразмерный коэффициент, определяемый в зависимости от приведенных координат z/h и r/h;

z – глубина расположения точки М;

h – глубина приложения сосредоточенной силы;

r – расстояние (по горизонтали) от линии действия сосредоточенной силы до точки М;

Рис. 4.4 Схема к определению Ϭ_R в основании от сосредоточенной силы, приложенной внутри линейно-деформируемого полупространства.