Сила упругости

В деформированном теле всегда возникает внутренняя сила упругости, направленная противоположно смещению и пропорциональная этому смещению (закон Гука).

Направим ось координат вдоль пружины (рис. 1.4). Тогда закон Гука имеет вид:

F_упр=-kx. (1.10)

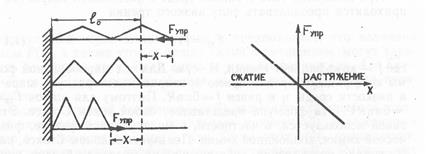
Рис. 1.4. Зависимость силы упругости от смещения пружины

В о п р о с: напишите формулу для величины силы упругости.

При растяжении пружины сила упругости направлена влево против направления оси координат х и поэтому считается отрицательной (рис. 1.4). При сжатии сила упругости направлена по оси х, поэтому F_ynp—положительная величина.

Коэффициент упругости k не зависит от смещения пружины х. Коэффициент упругости измеряется в Н/м и характеризует упругие свойства данной пружины; он зависит от упругих свойств материала и от размеров деформируемого тела. Чем меньше витков имеет пружина, тем менее она податлива и, следовательно, тем больше коэффициент упругости. Вообще, чем короче и толще тело, тем труднее его деформировать. Поэтому k = ES/l₀, где S и l₀ — площадь и длина тела в недеформированном состоянии. Величина Е называется модулем Юнга и характеризует материал, из которого сделано упругое тело. Модуль Юнга измеряется в единицах давления — паскалях (Па =Н/м²). Численные значения модуля Юнга для разных материалов приводятся в справочниках. Итак, закон Гука можно записать в виде: . Часто вместо внутренней силы упругости рассматривают приложенную силу . 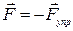Тогда 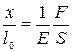. В этом случае закон Гука формулируется таким образом: относительное смещение упругого тела пропорционально приложенному давлению. В этой форме закон Гука обычно используют механики-технологи.

Упругие силы часто встречаются в природе. Например, силы взаимодействия между атомами или молекулами приближенно можно считать упругими вблизи положения равновесия.

В о п р о с: нарисуйте зависимость коэффициента упругости k от смещения х для «мягкой» и «жесткой» пружины.