Сила гравитации

СИЛА

Основу механики составляет второй закон Ньютона. При математической записи закона справа пишут причину, а слева — следствие. Причиной является сила, а следствием сил — ускорение. Поэтому второй закон записывается так:

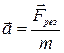(1.1)

Ускорение тела пропорционально результирующей силе, действующей на тело, и обратно пропорционально массе тела. Направлено ускорение по направлению результирующей силы. Результирующая сила равна векторной сумме всех сил, действующих на тело: .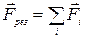

Реальные силы 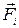характеризуют меру взаимодействия двух тел. В дальнейшем мы будем рассматривать несколько видов взаимодействий — гравитационное, электрическое, молекулярное. Каждому виду взаимодействий соответствует своя сила. Если взаимодействий нет, то нет и сил. Поэтому, прежде всего необходимо выяснить, какие тела взаимодействуют друг с другом.

Сила гравитации

Тело брошено и летит над Землей (рис. 1.1). Имеется только

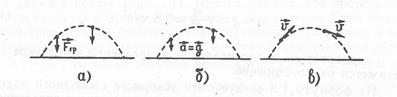
Рис. 1.1. Силы, действующие на брошенный камень (а), ускорение камня (б) и его скорость (в)

взаимодействие тела с Землей, которое характеризуется гравитационной силой притяжения (тяготения). По закону всемирного тяготения гравитационная сила направлена к центру Земли и равна

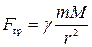, (1.2)

где М - масса Земли, т — масса тела, r — расстояние от центра Земли до тела, γ — гравитационная постоянная. Других взаимодействий нет, поэтому нет и других сил.

Чтобы найти ускорение камня, гравитационную силу из формулы 1.2 подставляют в формулу 1.1 второго закона Ньютона. Очевидно, ускорение камня всегда направлено вниз (рис. 1,1,б). В то же время скорость летящего камня меняется и в каждой точке траектории направлена по касательной к этой траектории (рис. 1.1, в).

Второй закон Ньютона связывает векторные величины — ускорение а и результирующую силу 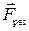. Любой вектор задается величиной (модулем) и направлением. Можно задать вектор тремя проекциями на координатные оси, то есть тремя числами. При этом выбор осей определяется удобством. На рис. 1.1 ось х можно направить вниз. Тогда проекции ускорения будут равны а_х, 0, 0. Если же ось х направить вверх, то проекции ускорения станут равны -а_х,0,0. В дальнейшем мы будем выбирать направление оси х так, чтобы оно совпадало по направлению с ускорением и для простоты будем писать не величину а_х, а просто а. Итак, ускорение, создаваемое гравитационной силой, равно

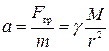(1.3)

Для тел, находящихся вблизи поверхности Земли, r » R (радиус Земли R = 6400 км), поэтому

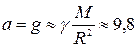м/с² (1.4)

Следовательно, в вертикальном направлении брошенное тело движется равноускоренно.

Из формулы 1.3 следует, что ускорение свободного падения не зависит от массы летящего (падающего) тела и определяется только массой планеты М и удаленностью тела от центра планеты r. Чем дальше от центра планеты находится тело, тем меньше ускорение свободного падения.

По формуле 1.4 можно рассчитать ускорение, с которым падают тела на других планетах. Например, для Луны R_л»R/4, 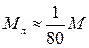и, соответственно, » 2 м/с².

Когда в 1798 г. английский физик Генри Кавендиш экспериментально определил величину гравитационной постоянной γ»6,67·10^-11 H·м²/кг², то говорили, что он «взвесил Землю». Действительно, зная гравитационную постоянную и радиус Земли, из формулы 1.4 находим М=9,8·(6,4·10⁶)²/6,67· 10^-11»6,02·10²⁴ кг.

Отметим, что формула 1.2 справедлива только для тел шаро­образной формы и для «точечных тел», размеры которых гораздо меньше расстояния между ними.

Если тела неправильной формы и находятся близко друг к дру­гу, то сила гравитационного взаимодействия будет зависеть от взаимной ориентации этих тел.