Звуковые волны в газе. Эффект Доплера.
В газах могут распространяться только продольные волны. Звуковые волны в воздухе имеют частоты примерно от 16 Гц до 20 кГц. Волны с 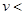 16 Гц называют инфразвуком, а с
16 Гц называют инфразвуком, а с 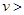 20 кГц – ультразвуком.
20 кГц – ультразвуком.
Интенсивность звука 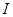 - средняя по величине энергия, переносимая звуковой волной через единичную площадку, перпендикулярную к направлению распространения волны в единицу времени.
- средняя по величине энергия, переносимая звуковой волной через единичную площадку, перпендикулярную к направлению распространения волны в единицу времени. 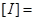 1 Вт/м2 .
1 Вт/м2 .
Порог слышимости: 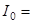 10-12 Вт/м2. Уровень громкости:
10-12 Вт/м2. Уровень громкости: 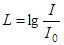 ,
, 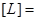 1 Белл (Б). Обычно измеряют уровень громкости в децибелах: 1 дБ = 0.1Б. Для нормальной речи уровень громкости составляет порядка 60 дБ. Двигатель самолета на расстоянии 5 м дает громкость около 120 дБ.
1 Белл (Б). Обычно измеряют уровень громкости в децибелах: 1 дБ = 0.1Б. Для нормальной речи уровень громкости составляет порядка 60 дБ. Двигатель самолета на расстоянии 5 м дает громкость около 120 дБ.
Скорость звука в газе.
Значение скорости звука в газе определяется упругими свойствами этого газа. Скорость звука можно вычислить, используя выражение для скорости волны в упругом стержне 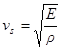 , полученное в лекции 18. Вместо
, полученное в лекции 18. Вместо 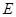 в него нужно подставить значение “модуля Юнга”
в него нужно подставить значение “модуля Юнга” 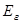 для газа, вытекающее из связи между изменениями его давления и объема. При распространении звуковой волны в газе области сгущения и разрежения не успевают обме-ниваться теплом. Такие процессы в термодинамике называются адиабатическими. Они будут подробно изучаться в курсе молекулярной физики. Здесь мы просто воспользуемся уравнением Пуассона для адиабатического процесса
для газа, вытекающее из связи между изменениями его давления и объема. При распространении звуковой волны в газе области сгущения и разрежения не успевают обме-ниваться теплом. Такие процессы в термодинамике называются адиабатическими. Они будут подробно изучаться в курсе молекулярной физики. Здесь мы просто воспользуемся уравнением Пуассона для адиабатического процесса
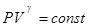 , (1)
, (1)
где 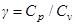 ,
, 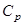 и
и 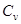 - соответственно теплоемкости газа при постоянном давлении и постоянном объеме.
- соответственно теплоемкости газа при постоянном давлении и постоянном объеме.
 Для нахождения
Для нахождения 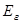 вместо твердого стержня рассмотрим цилиндрический сосуд с поршнем, создающим давление
вместо твердого стержня рассмотрим цилиндрический сосуд с поршнем, создающим давление 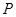 (рис. 1). Нам нужно получить для газа соотношение типа закона Гука
(рис. 1). Нам нужно получить для газа соотношение типа закона Гука
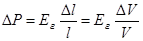 .
.
Если рассматривать давление 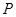 как функцию объема
как функцию объема 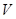 , то можно записать
, то можно записать
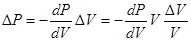 ,
, 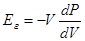 .
.
Знак “-“ стоит для того, чтобы получить 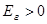 , так как для газа
, так как для газа 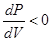 . Из уравнения (1)
. Из уравнения (1)
находим
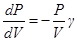 ,
, 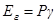 ,
, 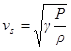 .
.
Для идеального газа с помощью уравнения Клапейрона приходим к выражению
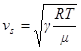 ,
,
где 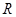 - универсальная газовая постоянная,
- универсальная газовая постоянная, 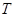 - абсолютная температура,
- абсолютная температура, 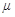 - молярная масса газа.
- молярная масса газа.
Эффект Доплера – изменение частоты при движении источника звука относительно наблюдателя.
 Пусть источник звука и приемник неподвижны. Обозначим частоту звука в этом случае через
Пусть источник звука и приемник неподвижны. Обозначим частоту звука в этом случае через 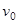 . Тогда за 1 секунду на расстоянии
. Тогда за 1 секунду на расстоянии 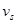 от источника уложится
от источника уложится 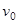 гребней (максимумов) звуковой волны (рис. 2). Если источник движется, то такое же число гребней уложится на меньшем расстоянии, равном
гребней (максимумов) звуковой волны (рис. 2). Если источник движется, то такое же число гребней уложится на меньшем расстоянии, равном 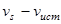 . Следовательно, приемник воспримет длину волны и частоту соответственно равные
. Следовательно, приемник воспримет длину волны и частоту соответственно равные
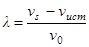 ,
, 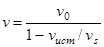 . (2)
. (2)
Таким образом, при приближении источника к приемнику ( 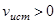 ) частота восприни-маемых колебаний возрастает, а при удалении от него (
) частота восприни-маемых колебаний возрастает, а при удалении от него ( 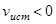 ) – уменьшается. Рассуждая аналогичным образом можно получить формулу для частоты при неподвижном источнике и движущемся приемнике
) – уменьшается. Рассуждая аналогичным образом можно получить формулу для частоты при неподвижном источнике и движущемся приемнике
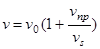 . (3)
. (3)
И в этом случае при приближении приемника к источнику частота возрастает, а при удале-нии от него понижается. Выражения (2), (3) отличаются друг от друга. Это связано с тем, что при движении источника звука среда будет возмущаться по другому по сравнению со случаем неподвижного источника.
Объединяя выражения (2), (3), можно получить формулу для частоты, когда и источник и приемник движутся вдоль соединяющей их прямой
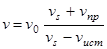 .
.
Дата добавления: 2015-08-08; просмотров: 769;
