Упругие деформации твердого тела.

Упругая деформации – после прекращения внешнего воздействия тело принимает перво-начальную форму. Если форма тела при этом изменяется, то деформация называется пластической. Рассмотрим различные типы упругих деформаций.

1. Деформации растяжения и сжатия.

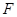Рассмотрим растяжение (сжатие) под действием силы упругого стержня, закрепленного на одном конце (рис. 1). Начальная длина стержня равна 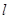, изменение длины - 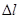,а площадь поперечного сечения - 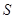. Для описания упругой деформации стержня вводятся следующие величины.

Относительное удлинение: 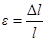( 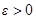- растяже-нее, 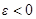- сжатие).

Нормальное напряжение: 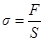, 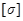= 1 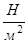= 1 Па.

Для малых ( 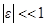) упругих деформаций растяжения и сжатия выполняется закон Гука:

.

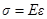Коэффициент 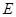называется модулем Юнга. Он зависит от свойств вещества стержня. Можно записать закон Гука в другом виде:

,

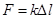где 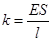- коэффициент жесткости. Он зависит от свойств вещества и от геометрических размеров стержня.

Потенциальная энергия упругой деформации растяжения (лекция 5)

,

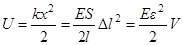где 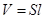- объем стержня. Важной величиной, характеризующей деформацию является плотность энергии деформации

.

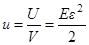При растяжения стержня радиуса 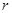на величину 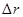изменяется также поперечный размер стержня. Из опыта следует, что для упругих деформаций

.

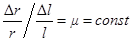Постоянная величина 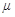называется коэффициентом Пуассона. Она определяется свойствами вещества стержня.

2. Деформация сдвига.

В этом случае внешняя сила приложена по касательной к одной из поверхностей тела имеющего форму параллелепипеда, закрепленного на противоположной грани (рис. 2). В этом случае происходит сдвиг верхней грани на расстояние 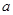и соответствующий поворот вертикального ребра на угол 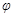. Для описания такой деформации вводят понятия относительного сдвига и тангенциального напряжения:

, .

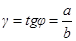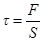Закон Гука для деформации сдвига (при ) имеет вид:

,

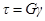где 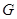- модуль сдвига, зависящий от свойств вещества твердого тела.

При перемещении верхней грани тела на расстояние 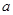сила 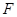совершает полную работу 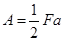, так как перемещение нижних слоев линейно спадает до нуля. Тогда потенциаль-ная энергия деформации сдвига

.

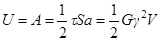Следовательно, плотность энергии деформации сдвига

.

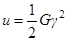Рассмотренные два вида деформаций относятся к однородным деформациям. Неоднородныедеформации представляют собой совокупность однородных деформаций, имеющих разную величину в разных точках тела. Рассмотрим две такие деформации.

3. Деформация кручения.

Рассмотрим цилиндрический стержень радиуса 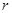, закрепленный на верхнем конце, к нижнему концу которого приложена пара сил 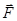и 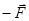(рис. 3). При этом произойдет поворот начального положения радиуса нижнего основания на угол 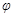. При 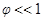имеет место закон Гука для деформации кручения:

,

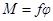где 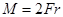- момент пары сил, 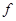- модуль кручения стержня, зависящий от материала стержня и его размеров. Если мысленно разделить стержень на тонкие цилиндрические трубки, то деформацию кручения можно представить в виде набора деформаций сдвига для узких вертикальных слоев, из которых состоит каждая из трубок. Это приводит к тому, что модуль кручения пропорционален модулю сдвига.

4. Деформация изгиба.

Рассмотрим стержень, лежащий на двух опорах, прогнувшийся под действием силы тяжести (рис. 4). При этом центральная линия, отмеченная пунктиром не изменяет своей длины. Поэтому ее называют нейтральной линией. Слои выше центральной линии сжимаются, а ниже – удлиняются. Таким образом, деформация изгиба представляет собой совокупность деформаций растяжения и сжатия. Точка 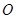, отстоящая от центральной линии на расстоянии радиуса кривизны 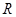называется осью изгиба.

Закон Гука для деформации изгиба имеет вид:

,

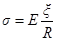где 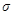- нормальное напряжение вдоль слоя, отстоящего от нейтральной линии на рассто-янии 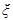. Напряжение вдоль нейтральной линии равно нулю. По этой причине нет необхо-димости использовать сплошные стержни для повышения прочности. Можно использовать более легкие профили типа швеллеров, у которых осевая часть имеет меньший поперечный размер (рис. 5).