Дифракционная решетка как спектральный прибор.

Дифракционная решетка является важнейшим спектральным прибором, предназначенным для разложения света в спектр и измерения длин волн. Из формулы (3.9.4), определяющей направления на главные фраунгоферовы максимумы, видно, что эти направления 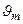зависят от длины световой волны l (за исключением максимума нулевого порядка, m = 0). Поэтому решетка в каждом порядке m ¹ 0 разложит падающий на нее свет в спектр различных порядков. Причем наибольшее отклонение в каждом порядке испытывает красная часть спектра (более длинноволновая).

Основными характеристиками любого спектрального прибора являются угловая дисперсия, разрешающая способность и область дисперсии.

1.Угловая дисперсия D характеризует степень пространственного (углового) разделения волн с различными длинами l. По определению,

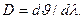(3.9.10)

где 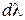- разность длин волн, дающих максимум данного порядка, - разность углов под которыми эти максимумы наблюдаются.

Дифференцируя формулу (3.9.4) при данном m находим для решетки 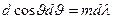, откуда

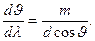(3.9.11)

Видно, что для заданного порядка m спектра угловая дисперсия тем больше, чем меньше период d решетки. Кроме того, 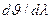растет с увеличением угла дифракции .

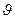2. Разрешающая способность R. По определению,

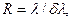(3.9.12)

где 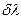— наименьшая разность длин волн спектральных линий, при которой эти линии воспринимаются еще раздельно, т. е. разрешаются. Величина R не может быть по ряду причин определена точно, а лишь ориентировочно (условно). Такой условный критерий был предложен Рэлеем.

Согласно критерию Рэлея, спектральные линии с разными длинами волн, но одинаковой интенсивности, Рис.3.9.8.

считаются разрешенными, если главный максимум одной спектральной линии совпадает с первым минимумом другой (рис.3.9.8). В этом случае между двумя максимумами возникает провал, составляющий около 20% от интенсивности в максимумах, и линии еще воспринимаются раздельно.

Итак, согласно критерию Рэлея и формуле (3.9.9), необходимо, чтобы максимум m-го порядка (m’ = mN) линии с длиной волны l + dl (рис.3.9.8) совпадал по направлению с первым минимумом линии l (m’ = mN + 1), т. е.

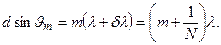
Отсюда следует, что

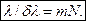(3.9.13)

Это и есть искомая формула для разрешающей способности дифракционной решетки. Данная формула дает верхний предел разрешающей способности. Она справедлива при выполнении следующих условий:

1. Интенсивность обоих максимумов должна быть одинаковой.

2. Расширение линий должно быть обусловлено только дифракцией.

3. Необходимо, чтобы падающий на решетку свет имел ширину когерентности, превышающую размер решетки. Только в этом случае все N штрихов решетки будут “работать” согласованно (когерентно), и мы достигнем желаемого результата.

Для повышения разрешающей способности спектральных приборов можно, как показывает формула (3.9.13), либо увеличивать число N когерентных пучков, либо повышать порядок интерференции m. Первое используется в дифракционных решетках (число N доходит до 200 000), второе — в интерференционных спектральных приборах (например, в интерферометре Фабри—Перо число N интерферирующих волн невелико, порядка нескольких десятков, а порядки интерференции m ~ 10⁶ и более).

3. Область дисперсииDl — это ширина спектрального интервала, при которой еще нет перекрытия спектров соседних порядков. Если спектры соседних порядков перекрываются, то спектральный аппарат становится непригодным для исследования соответствующего участка спектра.

Длинноволновый конец спектра m-го порядка совпадает с коротковолновым концом спектра (m + 1)-го порядка, если m(l + Dl) = (m + 1) l, откуда следует, что область дисперсии

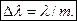(3.9.14)

Значит, область дисперсии Dl обратно пропорциональна порядку спектра т. При работе со спектрами низких порядков (обычно второго или третьего) дифракционная решетка пригодна для исследования излучения, занимающего достаточно широкий спектральный интервал.

Дифракция на двумерных и трехмерных решетках.

Двумерной решеткой называется структура, свойства которой периодически меняются в двух направлениях. Примером могут служить две скрещенные одномерные решетки, т.е. наложенные одна на другую под некоторым углом. Дифракционная картина от такой структуры может быть получена путем наложения дифракционных картин от соответствующих одномерных решеток.

Трехмерные, пространственные решетки обладают периодичностью в трех различных направлениях. Они играют важную роль в физике рентгеновских лучей. Дифракцию рентгеновских лучей на оптических дифракционных решетках получить нельзя, так как длина волны рентгеновского излучения имеет порядок 0,1нм, т.е. значительно меньше ширины щели оптической решетки. Дифракцию рентгеновских лучей можно наблюдать, если использовать кристаллическую структуру, как естественную периодическую пространственную решетку. В этом случае картина получается весьма сложной. Однако, ее можно использовать как для изучения спектрального состава излучения (если известны параметры кристалла), так и для определения характеристик кристалла (если известна длина волны излучения.

Голография.

Голография (от греческого холос – полный, графо – пишу) – способ получения объемных изображений предметов на фотопластинке при помощи когерентного излучения.

При освещении предмета от него распространяется рассеянная волна. Эта волна несет полную информацию о форме и других свойствах предмета. Попадая в глаз или объектив фотоаппарата, она образует на сетчатке или фотопластинке изображение. По степени почернения фотопластинки можно судить об амплитуде рассеянной волны. Таким образом, пластинка в этом случае сохраняет информацию только об амплитуде волны. Мы получаем плоское изображение. Для восстановления волнового поля в полном объеме (объемного изображения) этой информации недостаточно. Нужна еще информация о фазе, которую пластинка не содержит.

В 1947году английский физик и инженер Д.Габор показал, что необходимую информацию о фазе можно получить и записать на той же фотопластинке, если осветить ее вторым пучком от того же когерентного источника и заставить его интерферировать с пучком, рассеянным предметом.

Голограмма фиксирует не само изображение предмета, а структуру отраженной от него световой волны (амплитуду и фазу). Для получения голограммы необходимо, чтобы на фотопластинку одновременно попали два когерентных световых пучка: предметный, отраженный от снимаемого объекта, и опорный – приходящий непосредственно от источника. Свет обоих пучков интерферирует, создавая на пластинке чередование темных и светлых интерференционных полос. Рис.3.9.9.

Принципиальная схема устройства для записи голограммы приведена на рис.3.9.9. В этой схеме луч лазера делится специальным устройством на два. После этого лучи с помощью линз расширяются и с помощью зеркал направляются на объект и фотопластинку. Свет обоих пучков интерферирует, создавая на пластинке чередование темных и светлых полос. На экспонированной таким образом и проявленной пластинке отсутствует какое-либо изображение. Однако его в зашифрованном виде содержит система интерференционных полос. Если голограмму просветить, как диапозитив, лазерным светом той же частоты, что была использована при записи, возникнет «восстановленная голограмма» - объемное изображение предмета, словно висящее в пространстве. Меняя точку наблюдения, можно заглянуть за предметы на первом плане и увидеть детали, ранее скрытые от взгляда. Свет, проходя сквозь систему полос голограммы, дифрагирует и воспроизводит волновой фронт, исходивший от снятого предмета. Аналогичным образом лазерный луч, пропущенный через маленькое отверстие, дает на фотопластинке, поставленной за отверстием систему колец (дифракция Френеля). А световой пучок, проходящий сквозь такую пластинку, сойдется в точку. Таким образом, система колец, полученная при дифракции Френеля представляет собой простейшую голограмму – голограмму точки.

ЭЛЕМЕНТЫ КВАНТОВОЙ ФИЗИКИ.