Дифракция Фраунгофера от щели. Дифракционная решетка. Голография.
Дифракция Фраунгофера от щели.
Соответствующий расчет и здесь будет проведен с помощью принципа Гюйгенса—Френеля.
 Пусть на бесконечно длинную щель ширины b (длина щели много больше ее ширины) падает нормально плоская волна. Расположим за щелью собирающую линзу, а в ее фокальной плоскости экран (рис.3.9.1). Когда фронт волны совместится с плоскостью щели, мы можем полагать, что в щели находятся вторичные источники. Лучи от этих источников, падающие на линзу параллельным пучком, она соберет в одной точке на экране. Таким образом, в каждой точке экрана картину создают лучи, идущие от вторичных источников параллельным пучком. Поэтому эту картину Рис.3.9.1.
Пусть на бесконечно длинную щель ширины b (длина щели много больше ее ширины) падает нормально плоская волна. Расположим за щелью собирающую линзу, а в ее фокальной плоскости экран (рис.3.9.1). Когда фронт волны совместится с плоскостью щели, мы можем полагать, что в щели находятся вторичные источники. Лучи от этих источников, падающие на линзу параллельным пучком, она соберет в одной точке на экране. Таким образом, в каждой точке экрана картину создают лучи, идущие от вторичных источников параллельным пучком. Поэтому эту картину Рис.3.9.1.
называют иногда дифракцией в параллельных лучах. (Такую же
картину мы получили бы, если бы экран располагался бесконечно далеко от щели).

 Разобьем мысленно открытую часть волновой поверхности на очень узкие одинаковые по ширине зоны-полоски, параллельные прямолинейным краям щели. Суммирование вторичных волн проведем с помощью векторной диаграммы (рис.3.9.2).Колебания, приходящие в точку P от каждой такой зоны-полоски имеют одинаковую амплитуду dA. При Рис.3.9.2.
Разобьем мысленно открытую часть волновой поверхности на очень узкие одинаковые по ширине зоны-полоски, параллельные прямолинейным краям щели. Суммирование вторичных волн проведем с помощью векторной диаграммы (рис.3.9.2).Колебания, приходящие в точку P от каждой такой зоны-полоски имеют одинаковую амплитуду dA. При Рис.3.9.2.
этом разность фаз между колебаниями,
приходящими в точку P от соседних зон-полосок,
будет одинакова (проходя через линзу, лучи не приобретают дополнительной разности фаз).Отсюда следует, что при графическом изображении мы получим цепочку векторов dA, одинаковых по модулю и повернутых относительно друг друга на один и тот же угол (рис.3.9.2а). Результирующая амплитуда изобразится вектором A — хордой дуги окружности с центром в точке C.
Заметим, что для точки P0 эта цепочка образует прямую, что соответствует максимуму интенсивности.
Если разность хода крайних лучей (рис.3.9.1) составляет D = l, то их разность фаз d = 2π, цепочка оказывается замкнутой и амплитуда результирующего колебания обращается в нуль (рис.3.9.2б). Это первый минимум дифракционной картины, представляющей собой симметричную относительно середины систему чередующихся светлых и темных полос, параллельных щели.
Результирующая амплитуда обращается в нуль и тогда, когда разность фаз от крайних элементов щели равна 2πm, где m = 1, 2,... Цепочка при этом замыкается после m оборотов, практически не меняя своей длины A0, поскольку угол дифракции обычно достаточно мал.
Разность фаз d связана с разностью хода D соотношением 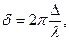
где l — длина волны света.
Так как для крайних лучей D = bsin 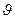 (рис.3.9.1) и в минимуме d = 2πm, то из этих трех равенств следует условие для минимумов:
(рис.3.9.1) и в минимуме d = 2πm, то из этих трех равенств следует условие для минимумов:
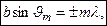 m = 1, 2, … (3.9.1)
m = 1, 2, … (3.9.1)
Заметим, что m ¹ 0, поскольку при m = 0 образуется максимум (цепочка векторов становится прямой).
Из этой формулы видно, что уменьшение ширины b щели приводит к расширению дифракционной картины.
Количество минимумов интенсивности определяется отношением ширины щели к длине волны. Из (3.9.1) следует 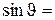 ± m
± m 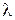 /b. Модуль
/b. Модуль 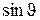 не может превысить единицу. Поэтому наибольший порядок минимума
не может превысить единицу. Поэтому наибольший порядок минимума
m ≤ b/ 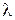 (3.9.2)
(3.9.2)
Таким образом, при ширине щели, меньшей длины волны, минимумы вообще не возникают. В этом случае интенсивность света монотонно убывает от середины картины к ее краям.
С другой стороны, если щель очень широкая, как видно из (3.9.1), минимумы будут располагаться очень близко друг от друга, так что максимумы, располагающиеся между ними, сольются и мы получим геометрическое изображение щели (дифракция не наблюдается). Поэтому в приведенном примере мы наблюдаем дифракционную картину лишь вдоль одной координаты в направлении ширины щели
 График зависимости I от sin
График зависимости I от sin 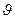 показан на рис.3.9.3. Расчеты показывают, что интенсивность второго максимума составляет около 4% от интенсивности центрального, поэтому можно считать, что практически весь световой поток, проходящий через щель, сосредоточен в первом (центральном) максимуме, угловая полуширина которого равна l/b.
показан на рис.3.9.3. Расчеты показывают, что интенсивность второго максимума составляет около 4% от интенсивности центрального, поэтому можно считать, что практически весь световой поток, проходящий через щель, сосредоточен в первом (центральном) максимуме, угловая полуширина которого равна l/b.
Отметим еще раз, что в середине симметричной Рис.3.9.3.
дифракционной картины, состоящей из чередующихся
светлых и темных полос, при дифракции Фраунгофера всегда образуется максимум освещенности (в отличие от френелевой дифракции, где центральная полоса может быть как светлой, так и темной).
Если плоская световая волна падает на щель наклонно под углом 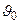 к нормали, то разность хода между колебаниями, распространяющимися от краев щели под углом
к нормали, то разность хода между колебаниями, распространяющимися от краев щели под углом 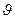 к нормали, будет равна
к нормали, будет равна 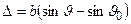 . Это при условии, что оба угла
. Это при условии, что оба угла 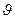 и
и 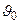 отсчитываются от нормали в одну сторону — по или против часовой стрелки.
отсчитываются от нормали в одну сторону — по или против часовой стрелки.
Условие дифракционных минимумов в данном случае принимает вид

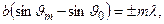 (3.9.3)
(3.9.3)
Центральный максимум (m = 0) будет расположен под углом 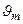 =
= 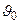 , т. е. в направлении падающей волны, и дифракционная картина будет несимметрична относительно центральной светлой полосы.
, т. е. в направлении падающей волны, и дифракционная картина будет несимметрична относительно центральной светлой полосы.
Дата добавления: 2015-08-08; просмотров: 1225;
